
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Пространства носителей
|
|
` В линейной алгебре рассматриваются отображения конечномерных векторных пространств. Но во многих случаях, например при решении дифференциальных или интегральных уравнений, возникают отображения бесконечномерных векторных пространств, элементы которых представляются уже не конечными линейными комбинациями, а рядами. Поэтому центральное понятие в бесконечномерном случае 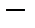 сходимость последовательности элементов пространства. Чтобы его ввести, нужно каким-то образом наделить пространство способом измерения расстояния между точками, а сами точки
сходимость последовательности элементов пространства. Чтобы его ввести, нужно каким-то образом наделить пространство способом измерения расстояния между точками, а сами точки  числовыми характеристиками. В конечномерных пространствах из фундаментальности последовательности следует сходимость и наоборот
числовыми характеристиками. В конечномерных пространствах из фундаментальности последовательности следует сходимость и наоборот 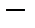 критерий полноты. В бесконечномерных пространствах из фундаментальности последовательности сходимость может не следовать. Поэтому полнота
критерий полноты. В бесконечномерных пространствах из фундаментальности последовательности сходимость может не следовать. Поэтому полнота 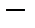 это ключевой атрибут пространства.
это ключевой атрибут пространства.
Пространство в математике 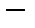 это контекстно определяемое понятие.
это контекстно определяемое понятие.
Определение. В под пространством в функциональном анализе понимают пару  , где
, где 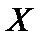
 носитель пространства, некоторое множество, которое может быть как наделено определённой (линейной) структурой, так и нет, а
носитель пространства, некоторое множество, которое может быть как наделено определённой (линейной) структурой, так и нет, а 
 заданный на элементах носителя функционал, позволяющий ввести понятие сходимости последовательности элементов пространства. На носителях
заданный на элементах носителя функционал, позволяющий ввести понятие сходимости последовательности элементов пространства. На носителях 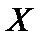 , не наделённых линейной структурой, можно ввести метрику, свойства которой являются обобщением свойств расстояния между элементами
, не наделённых линейной структурой, можно ввести метрику, свойства которой являются обобщением свойств расстояния между элементами 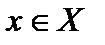 в обычном геометрическом пространстве и построить таким образом метрические пространства. Обобщениемметрическихпространств являются топологические пространства. Любое метрическое пространство
в обычном геометрическом пространстве и построить таким образом метрические пространства. Обобщениемметрическихпространств являются топологические пространства. Любое метрическое пространство  топологическое, обратное, вообще говоря, неверно. На носителях
топологическое, обратное, вообще говоря, неверно. На носителях 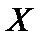 , наделённых линейной структурой, можно ввести как метрику, так и норму (длину) векторов, свойства которой являются обобщением свойств длины векторов в обычном геометрическом пространстве и построить таким образом нормированные пространства. Нормированные пространства всегда метрические и соответственно, топологические. Обратное, вообще говоря, неверно. Это такие пространства, как эвклидовы, гильбертовы и банаховы. Эвклидово пространство
, наделённых линейной структурой, можно ввести как метрику, так и норму (длину) векторов, свойства которой являются обобщением свойств длины векторов в обычном геометрическом пространстве и построить таким образом нормированные пространства. Нормированные пространства всегда метрические и соответственно, топологические. Обратное, вообще говоря, неверно. Это такие пространства, как эвклидовы, гильбертовы и банаховы. Эвклидово пространство  это нормированное пространство, где норма вводится через скалярное произведение. Иногда разделяютэвклидовы пространства на собственно эвклидовы (построенные над полем действительных чисел
это нормированное пространство, где норма вводится через скалярное произведение. Иногда разделяютэвклидовы пространства на собственно эвклидовы (построенные над полем действительных чисел  ) и унитарные (построенные над полем комплексных чисел
) и унитарные (построенные над полем комплексных чисел  ). Часто бесконечномерныеэвклидовы пространства называют предгильбертовыми, потому, что гильбертовы пространства
). Часто бесконечномерныеэвклидовы пространства называют предгильбертовыми, потому, что гильбертовы пространства 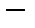 это полные эвклидовы пространства. Банаховы пространства
это полные эвклидовы пространства. Банаховы пространства 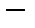 это полные нормированные пространства. То есть гильбертовы пространства
это полные нормированные пространства. То есть гильбертовы пространства 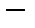 это банаховы пространства, где норма вводится через скалярное произведение. Наиболее общими пространствами, фигурирующими в функциональном анализе являются линейные топологические пространства, то есть линейные пространства Х над полем комплексных чисел
это банаховы пространства, где норма вводится через скалярное произведение. Наиболее общими пространствами, фигурирующими в функциональном анализе являются линейные топологические пространства, то есть линейные пространства Х над полем комплексных чисел  или действительных чисел
или действительных чисел  , которые одновременно являются и и топологическими пространствами, причём линейные операции непрерывны в рассматриваемой топологии. Соотношения между бесконечномерными пространствами отображены на рисунке.
, которые одновременно являются и и топологическими пространствами, причём линейные операции непрерывны в рассматриваемой топологии. Соотношения между бесконечномерными пространствами отображены на рисунке.
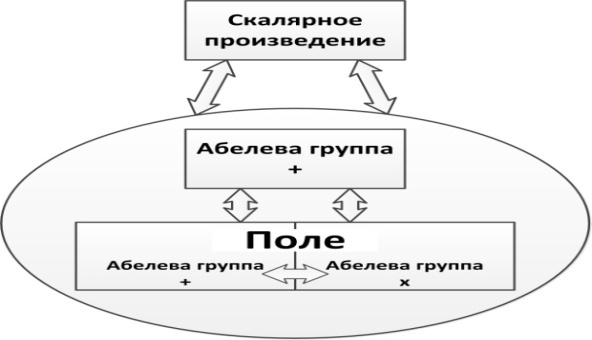
Определение. Линейной структурой 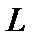 (линейным пространством, векторным пространством) называют абелеву аддитивную группу (её элементы
(линейным пространством, векторным пространством) называют абелеву аддитивную группу (её элементы  называют векторами), определённую над полем произвольной природы (элементы поля называют скалярами
называют векторами), определённую над полем произвольной природы (элементы поля называют скалярами 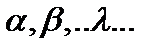 ), причём
), причём 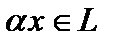 , а естественное согласование между группой и полем обеспечивается аксиомами дистрибутивности:
, а естественное согласование между группой и полем обеспечивается аксиомами дистрибутивности:  , ассоциативности по элементам поля
, ассоциативности по элементам поля 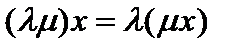 и унитарности
и унитарности  . (Символом 1 обозначен нейтральный элемент поля по умножению). Поле вещественных чисел
. (Символом 1 обозначен нейтральный элемент поля по умножению). Поле вещественных чисел  и поле комплексных чисел
и поле комплексных чисел  называют основными полями, полагая, что поле
называют основными полями, полагая, что поле  стандартно вложено в поле
стандартно вложено в поле  . Если основное поле любое, то его обозначают буквой
. Если основное поле любое, то его обозначают буквой  . То есть линейная структура
. То есть линейная структура  это четвёрка
это четвёрка  .
.

Определение 1. Пусть задана линейная структура  , где
, где  , поле
, поле  совпадает или с полем действительных чисел
совпадает или с полем действительных чисел  или с полем комплексных чисел
или с полем комплексных чисел  . Говорят, что на линейной структуре
. Говорят, что на линейной структуре  задано скалярное произведение
задано скалярное произведение  , любым элементам носителя
, любым элементам носителя 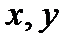 ставится в соответствие действительное или комплексное число, удовлетворяющее аксиомам (легко доказываемым для обычных геометрических векторов): 1)
ставится в соответствие действительное или комплексное число, удовлетворяющее аксиомам (легко доказываемым для обычных геометрических векторов): 1) 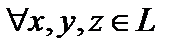 и
и 
 (линейность по первому аргументу); 2)
(линейность по первому аргументу); 2) 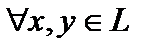
 где черта означает комплексное сопряжение (эрмитова симметричность); 3)
где черта означает комплексное сопряжение (эрмитова симметричность); 3)  ,причем
,причем 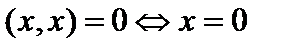 .
.
Комментарий. В определении мы абстрагируемся не только от природы изучаемых элементов и конкретного вида правил образования суммы элементов и произведения элемента на действительное число, но и от конкретного вида правила образования скалярного произведения двух элементов. Важно лишь, чтобы указанные правила удовлетворяли аксиомам. Бесконечномерныеэвклидовы пространства часто называют предгильбертовыми. В действительном эвклидовом пространствескалярное произведение  коммутативно, то есть
коммутативно, то есть  и линейно и по второму аргументу. Сложнее с комплексным эвклидовом пространством. Здесь
и линейно и по второму аргументу. Сложнее с комплексным эвклидовом пространством. Здесь  .
.
Определение 2. Эвклидовой нормой элемента 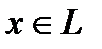 называют
называют  (как аналог длины вектора).
(как аналог длины вектора).
Пример. На множестве непрерывных функций, заданных на сегменте 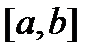 , определим скалярное произведение
, определим скалярное произведение 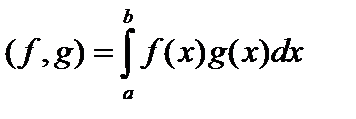 . Покажем, что это
. Покажем, что это  скалярное произведение.
скалярное произведение.
 Из свойств интеграла очевидно выполнение первых двух аксиом. Покажем унитарность. По теореме о среднем
Из свойств интеграла очевидно выполнение первых двух аксиом. Покажем унитарность. По теореме о среднем 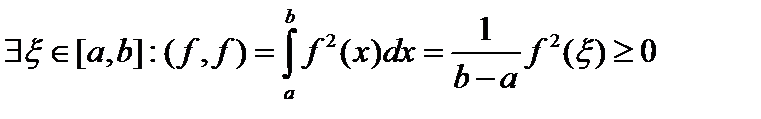 . Покажем, что
. Покажем, что  . Если
. Если 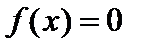 , то и
, то и  . Покажем обратное. Пусть
. Покажем обратное. Пусть  . Покажем, что
. Покажем, что 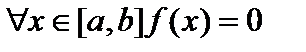 .
.  . Пусть
. Пусть  . Тогда по теореме о сохранении знака непрерывной функции
. Тогда по теореме о сохранении знака непрерывной функции  . Но тогда
. Но тогда  . Эвклидова норма элементов в пространстве непрерывных функций
. Эвклидова норма элементов в пространстве непрерывных функций  .
. 
Комментарий. Скалярное произведение на множестве непрерывных функций, заданных на сегменте 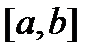 , можно определить, например, как
, можно определить, например, как  или как
или как  . Так как скалярное произведение можно ввести различными способами, то и нормы тоже отличаются между собой (удава можно мерить и мартышками и попугаями).
. Так как скалярное произведение можно ввести различными способами, то и нормы тоже отличаются между собой (удава можно мерить и мартышками и попугаями).
Заметим, что эвклидова норма  обладает очевидными свойствами:
обладает очевидными свойствами:
1.  ;
;
2.  для любого
для любого 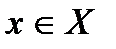 и любого числа
и любого числа  ;
;
3.  для любых
для любых 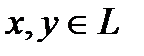 (неравенство треугольника).
(неравенство треугольника).
Неотрицательность и положительная однородность функционала  очевидны. Покажем неравенство треугольника:
очевидны. Покажем неравенство треугольника:

Приняв эти свойства за аксиомы, получим следующее
Определение 1. Говорят, что на линейной структуре  задана норма
задана норма 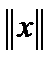 его элементов, если указан функционал, ставящий в соответствие этим элементам действительное число, удовлетворяющее аксиомам 1-3. Пара
его элементов, если указан функционал, ставящий в соответствие этим элементам действительное число, удовлетворяющее аксиомам 1-3. Пара  называется нормированным пространством.
называется нормированным пространством.
Определение 2. Полное бесконечномерное нормированное пространство называется банаховым.
Пример. Доказать, что  , где
, где 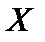 нормированное пространство, выполняется неравенство
нормированное пространство, выполняется неравенство 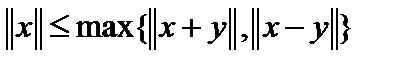 .
.
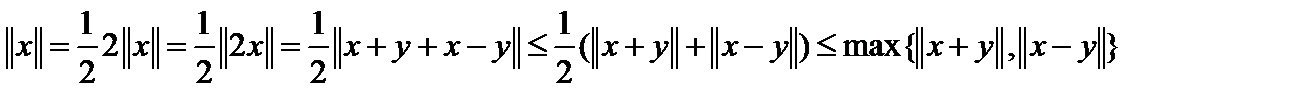 .
. 
Комментарий. 1. Ясно, что любое эвклидово пространство нормировано. Обратное, вообще говоря, неверно  нормированные пространства не обязаны быть эвклидовами.
нормированные пространства не обязаны быть эвклидовами.
2. Обратим внимание, что и гильбертовы пространства какполные бесконечномерные эвклидовы пространства и банаховы пространствакак полные бесконечномерные нормированные пространства построены на линейных структурах. Сейчас мы начнём строить пространства на произвольных носителях.
Определение. Пусть 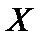 – произвольное непустое множество. Говорят, что на
– произвольное непустое множество. Говорят, что на 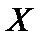 задана метрика (расстояние)
задана метрика (расстояние)  , если каждой паре элементов
, если каждой паре элементов 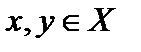 поставлено в соответствие единственное неотрицательное число
поставлено в соответствие единственное неотрицательное число 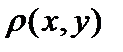 , удовлетворяющее следующим аксиомам:
, удовлетворяющее следующим аксиомам:
1)  (аксиома тождества);
(аксиома тождества);
2) 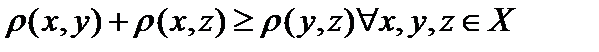 (аксиома треугольника).
(аксиома треугольника).
Таким образом, на носителе  задан неотрицательный функционал
задан неотрицательный функционал  . Пара
. Пара  , то есть множество
, то есть множество 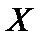 с заданной на нем метрикой
с заданной на нем метрикой  , называется метрическим пространством.
, называется метрическим пространством.
Комментарий. Из неравенства треугольника при 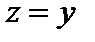 сразу получаем
сразу получаем  , а при
, а при  сразу получаем
сразу получаем  Но с другой стороны, неравенство треугольника можно записать так:
Но с другой стороны, неравенство треугольника можно записать так:  . Тогда при
. Тогда при 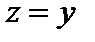 сразу получаем
сразу получаем  , то есть
, то есть  . Тогда исходная система аксиом заменяется на часто более удобную систему из трёх аксиом:
. Тогда исходная система аксиом заменяется на часто более удобную систему из трёх аксиом: 
Определение. Если  – метрическое пространство и
– метрическое пространство и  , то пара
, то пара  также будет являться метрическим пространством и называется подпространством пространства
также будет являться метрическим пространством и называется подпространством пространства  , если
, если 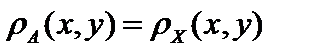 , то есть расстояние между точками
, то есть расстояние между точками 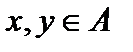 – равно расстоянию между этими точками в пространстве
– равно расстоянию между этими точками в пространстве  .
.
Комментарий. Стандартные пространства – это метрические или нормированные пространства со стандартными носителями и со стандартными метриками или нормами. В этих случаях пространства носят стандартные названия.
Date: 2015-09-03; view: 539; Нарушение авторских прав