Уравнение неразрывности жидкости

Динамика невязкой жидкости

Уравнение неразрывности жидкости

Уравнение неразрывности, или сплошности, жидкости основано на законе со­хранения массы и исходит из положения механики сплошных сред о том, что внутри движущейся жидкости не может произойти разрыв, не может установить­ся пустота.

Рисунок 17

В потоке выделим элементарный объем в форме параллелепипеда с ребрами dx, dy, dz (рис. 17). Рассмотрим изменение протекающей массы жидкости по оси х. Скорость жидкости, которая втекает в левую грань параллелепипеда, обозна­чим через и тогда скорость жидкос­ти, вытекающей из правой грани, можно выразить как .

Принимая плотность жидкости р по­стоянной, можно записать, что через левую грань за время dt прой­дет масса:

,

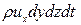а через правую:

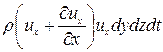
Разность этих масс составляет:

Рассматривая по аналогии изменение массы жидкости по оси у и г, запишем:

;

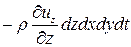
Закон сохранения массы требует, что­бы общее изменение массы, прошедшей через выбранный объем, равнялось нулю:

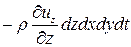=0

Отсюда следует, что

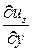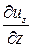+ + =0

Это выражение и называется уравне­нием неразрывности, или сплошности, в дифференциальной форме для произ­вольного движения несжимаемой жидкости.

Левая часть уравнения пред­ставляет собой скорость относительного изменения элементарного объема жидкос­ти (объемное расширение) и называется дивергенцией, или расхождением, векто­ра скорости (div ); при этом:

div =0

Из уравне­ния неразрывности следует, что при установившемся движении, количества жидкости, притекающей к элементарной струйке в начальном живом сечении и вытекающей из нее в конечном живом сечении, равны между собой и общий объем жидкости в струйке не изменяется.

Рассмотрим живые сечения 1—1 и 2—2 элементарной струйки (рис. 10) со скоростями соответственно 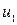и . Объемы жидкости, прошедшие через сечения 1—1 и 2—2 в единицу времени, составляют элементарные рас­ходы и 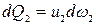. Вви­ду постоянства объема струйки 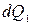= 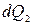и тогда:

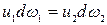
Это выражение является уравне­нием неразрывности, или сплошности, для элементарной струйки.

Для потока жидкости (рис. 17), пред­ставляющего собой совокупность эле­ментарных струек, можно записать:

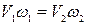
Это уравне­ние неразрывности или сплошности для потока жидкости при ус­ловии 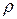=const математически выра­жает собой закон сохранения массы, открытый М. В. Ломоносовым.

Дифференциальные уравнения движения невязкой жидкости (уравнения Эйлера)

Основной задачей гидродинамики является определение значений скорости и и гидродинамиче­ского давления р. Эта задача решается методом Эйлера. При выводе дифференциальных урав­нений движения жидкость принимается невязкой (идеальной), то есть каса­тельные напряжения, характеризую­щие деформацию частиц жидкости, не учитываются. В связи с этим можно не учитывать силы трения и считать, что массовые силы и силы давления, явля­ющиеся причиной движения, определя­ются также, как и в покоящейся жидкос­ти (в гидростатике).

Отнеся компоненты уравне­ний равновесия к единице массы, получим:

Эти уравнения выражают условия рав­новесия сил. Для перехода от равновесия к движению необходимо к действующим силам прибавить силы инерции:

,

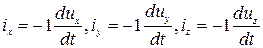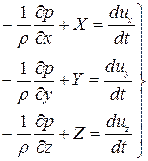
Эти уравнения были получены в 1755 г. академиком Российской Акаде­мии наук Л. Эйлером и называются диф­ференциальными уравнениями движения невязкой жидкости.

Или в развернутом виде уравнения Эй­лера для движения невязкой жидкости:

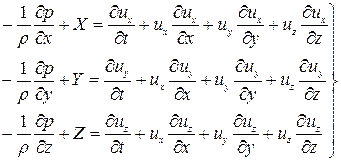
Первые составляющие левой части выражают силы гидродинамического давления, вто­рые - внешние действующие силы, а в правой части представлены силы инерции.

Полученные в таком виде дифферен­циальные уравнения Эйлера положили начало практическому изучению дви­жения жидкости. Поскольку для на­хождения четырех неизвестных и_х, и_y, и_г и 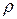недостаточно трех уравнений, то к ним прибавляют четвертое - уравнение неразрывности или сплошности движения для несжимаемой жидкос­ти.

Date: 2015-09-03; view: 568; Нарушение авторских прав