Принцип Даламбера для механической системы

Рассмотрим механическую систему, состоящую из n материальных точек. К каждой точке системы 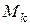в общем случае приложены равнодействующая активных сил 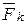, равнодействующая реакций 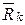и сила инерции 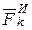. Применяя принцип Даламбера (6.4) для каждой точки системы, получим

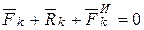. (6.5)

где k =1,2,3,…, n.

Система n уравнений (6.5) выражает принцип Даламбера для системы, который формулируют следующим образом: п ри движении механической системы активные силы, реакции связей и сила инерции образует равновесную систему сил для каждой точки системы.

Суммируя (6.5) по всем точкам системы, получим

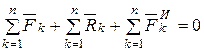, (6.6)

где 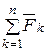- главный вектор активных сил,

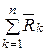- главный вектор реакций связей,

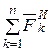- главный вектор сил инерции.

Умножая векторным способом все слагаемые выражения (6.6) на радиус-вектор точки 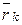, относительно произвольно выбранного центра O, получим

,

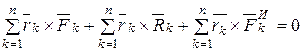или

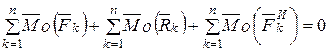, (6.7)

где 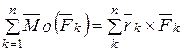- главный момент активных сил,

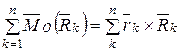- главный момент реакций связей,

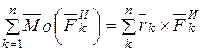- главный момент сил инерции.

Таким образом, для системы материальных точек имеем два векторных уравнения

.

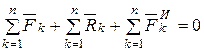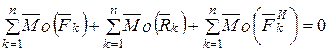Проецируя эти уравнения на оси координат, получим шесть уравнений метода кинетостатики:

;

;

;

;

.

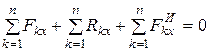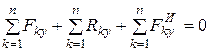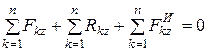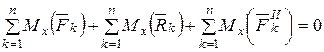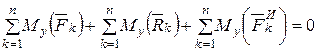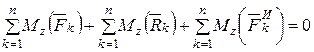Определим главный вектор и главный момент сил инерции.

Разложим главный вектор и главный момент активных сил и реакций связей на главный вектор и главный момент внешних и внутренних сил системы

,

.

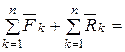
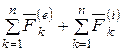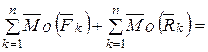
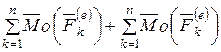Учитывая свойства внутренних сил системы (4.1) и (4.2), получим

,

.

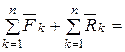
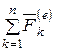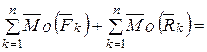
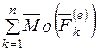Тогда уравнения (6.8) примут вид

,

.

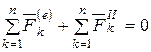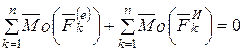Выражая главный вектор и главный момент сил инерции, получим

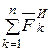
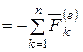, (6.10)

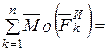
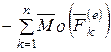. (6.11)

По теореме о движении центра масс (4.16), получим

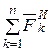
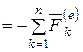
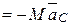, (6.12)

где 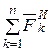- главный вектор сил инерции,

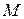- масса системы,

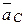- ускорение центра масс системы.

По теореме об изменении кинетического момента (4.23) получим

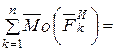
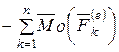
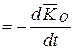, (6.13)

где 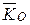- кинетический момент системы относительно центра O.

В случае вращения твердого тела вокруг неподвижной оси Oz, по формуле (4.27), получим

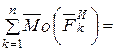
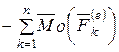
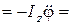
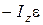, (6.13)

где 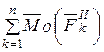- главный момент сил инерции, 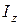- момент инерции твердого тела относительно сои вращения, 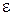- угловое ускорение тела.

Date: 2015-09-03; view: 371; Нарушение авторских прав