Движение тела, брошенного горизонтально

Если скорость 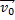направлена не вертикально, то движение тела будет криволинейным.

Рассмотрим движение тела, брошенного горизонтально с высоты h со скоростью 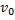(рис. 28). Сопротивлением воздуха будем пренебрегать. Для описания движения необходимо выбрать две оси координат — Ох и Оу. Начало отсчета координат совместим с начальным положением тела. Из рис.28 видно, что , , , .

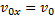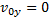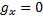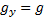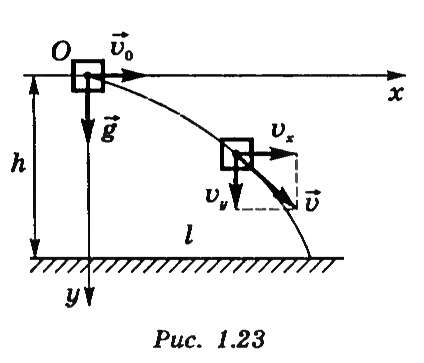
Рис.28

Тогда движение тела опишется уравнениями:

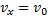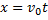, (3)

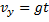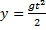, (4)

Анализ этих формул показывает, что в горизонтальном направлении скорость тела остается неизменной, т.е. тело движется равномерно. В вертикальном направлении тело движется равноускоренно с ускорением g, т.е. так же, как тело, свободно падающее без начальной скорости. Найдем уравнение траектории. Для этого из уравнения (3) найдем время

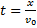и, подставив его значение в формулу (4), получим: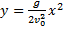

Это уравнение параболы. Следовательно, тело, брошенное горизонтально, движется по параболе. Скорость тела в любой момент времени направлена по касательной к параболе (см. рис. 28). Модуль скорости можно рассчитать по теореме Пифагора:

Зная высоту h, с которой брошено тело, можно найти время t1, через которое тело упадет на землю. В этот момент координата у равна высоте у₁=h. Из уравнения (4) находим: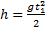

Отсюда

Формула (5) определяет время полета тела. За это время тело пройдет в горизонтальном направлении расстояние l, которое называют дальностью полета и которое можно найти на основании формулы (3), учитывая, что l =x₁. Следовательно, 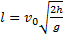— дальность полета тела. Модуль скорости тела в этот момент .

Date: 2015-09-03; view: 845; Нарушение авторских прав