
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Механическое движение. Пространство и время в механикеи Ньютона. Кинематическое уравнение движения. Радиус-вектор. Траектория. Путь. Перемещение
|
|
КИНЕМАТИКА
МЕХАНИЧЕСКОЕ ДВИЖЕНИЕ. ПРОСТРАНСТВО И ВРЕМЯ В МЕХАНИКЕИ НЬЮТОНА. КИНЕМАТИЧЕСКОЕ УРАВНЕНИЕ ДВИЖЕНИЯ. РАДИУС-ВЕКТОР. ТРАЕКТОРИЯ. ПУТЬ. ПЕРЕМЕЩЕНИЕ
Механическим движением называется изменение взаимного расположения тел или их частей.
Раздел физики, занимающийся изучением закономерностей механического движения и взаимодействия тел, называется механикой. При этом под механическим действием на тело понимают такое воздействие со стороны других тел, которое приводит к изменению состояния механического движения рассматриваемого тела или к его деформации, т.е. к изменению взаимного расположения его частей.
Классическая механика рассматривает движение макроскопических тел, скорости которых много меньше скорости света в вакууме с= 3×10 м/с. Основы классической механики были разработаны И.Ньютоном, поэтому ее обычно называют ньютоновской механикой.
Решая ту или иную конкретную задачу механики, всегда выделяют из множества тел только те, которые играют в данной задаче существенную роль. Эта совокупность тел называется механической системой.
Мы будем изучать два основных раздела классической механики: кинематику и динамику.
Кинематика описывает механическое движение тел безотносительно к причинам, вызвавшим движение. Динамика занимается исследованием влияния взаимодействия тел на их механическое движение.
В механике для описания реальных тел пользуются в зависимости от условий конкретной задачи различными упрощенными моделями: материальная точка, абсолютно твердое тело, абсолютно упругое тело, абсолютно неупругое тело и т.д. Выбор той или иной модели нужно производить так, чтобы учесть все существенные особенности поведения реального тела в данной задаче и отбросить все второстепенные, неоправданно усложняющие решение.
Материальной точкой называется тело, формой и размерами которого в данной задаче можно пренебречь.
Одно и то же тело в одних задачах можно считать материальной точкой, а в других – нельзя. Например, рассматривая движение Земли по орбите вокруг Солнца, ее можно считать материальной точкой, т.к. размеры Земли много меньше радиуса орбиты. В то же время при рассмотрении движения тел по Земле ее уже нельзя считать материальной точкой. Любое протяженное тело или систему тел, образующих механическую систему, можно представить как систему материальных точек. Для этого все тела системы разбивают на такие части, размерами каждой из которых можно пренебречь в сравнении с размерами самих тел.
Абсолютно твердым называется тело, деформацией которого можно пренебречь. При любых взаимодействиях расстояния между любыми двумя точками абсолютно твердого тела остаются неизменными.
Все тела существуют в пространстве и во времени. Любое тело имеет объем, т.е. пространственную протяженность. Пространство и время являются основными категориями движения материи. Пространство определяет порядок сосуществования отдельных объектов. Время выражает порядок смены состояний, составляющих любое движение. Оно служит мерой длительности процесса. Пространство и время служат основой конструирования теоретических моделей, интерпретирующих экспериментальные данные, и имеют решающее значение при построении физической картины мира.
В механике Ньютона существует понятие абсолютного пространства и абсолютного времени, которые не зависят друг от друга и от существующих в них материальных объектов и протекающих процессов. Длина масштабов и времени считаются абсолютными. Любой масштаб (расстояние) считается одинаковым во всех системах отсчета, т.е. не зависит от движения. То же касается и времени.
Положение тела в пространстве определяется только относительно каких-либо других тел. Для однозначного определения положения исследуемого тела в произвольный момент времени необходимо выбрать систему отсчета.
 Абсолютно твердое тело и жестко связанную с ним систему координат, снабженную часами, используемую для определения положения материальной точки в пространстве в любой момент времени, называют системой отсчета.
Абсолютно твердое тело и жестко связанную с ним систему координат, снабженную часами, используемую для определения положения материальной точки в пространстве в любой момент времени, называют системой отсчета.
При этом под часами подразумевается любое устройство, измеряющее промежутки времени между событиями. Начало отсчета времени выбирается произвольно. Абсолютно твердое тело, с которым связывают систему координат, называют телом отсчета.
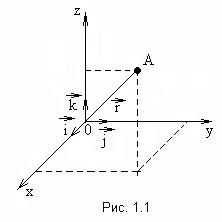
В качестве системы координат в классической механике наиболее часто используется прямоугольная декартова система координат, имеющая ортонормированный базис, заданный ортами 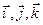 (рис.1.1). Положение точки A относительно этой системы координат задают радиус-вектором
(рис.1.1). Положение точки A относительно этой системы координат задают радиус-вектором  (это вектор, проведенный из начала координат в данную точку),
(это вектор, проведенный из начала координат в данную точку),
 (1.1)
(1.1)
либо тремя координатами x, y, z.
При движении точки A ее координаты и радиус-вектор изменяются с течением времени, поэтому для задания закона движения этой точки необходимо указать три непрерывные и однозначные функции времени 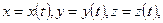
либо векторную функцию
 (1.2)
(1.2)
 Выражения вида (1.2) называются кинематическими уравнениями движения.
Выражения вида (1.2) называются кинематическими уравнениями движения.
Траекторией называется линия, которую описывает в пространстве движущаяся точка. В зависимости от формы траектории различают прямолинейное и криволинейное движение. Движение называют плоским, если все точки траектории лежат в одной плоскости. В этом случае уравнение траектории удобно задавать в виде y = y (x).
Механическое движение тела относительно: его характер, а, следовательно, и форма траектории, зависят от выбора системы отсчета. Например, тело, свободно падающее с полки в вагоне равномерно движущегося поезда, в системе отсчета, связанной с вагоном, движется вертикально вниз, а в системе отсчета, связанной с Землей, совершает плоское движение по параболе.
 Длиной пути, пройденного точкой за некоторый промежуток времени, называется сумма длин всех участков траектории, пройденных за этот промежуток. Длина пути
Длиной пути, пройденного точкой за некоторый промежуток времени, называется сумма длин всех участков траектории, пройденных за этот промежуток. Длина пути 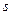 – это скалярная неотрицательная величина.
– это скалярная неотрицательная величина.
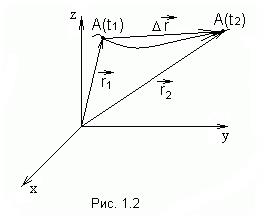
Пусть в момент времени 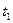 положение точки характеризовалось радиус-вектором
положение точки характеризовалось радиус-вектором  , а в момент времени
, а в момент времени 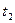 радиус-вектором
радиус-вектором 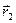 (рис.1.2). Перемещением точки за промежуток времени
(рис.1.2). Перемещением точки за промежуток времени 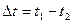 называется вектор
называется вектор  , проведенный из начального положения точки (в момент времени
, проведенный из начального положения точки (в момент времени 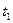 ) в ее конечное положение (в момент времени
) в ее конечное положение (в момент времени 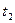 ).
).
Если точка совершает последовательно два перемещения 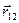 и
и  , то результирующее перемещение равно векторной сумме (рис.1.3):
, то результирующее перемещение равно векторной сумме (рис.1.3):  .
.
ОСНОВНЫЕ КИНЕМАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ КРИВОЛИНЕЙНОГО ДВИЖЕНИЯ: СКОРОСТЬ И УСКОРЕНИЕ. ФИЗИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ И ИНТЕГРАЛА. ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ ДВИЖЕНИЯ. РОЛЬ НАЧАЛЬНЫХ УСЛОВИЙ. СИСТЕМЫ КООРДИНАТ И ИХ ПРЕОБРАЗОВАНИЯ. НОРМАЛЬНОЕ И ТАНГЕНЦИАЛЬНОЕ УСКОРЕНИЕ
 В физике под скоростью понимают векторную величину, характеризующую быстроту перемещения материальной точки по траектории и направление движения в каждый момент времени. Разобьем траекторию на бесконечно малые участки длины
В физике под скоростью понимают векторную величину, характеризующую быстроту перемещения материальной точки по траектории и направление движения в каждый момент времени. Разобьем траекторию на бесконечно малые участки длины 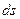 (рис.1.4), каждому из этих участков сопоставим бесконечно малое перемещение
(рис.1.4), каждому из этих участков сопоставим бесконечно малое перемещение  . Разделив это перемещение на соответствующий промежуток времени
. Разделив это перемещение на соответствующий промежуток времени 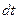 , получим мгновенную скорость в данной точке траектории:
, получим мгновенную скорость в данной точке траектории:
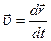 . (1.3)
. (1.3)
Таким образом, скорость есть первая производная радиус-вектора точки по времени. Перемещение  совпадает с бесконечно малым элементом траектории, следовательно вектор
совпадает с бесконечно малым элементом траектории, следовательно вектор 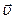 направлен по касательной к траектории (рис.1.4).
направлен по касательной к траектории (рис.1.4).
Разложив вектор скорости по базису системы координат, получаем:
 , где
, где  - проекции вектора
- проекции вектора 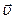 на координатные оси. Модуль вектора скорости равен
на координатные оси. Модуль вектора скорости равен  .
.
Можно показать, что модуль скорости равен производной пути по времени:

Движение называется равномерным, если вектор скорости остается постоянным по величине и направлению. В противном случае говорят о переменном движении.
В соответствии с формулой (1.3), элементарное перемещение материальной точки  . Тогда перемещение из положения 1 в положение 2 (рис.1.2) равно интегралу
. Тогда перемещение из положения 1 в положение 2 (рис.1.2) равно интегралу

Пройденный путь определяется выражением  .
.
Среднее значение модуля скорости за промежуток времени от 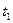 до
до 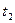 равно
равно  . Средний вектор скорости:
. Средний вектор скорости: 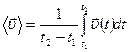 .
.
Вектор скорости можно представить в виде
 , (1.4)
, (1.4)
где 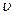 – модуль скорости,
– модуль скорости, 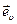 – орт вектора
– орт вектора 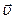 . Введем орт касательной к траектории
. Введем орт касательной к траектории 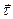 , условившись направлять его в ту же сторону, что и
, условившись направлять его в ту же сторону, что и 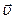 . Тогда, очевидно, орты
. Тогда, очевидно, орты 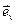 и
и 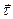 совпадут, и можно записать
совпадут, и можно записать 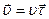
 Подставив в выражение (1.3) радиус-вектор в виде
Подставив в выражение (1.3) радиус-вектор в виде 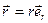 , получаем
, получаем
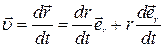 .
.
Для простоты рассуждений будем считать траекторию плоской кривой, лежащей в плоскости  (рис.1.5). В записанной формуле первая составляющая вектора скорости
(рис.1.5). В записанной формуле первая составляющая вектора скорости 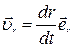 направлена вдоль радиус-вектора
направлена вдоль радиус-вектора  и характеризует быстроту изменения модуля
и характеризует быстроту изменения модуля  . Вторая составляющая равна
. Вторая составляющая равна 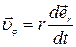 и характеризует быстроту изменения радиус-вектора по направлению.
и характеризует быстроту изменения радиус-вектора по направлению.
Из математики известно:  , где
, где  – угол между радиус-вектором и осью
– угол между радиус-вектором и осью  ,
, 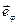 – перпендикулярный к радиус-вектору орт, направленный в сторону возрастания угла
– перпендикулярный к радиус-вектору орт, направленный в сторону возрастания угла  . Подставив
. Подставив 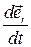 в формулу для
в формулу для 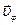 , получаем
, получаем
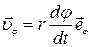 .
.
Таким образом, составляющая 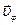 и соответствующий орт
и соответствующий орт 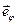 связаны с изменением угла
связаны с изменением угла  .
.
 Очевидно, что векторы
Очевидно, что векторы  и
и 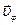 взаимно перпендикулярны, следовательно
взаимно перпендикулярны, следовательно
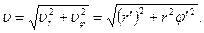
Быстрота изменения вектора скорости 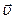 называется ускорением материальной точки и определяется производной вектора
называется ускорением материальной точки и определяется производной вектора 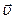 по времени:
по времени:
 . (1.5)
. (1.5)
Cпроектируем это выражение на координатные оси:  .
.
Обратная задача кинематики состоит в том, чтобы, зная зависимость от времени ускорения  материальной точки, найти зависимость скорости
материальной точки, найти зависимость скорости 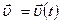 и радиус-вектора от времени
и радиус-вектора от времени  . Для получения однозначного решения этой задачи одной зависимости
. Для получения однозначного решения этой задачи одной зависимости  оказывается недостаточно. Необходимо знать еще начальные условия, т.е. скорость
оказывается недостаточно. Необходимо знать еще начальные условия, т.е. скорость  и радиус-вектор
и радиус-вектор 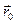 точки в момент времени, принятый за начальный.
точки в момент времени, принятый за начальный.
Рассмотрим равноускоренное движение,  . Изменение скорости точки за время t, очевидно, равно интегралу
. Изменение скорости точки за время t, очевидно, равно интегралу 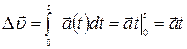 . Чтобы найти
. Чтобы найти 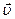 , надо знать скорость
, надо знать скорость  в начальный момент времени. Тогда
в начальный момент времени. Тогда  .
.
Изменение радиус-вектора точки за время t равно интегралу 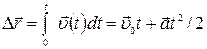 . Чтобы найти
. Чтобы найти  , надо знать радиус-вектор в начальный момент времени
, надо знать радиус-вектор в начальный момент времени 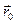 . Тогда
. Тогда 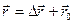 .
.
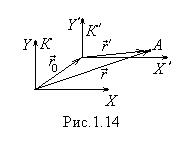 Рассмотрим две произвольные системы отсчета К и К', движущиеся определенным образом друг относительно друга. В К -системе материальная точка А имеет скорость
Рассмотрим две произвольные системы отсчета К и К', движущиеся определенным образом друг относительно друга. В К -системе материальная точка А имеет скорость 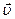 и ускорение
и ускорение  . Положение материальной точки в этой системе отсчета задано радиус-вектором
. Положение материальной точки в этой системе отсчета задано радиус-вектором  . В К' -системе скорость точки
. В К' -системе скорость точки  , ускорение
, ускорение  , радиус-вектор
, радиус-вектор 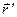 . К' -система движется относительно К - системы со скоростью
. К' -система движется относительно К - системы со скоростью  и ускорением
и ускорением  , в начальный момент времени начало отсчета К' -системы в К -системе задано радиус-вектором
, в начальный момент времени начало отсчета К' -системы в К -системе задано радиус-вектором 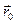 (рис.1.14). Тогда, как следует из рис.1.14,
(рис.1.14). Тогда, как следует из рис.1.14,  . За промежуток времени dt точка А совершит в К –системе перемещение
. За промежуток времени dt точка А совершит в К –системе перемещение  . Это перемещение складывается из перемещения
. Это перемещение складывается из перемещения 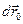 вместе с К' -системой и перемещения
вместе с К' -системой и перемещения  относительно К' -системы,
относительно К' -системы, 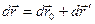 . Разделив это выражение на dt, получим формулу преобразования скорости:
. Разделив это выражение на dt, получим формулу преобразования скорости:
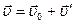 .
.
Продифференцировав по времени, находим формулу преобразования ускорения: 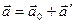 . Если К' -система движется относительно К -системы без ускорения,
. Если К' -система движется относительно К -системы без ускорения,  =0, тогда
=0, тогда  . Этот факт будет прокомментирован позднее (см.раздел Динамика).
. Этот факт будет прокомментирован позднее (см.раздел Динамика).
Подставив в формулу (1.5) выражение (1.4), получаем:  . Продифференцировав, имеем:
. Продифференцировав, имеем:  .
.
Следовательно, вектор  можно представить в виде суммы двух взаимно перпендикулярных составляющих (рис.1.6). Первая направлена по касательной к траектории и называется тангенциальным или касательным ускорением
можно представить в виде суммы двух взаимно перпендикулярных составляющих (рис.1.6). Первая направлена по касательной к траектории и называется тангенциальным или касательным ускорением
 . (1.6)
. (1.6)
Вторая составляющая направлена по 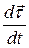 , т.е. перпендикулярно касательной, по нормали к траектории, и называется нормальным ускорением
, т.е. перпендикулярно касательной, по нормали к траектории, и называется нормальным ускорением 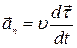 .
.
Исследуем свойства обеих составляющих, ограничившись случаем плоского движения. Модуль тангенциального ускорения, как следует из (1.6), равен  . Если
. Если 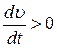 (скорость растет по величине), вектор
(скорость растет по величине), вектор 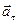 направлен в ту же сторону, что и
направлен в ту же сторону, что и 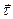 (т.е. в ту же сторону, что и
(т.е. в ту же сторону, что и 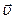 ). Если
). Если 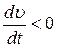 (скорость со временем уменьшается), векторы
(скорость со временем уменьшается), векторы 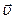 и
и 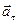 направлены противоположно. При равномерном движении
направлены противоположно. При равномерном движении 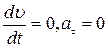 .
.
 Нормальное ускорение определяется величиной
Нормальное ускорение определяется величиной 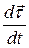 , т.е. быстротой изменения во времени направления касательной к траектории. Эта быстрота будет тем больше, чем сильнее искривлена траектория и чем быстрее перемещается частица по траектории.
, т.е. быстротой изменения во времени направления касательной к траектории. Эта быстрота будет тем больше, чем сильнее искривлена траектория и чем быстрее перемещается частица по траектории.
Степень искривления плоской кривой характеризуется кривизной С, которая определяется выражением
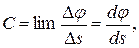
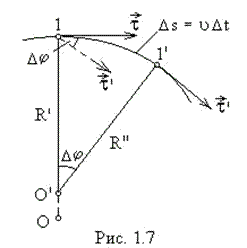
где 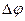 – угол между касательными к кривой в точках, отстоящих друг от друга на расстояние
– угол между касательными к кривой в точках, отстоящих друг от друга на расстояние  (рис.1.7). Таким образом, кривизна определяет скорость поворота касательной при перемещении вдоль кривой. Величина, обратная кривизне С, называется радиусом кривизны
(рис.1.7). Таким образом, кривизна определяет скорость поворота касательной при перемещении вдоль кривой. Величина, обратная кривизне С, называется радиусом кривизны  в данной точке:
в данной точке: 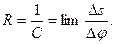
Радиус кривизны представляет собой радиус окружности, которая сливается в данном месте с кривой на бесконечно малом ее участке. Центр такой окружности называется центром кривизны для данной точки кривой.
Радиус и центр кривизны в точке 1 (рис.1.7) определим следующим образом. Возьмем вблизи точки 1 точку 1¢. Построим в этих точках касательные 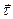 и
и  , перпендикуляры к которым пересекутся в некоторой точке О ¢. При этом для кривой, не являющейся окружностью, расстояния
, перпендикуляры к которым пересекутся в некоторой точке О ¢. При этом для кривой, не являющейся окружностью, расстояния  ¢ и
¢ и  ¢¢ несколько отличаются друг от друга. Если точку 1¢ приближать к точке 1, пересечение перпендикуляров O ¢ будет перемещаться вдоль прямой
¢¢ несколько отличаются друг от друга. Если точку 1¢ приближать к точке 1, пересечение перпендикуляров O ¢ будет перемещаться вдоль прямой  ¢ и в пределе окажется в некоторой точке О. Эта точка и будет центром кривизны для точки 1. Расстояния R ¢ и R ¢¢ будут стремиться к общему пределу
¢ и в пределе окажется в некоторой точке О. Эта точка и будет центром кривизны для точки 1. Расстояния R ¢ и R ¢¢ будут стремиться к общему пределу  , равному радиусу кривизны.
, равному радиусу кривизны.
Как известно из математики, 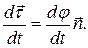 (1.7)
(1.7)
Здесь  – орт нормали к траектории, направленный в сторону поворота вектора
– орт нормали к траектории, направленный в сторону поворота вектора 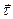 при движении частицы по траектории. Величину
при движении частицы по траектории. Величину 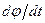 можно связать с радиусом кривизны траектории и скоростью частицы
можно связать с радиусом кривизны траектории и скоростью частицы 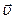 . Из рис. 1.7 следует, что
. Из рис. 1.7 следует, что 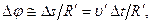 где
где 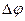 - угол поворота вектора
- угол поворота вектора 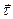 за время
за время 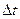 (совпадающий с углом между перпендикулярами
(совпадающий с углом между перпендикулярами  ¢ и
¢ и  ¢¢),
¢¢), 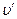 - средняя скорость на пути
- средняя скорость на пути  . Отсюда
. Отсюда 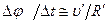 . В пределе при
. В пределе при 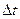 ® 0 приближенное равенство станет строгим, средняя скорость
® 0 приближенное равенство станет строгим, средняя скорость 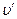 превратится в мгновенную скорость
превратится в мгновенную скорость 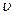 в точке 1,
в точке 1,  ¢- в радиус кривизны
¢- в радиус кривизны  . В результате получится равенство
. В результате получится равенство
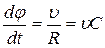 (1.8)
(1.8)
- быстрота поворота вектора скорости пропорциональна кривизне траектории и скорости перемещения частицы по траектории.
Подставив (1.7) в формулу (1.8), получим 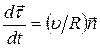 , тогда нормальное ускорение равно
, тогда нормальное ускорение равно 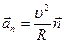 .
.
 Вектор ускорения при движении материальной точки по плоской кривой равен
Вектор ускорения при движении материальной точки по плоской кривой равен  , а его модуль
, а его модуль 
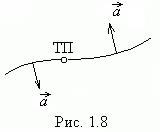
При прямолинейном движении нормальное ускорение отсутствует. Интересным является тот факт, что 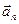 обращается в ноль в точке перегиба криволинейной траектории (точка ТП на рис.1.8). По обе стороны от этой точки векторы
обращается в ноль в точке перегиба криволинейной траектории (точка ТП на рис.1.8). По обе стороны от этой точки векторы 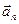 направлены в разные стороны. Вектор
направлены в разные стороны. Вектор 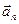 не может изменяться скачком, изменение направления на противоположное происходит плавно с обращением
не может изменяться скачком, изменение направления на противоположное происходит плавно с обращением 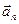 в ноль в точке перегиба.
в ноль в точке перегиба.
Если материальная точка движется с постоянными по величине скоростью и ускорением, то  , так что
, так что 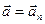 и
и 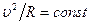 , поэтому
, поэтому 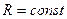 – частица движется по линии постоянной кривизны, т.е. по окружности.
– частица движется по линии постоянной кривизны, т.е. по окружности.
Date: 2015-09-03; view: 710; Нарушение авторских прав