
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Графики вариационных рядов
|
|
Для того чтобы более наглядно представить закономерность варьирования количественных признаков, вариационные ряды принято изображать в виде графиков. Так, при построении графика безынтервального вариационного ряда по оси абсцисс откладывают средние значения классов, а по оси ординат – частоты. Высоты перпендикуляров, откладываемых по оси абсцисс, соответствует частотам классов. Соединяя вершины перпендикуляров прямыми линиями, получают геометрическую фигуру в виде многоугольника, называемую полигоном распределения частот. Линия, соединяющая вершины перпендикуляров, называется вариационной кривой или кривой распределения частот вариационного ряда (рис. 2.1).
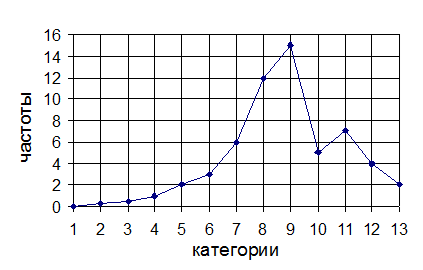 |
Рис. 2.1 Пример полигона распределения частот вариационного ряда
При построении графика интервального вариационного ряда по оси абсцисс откладывают границы классовых интервалов, а по оси ординат – частоты интервалы. В результаты получается так называемая гистограмма распределения частот (рис. 2.2).
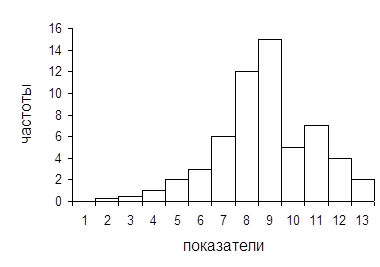 |
Рис. 2.2 Пример гистограммы распределения частот
Если из середин верхних сторон прямоугольников гистограммы опустить перпендикуляр на ось абсцисс, то гистограмма превращается в полигон распределения, а линия, соединяющая середины верхних сторон прямоугольников гистограммы, будет представлять собой вариационную кривую.
Если по оси абсцисс откладывать значения классов, а по оси ординат – накопленные частоты с последующим соединением точек прямыми линиями, получается график, называемый комулятой (см. рис. 2.3). В отличие от вариационной кривой, имеющей куполообразную форму, кумулята имеет вид S-образной кривой. Накопленные частоты находят последовательным суммированием, или кумуляцией (от лат. cumulatio – увеличение, скопление) частот в направлении от первого класса до конца вариационного ряда.
Откладывая по оси абсцисс частоты, а по оси ординат значения классов с последующим соединением геометрических точек прямыми линиями, как это показано на рис. 2.4, получают линейный график, называемый огивой.
По сравнению с эмпирическими вариационными кривыми, которые выглядят обычно в виде ломанных линий, кумулята и огива имеют более обтекаемую форму. Это особенность позволяет в ряде случаев отдавать предпочтение этим графикам перед эмпирической вариационной кривой.
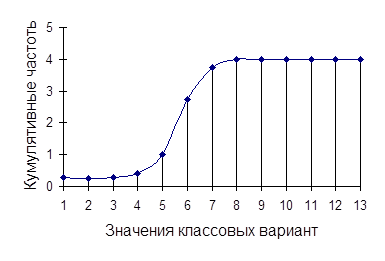 |
Рис. 2.3 Пример графика кумуляты
Центральная точка кумуляты совпадает с центром распределения совокупности, что дает возможность использовать ее при определении, например, средних доз биологически активных веществ, вызывающих эффект у 50 % подопытных индивидов. Огива позволяет сравнивать друг с другом одновременно несколько эмпирических распределений неравного объема.
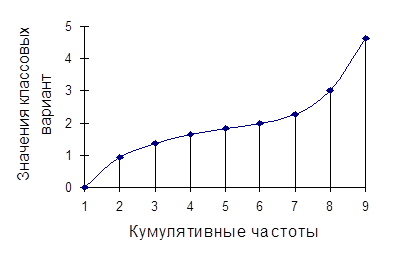 |
Рис. 2.4 Пример графика огивы
Примечание: Неумелое построение графиков приводит к тому, что последние получаются либо в виде островершинных геометрических фигур с узким основанием, либо плосковершинными, чрезвычайно растянутыми по оси абсцисс. В обоих случаях графики оказываются плохо обозримыми, нечетко отображающими закономерность варьирования.
Избежать эти недостатки поможет правило "золотого сечения", согласно которому основание геометрической фигуры должно относиться к ее высоте, как 1:0,62. Применительно к построению вариационной кривой масштабы на осях прямоугольных координат следует выбирать с таким расчетом, чтобы основание кривой было в 1,5-2,0 раза больше ее высоты (т.е. максимальной ординаты). Откладывая по оси абсцисс классы вариационного ряда, следует также доводить крайне из них до нулевых классов, в которых не содержится ни одной варианты. В результате вариационной кривой придается законченный, хорошо обозримый вид.
Date: 2015-09-02; view: 1603; Нарушение авторских прав