
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Подсчет масштабных коэффициентов
|
|
3. Подсчитать по осям ординат для всех трех диаграмм:
 | 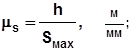 | ||
масштабный коэффициент перемещения
масштабный коэффициент аналога скорости
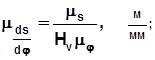 |
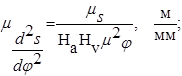 |
масштабный коэффициент аналога ускорения
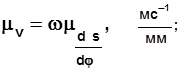 |
масштабный коэффициент скорости
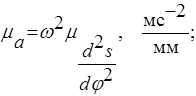 |
масштабный коэффициент ускорения
где h - заданный ход толкателя в м;
smax - наибольшая ордината на графике перемещения
толкателя вмм;
Hа,Hv - полюсные расстояния при первом и втором
графическом интегрировании в мм;
ω - заданная угловая скорость кулачка в с-1.
I.3. Синтез кулачкового механизма с роликовым толкателем
4. Определить основные размеры (радиус начальной шайбы r0, эксцентриситет е) кулачкового механизма с роликовым толкателем из условия обеспечения углов передачи γ12 при подъеме и опускании толкателя больших, чем допустимые заданные углы γпдоп и γопдоп. Для решения неравенства

следует воспользоваться диаграммой S=Ф4(ds/dφ), которую необходимо построить в одинаковых масштабных коэффициентах по обеим осям из диаграмм S=Ф1(φ) и ds/dφ= Ф2(φ), полученных ранее при интегрировании (п.2), исключая параметр φ. При этом необходимо подсчитать либо коэффициент преобразования одной из координат Кv, либо угол наклона отображающей прямой av
Kv=tg bv=ms /mds/dφ=Hvmj; bv=arctg Kv
5. Построить в масштабе теоретический профиль кулачка, применив метод обращения движения. Найти наименьший радиус ρmin выпуклой части теоретического профиля кулачка приближенным геометрическим построением.
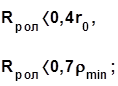 |
6. Принять радиус ролика Rрол толкателя меньшимиз двух условий:
7. Закончить построение плана кулачкового механизма c роликовым толкателем. Вычертить контурной линией практический профиль кулачка, как огибающую параметрического семейства роликов. В одном из положений изобразить роликовый толкатель, показать опоры кулачка и толкателя, кинематическую пару толкателя и ролика. Проставить на плане механизма r0, hmax, ωкул, углы φп, φвв, φоп, φнв, а также обозначить номера всех взаимных положений кулачка и толкателя.
8. Построить график изменения угла давления α12= Ф(φ) для всего рабочего угла поворота кулачка.
I.4. Синтез кулачкового механизма с тарельчатым толкателем
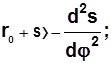 |
9. Определить минимальный радиус кулачка r0 min для механизма с плоским тарельчатым толкателем из условия обеспечения выпуклого профиля кулачка. Для этого можно воспользоваться методом Я.Л. Геронимуса, позволяющим графически решить неравенство
Для решения неравенства необходимо воспользоваться диаграммой S=Ф5(d2s/dφ2), которую необходимо построить в одинаковых масштабных коэффициентах по обоим осям диаграммы. Эта диаграмма строится совмещение двух диаграмм S=Ф1(φ) и d2s/dφ2= Ф3(φ).. При этом необходимо подсчитать либо коэффициент преобразования одной из координат Кa, либо угол наклона отображающей прямой av
Ka=tg ba=ms /md2s/dφ2 =HvHamj2; ba=arctg Ka
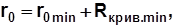 |
10. Подсчитать радиус основной шайбы кулачка
приняв минимальный радиус кривизны профиля кулачка
Rкрив.min.=(10…20) 10-3 м
Если радиус основной шайбы кулачка получается меньше, чем ход толкателя, то следует принять r 0 min=(3…5)h.
11. Построить в масштабе теоретический профиль кулачка, применив метод обращения движения и выделяя кружочками центр тарелки при всех промежуточных положениях толкателя.
12. Построить практический профиль кулачка, проводя перпендикуляры к радиусам (тарелки) через соответствующие точки теоретического профиля. Действительный профиль будет являться огибающей параметрического семейства тарелок.
13. Выбрать радиус тарелки толкателя, учитывая, что величина радиуса тарелки должна быть Rтарелки›│ds/dφ│max. Радиус тарелки Rтар толкателя может быть определен и приближенно после построения практического профиля кулачка по расстоянию от центра тарелки до наиболее удаленной точки касания тарелки с практическим профилем. Радиус тарелки следует принять на (5..8)х10-3м большим, чем найденное расстояние с учетом масштаба построения.
14. Закончить построение плана кулачкового механизма с тарельчатым толкателем. При этом необходимо показать контурной линией практический профиль кулачка, пунктирной линией теоретический профиль, в одном из положений изобразить тарельчатый толкатель с учетом определенного радиуса тарелки Rтар, показать опоры кулачка и толкателя. Проставить на плане механизма r0, hmax, ωкул, углы φп, φвв, φоп, φнв, а также обозначить номера всех взаимных положений кулачка и толкателя.
ЛИСТ 2 ПРОЕКТИРОВАНИЕ ЗУБЧАТОЙ ПЕРЕДАЧИ
Цель листа: Для заданных параметров цилиндрической зубчатой передачи провести геометрический расчет и выполнить чертеж эвельвентной цилиндрической зубчатой передачи внешнего зацепления. Определить также качественные показатели этой передачи
Исходные данные:
Z1, Z2, - числа зубьев колес
m – модуль зубчатой передачи
x1, x2 – коэффициенты смещения инструмента при нарезании зубчатых колес
Параметры исходного контура (ГОСТ 13755-84)
ha*- коэффициент высоты головки зуба
hl*- коэффициент граничной высоты
с* - коэффициент радиального зазора
α- угол профиля исходного контура
2.1. Расчет основных геометрических параметров
1. Делительное межосевое расстояние
а=(z1+z2)m/2
2. Коэффициент суммы смещений
xS=x1+x2
3. Угол зацепления
invaW= inva+2xStga/(z1+z2)
aW=
Величина угла зацепления αw может быть рассчитана итерационным методом, а может быть определена по таблицам инвалют [9, с. 500-503] или [10, с. 422-423]
Величина угла зацепления αw может быть определена по таблицам инвaлют или рассчитана на калькуляторе методом последовательных приближений.
Например inv αw =0,034956, найдем αw.
Напомним, что специальная функция инвалюта угла α равна inv α=tg α – α, где α подставляется в радианах. Например
inv α=tg α – α=inv 20=inv 0,3490658=tg 0,3490658 – 0,3490658=0,01490438
inv 200 =0,014904, inv 300= 0,0537515.
Делим диапазон α попалам и ищем инвалюту 250
inv 250 =0,029975, меньше чем 0,034956, следовательно αw лежит между 250 и 300.
Берем 260, ищем инвалюту
inv 260 =0,0339469, меньше чем 0,034956, следовательно опять αw лежит между 260 и 300. Берем 26,30, ищем инвалюту
inv 26,30 =0,0352092, чуть больше чем 0,034956.
Немного уменьшаем угол при приближении и т.д.
inv 26,250 = 0,0349965
inv 26,2450 = 0,034975
inv 26,2430 = 0,0349667
inv 26,24250 =0,03496467
inv 26,2420 = 0,034962
inv 26,24140 =0,03496 Точность достаточная.
4. Межосевое расстояние
aw=(z1+z2) m cosa /(2cosaw)
Величину отношения косинусов угла профиля инструмента α и угла зацепления передачи αw можно не подсчитывать, а взять из таблицы [9, с. 500-503].
5. Делительный диаметр шестерни и колеса
d1=z1m
d2=z2m
6. Передаточное число
u=z2/z1
7. Начальный диаметр шестерни и колеса
dw1=2aw/(u+1)
dw2=2aw u/(u+1)
8. Коэффициент воспринимаемого смещения
y=(aw- a)/m
9. Коэффициент уравнительного смещения
Dy= xS - y
10.Диаметр вершин зубьев шестерни и колеса
da1=d1+2(ha*+ x1-Dy)m
da2=d2+2(ha*+ x2-Dy)m
11. Диаметр впадин шестерни и колеса
df1=d1-2(ha*+ c*- x1)m
df2=d2-2(ha*+ c*- x2)m
Проверка расчетов, выполненных по пунктам 1-11
12. Межосевое расстояние
aw=rw1+rw2
aw=r1+r2 +ym
aw=ra1+rf2 +c*m
aw=rf1+ra2 +c*m
2.2 Расчет вспомогательные геометрических параметров
13. Основной диаметр шестерни и колеса
db1=d1cosa
db2=d2cosa
14. Угловой шаг зубьев шестерни и колеса
t1=3600/z1
t2=3600/z2
15. Хорда делительной окружности, соответствующая угловому шагу зубьев шестерня и колеса
Р1=d1sin(t1/2)
Р2=d2sin(t2/2)
16. Окружная толщина зуба по делительной окружности шестерни и колеса
S1=(p/2+2 x1 tga)m
S2=(p/2+2 x2 tga)m
17. Высота зуба
h=(da1-df1)/2
h=(da2-df2)/2
h=(2ha*+c*-Dy)m
18. Угол профиля зуба в точка на окружности вершин шестерни αа1 и колеса αа2.
сosaa1=db1/da1 aa1=
сosaa2=db2/d aa2=
19. Радиус кривизны активного профиля зуба в нижней точке шестерни и колеса
rp1=awsinaw – rb2tgaa2
rp2=awsinaw – rb1tgaa1
20. Угол развернутости активного профиля зуба в нижней точке шестерни и колеса
nр1=2rp1/db1
nр2=2rp2/db2
21. Шаг зацепления
Pa=pmcosa
Date: 2015-09-02; view: 527; Нарушение авторских прав