Определение ранга матрицы. Линейная зависимость строк матрицы означает, что хотя бы одна строка матрицы является линейной комбинацией остальных

Линейная зависимость строк матрицы означает, что хотя бы одна строка матрицы является линейной комбинацией остальных.

Пример.

Определить каково число линейно независимых строк (столбцов) матрицы А.

Умножим первую строку на -2 сложим со 2 – ой строкой

Умножим первую строку на -3 сложим с 3 –ей строкой

Умножим 2 строку на -1 сложим с 3 –ей строкой

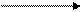
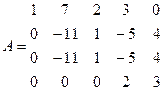
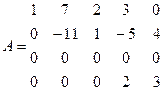
Отбросим нулевую строку

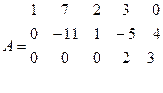
Поменяем столбцы местами, получим ступенчатую матрицу, у которой существует минор 3 – го порядка (три ненулевых элемента на главной диагонали)

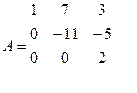= -2 ≠ 0, значит ранг матрицы =3 и исходная матрица имеет 3 линейно независимых строки (столбца).

Теорема о ранге матрицы

Ранг матрицы = максимальному числу линейно независимых строк (столбцов).

Пример

Найти ранг матрицы (число линейно независимых строк (столбцов)).

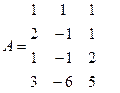
Матрица имеет размер 4 x 3, значит r (A) ≤ 3.

Приведем матрицу к ступенчатому виду, с помощью элементарных преобразований.

1) Транспонируем матрицу A.

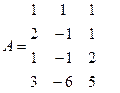
Умножим 1 – ую строку на -1, сложим ее со 2 и 3 –ей строками.

-1

-1

Поменяем местами 2 и 3 строки.

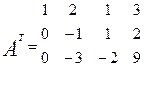
Умножим 2 строку на 3 и сложим с элементами 3 строки.

 

 

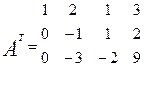
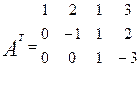
Получим ступенчатую матрицу, размером 3 x 4, у которой 3 ненулевых элемента на главной диагонали, значит r (A) = 3 9 (Число линейно независимых строк тоже = 3).

Минор 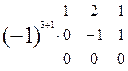= 3 ≠ 0

 

Date: 2015-09-02; view: 483; Нарушение авторских прав