
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Приложения определенного интеграла в геометрии
|
|
Неопределенный интеграл
Таблица интегралов
1.  ; 2.
; 2. 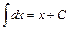 ;
;
3.  ; 4.
; 4.  ;
;
5.  ; 6.
; 6. 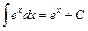 ;
;
7. 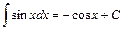 ; 8.
; 8.  ;
;
9. 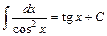 ; 10.
; 10. 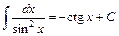 ;
;
11. 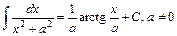 ; 12.
; 12.  ;
;
13.  ; 14.
; 14. 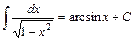 ;
;
15.  ; 16.
; 16.  ;
;
17. 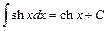 ; 18.
; 18.  .
.
Основные свойства неопределенного интеграла
19. 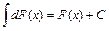 ; 20.
; 20.  ;
;
21.  ; 22.
; 22.  ;
;
23. Если  , то
, то 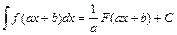 .
.
Определенный интеграл
1.  – формула Ньютона-Лейбница.
– формула Ньютона-Лейбница.
2.  – формула интегрирования по частям.
– формула интегрирования по частям.
3. Геометрический смысл определенного интеграла: интеграл 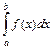 численно равен площади криволинейной трапеции, ограниченной слева и справа прямыми
численно равен площади криволинейной трапеции, ограниченной слева и справа прямыми 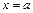 и
и 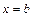 , осью
, осью 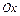 и сверху графиком функции
и сверху графиком функции  (рис. 1).
(рис. 1).
 | |||
 | |||
Рис. 1 Рис. 2
Приложения определенного интеграла в геометрии
4. Площадь криволинейной трапеции в декартовой прямоугольной системе координат (рис. 1) вычисляется по формуле:  . Если
. Если  на
на 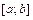 (график функции лежит ниже оси
(график функции лежит ниже оси 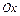 ), то
), то 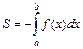 .
.
5. Если криволинейная трапеция ограничена сверху кривой, заданной параметрически  то площадь фигуры равна:
то площадь фигуры равна:  , где
, где  и
и  соответствуют значениям
соответствуют значениям 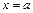 и
и 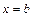 .
.
6. Площадь криволинейного сектора, ограниченного кривой 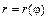 и двумя лучами
и двумя лучами 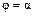 и
и  в полярных координатах (рис. 2) вычисляется по формуле:
в полярных координатах (рис. 2) вычисляется по формуле:  .
.
7. Если кривая задана уравнением  в декартовой прямоугольной системе координат, то длина этой кривой от точки
в декартовой прямоугольной системе координат, то длина этой кривой от точки 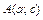 до точки
до точки  вычисляется по формуле:
вычисляется по формуле: 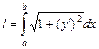 . Если кривая
. Если кривая 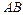 определяется уравнением
определяется уравнением  , то
, то  .
.
8. Если кривая задана параметрически  , то длина кривой
, то длина кривой 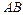 вычисляется по формуле:
вычисляется по формуле: 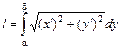 , где
, где  и
и  соответствуют значениям
соответствуют значениям 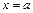 и
и 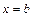 .
.
9. Если кривая задана уравнением 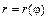 в полярных координатах, то ее длина между лучами
в полярных координатах, то ее длина между лучами 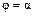 и
и  равна:
равна: 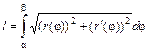 .
.
10. Объем тела, образованного вращением вокруг оси 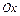 криволинейной трапеции (рис. 1), вычисляется по формуле:
криволинейной трапеции (рис. 1), вычисляется по формуле:  . Если эту криволинейную трапецию вращать вокруг оси
. Если эту криволинейную трапецию вращать вокруг оси  , то объем тела вращения равен
, то объем тела вращения равен  , причем
, причем 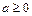 .
.
 11. Если криволинейная трапеция ограничена кривой
11. Если криволинейная трапеция ограничена кривой  (
( ), осью
), осью  и прямыми
и прямыми 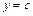 и
и  (рис. 3), то объем полученного тела вращения вокруг оси
(рис. 3), то объем полученного тела вращения вокруг оси  равен:
равен:  .
.
Рис. 3
12. Если дуга кривой, заданная в декартовых прямоугольных координатах 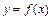 , где
, где 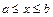 , вращается вокруг оси
, вращается вокруг оси 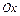 , то площадь поверхности вращения вычисляется по формуле:
, то площадь поверхности вращения вычисляется по формуле: 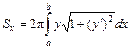 .
.
13. Если дуга кривой  , где
, где 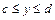 вращается вокруг оси
вращается вокруг оси  , то площадь поверхности вращения вычисляется по формуле:
, то площадь поверхности вращения вычисляется по формуле: 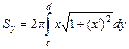 .
.
14. Если дуга кривой задана параметрически 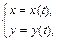 где
где  , то площадь поверхности вращения вокруг оси
, то площадь поверхности вращения вокруг оси 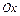 равна:
равна:  .
.
15. Если дуга задана в полярных координатах 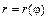 , где
, где  , то
, то  .
.
Date: 2015-09-02; view: 387; Нарушение авторских прав