Основные элементы окна

Кнопка РАСЧЕТ — вычисление параметра , при котором возможно преобразование;

Кнопка ПОСТРОИТЬ ГРАФИК ФУНКЦИИ — график поляризационной характеристики при заданных параметрах;

Поле Начальный угол поляризации — значение ;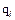

Поле Начальный сдвиг фаз между TE и TM — значение ;

Поле Наведенный сдвиг фаз после первой ячейки — значение ;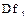

Поле Наведенный сдвиг фаз после третьей ячейки — значение ;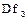

Поле Угол поляризации на выходе — значение ;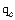

Поле Значение сдвига фаз на выходе — значение .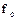

В поля группы «Границы интервала» вводятся значения левого и правого концов интервала смены знака поляризационной функции.

Переключатель «Тип вращателя» позволяет выбрать режимы линейного и произвольного вращения.

Список «Тип преобразования» позволяет выбрать одну из следующих схем преобразования: TE®TM, TM®TE, ПКП®TE, ЛКП®TE, ПКП®TM, ЛКП®TM, ПКП®ЛКП, ЛКП®ПКП, TE®ПКП, TE®ЛКП, TM®ПКП, TM®ЛКП.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Эффект Керра.

2. Эффект Поккельса.

3. Тензор показателей преломления.

4. Устройство и принцип работы фазового модулятора емкостного типа.

5. Устройство и принцип работы фазового модулятора бегущей волны.

6. Виды поляризации электромагнитных волн.

7. Устройство и принцип работы TEÛTM-преобразователя.

8. Устройство и принцип работы интегрально-оптического преобразователя поляризации.

ЛИТЕРАТУРА

1. Интегральная оптика / Под ред. Тамира Т. — М.: Мир, 1978.

2. Клэр Ж.-Ж. Введение в интегральную оптику. — М.: Сов. Радио, 1980.

3. Свечников Г.С. Интегральная оптика. — Киев: Наукова думка, 1988.

4. Хансперджер Р. Интегральная оптика. Теория и технология. — М.: Мир, 1985.

ЛАБОРАТОРНАЯ РАБОТА №5

Электродинамический анализ собственных волн
оптических волноводов

ЦЕЛЬ РАБОТЫ: получение навыков расчёта дисперсионных характеристик плоских трёхслойных оптических волноводов при помощи программы MathCad.

ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

1. Плоский трехслойный волновод с постоянной величиной
показателя преломления световедущей пленки

В предлагаемой лабораторной работе производится электродинамический анализ плоского трехслойного диэлектрического оптического волновода (световод показан на рисунке 1).

Рисунок 1

Рассматриваемая структура состоит из трех диэлектрических слоев: волноведущей пленки с показателем преломления 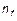, покровного слоя (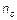) и подложки ().

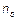Рассмотрим электродинамическую теорию плоского трехслойного оптического волновода, базирующуюся на использовании уравнений Максвелла.

Обозначим через 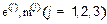относительные диэлектрические и магнитные проницаемости подложки, световедущей пленки и покровного слоя, соответственно. Будем решать задачу при следующих допущениях:

1. Показатель преломления световедущей пленки 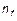является постоянным и не зависит от поперечной координаты .

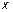2. Будем считать, что волноведущая структура является неограниченной вдоль оси .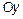

3. Будем считать, что составляющие векторов электромагнитного поля в покровном слое и подложке экспоненциально уменьшаются по закону 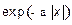, где 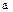— положительный коэффициент.

В плоском трехслойном оптическом волноводе возможно распространение двух типов собственных волн (волноводных мод):

— TE (поперечно-электрические волны), у которых присутствует продольная составляющая вектора напряженности магнитного поля 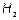, а также компоненты 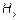и ;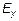

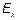— TM (поперечно-магнитные волны), у которых присутствует продольная составляющая вектора напряженности электрического поля , а также компоненты и .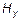

Как будет показано ниже, анализ для TE и TM-мод может производиться раздельно друг от друга.

Будем представлять комплексные амплитуды напряженностей электрического и магнитного полей распространяющихся волн в следующем виде:

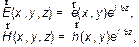(1)

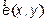где и 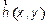— функции, определяющие электрическое и магнитное поля в поперечной плоскости волновода; 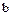— постоянная распространения какой-либо волноводной моды.

Запишем уравнения Максвелла для электромагнитного поля в произвольном диэлектрическом слое волновода:

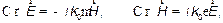(2)

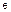где и 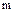— относительные диэлектрическая и магнитная проницаемости слоя; 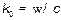— волновое число для вакуума.

Записывая (2) в проекциях на оси декартовой системы координат, с учетом принятых допущений получаем две системы уравнений:

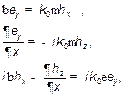(3)

которая описывает электромагнитное поле TE-мод и

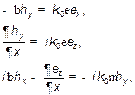(4)

которая описывает электромагнитное поле TM-мод.

1. Дисперсионное уравнение для TE-мод
плоского трехслойного волновода

Рассмотрим сначала систему уравнений (3), которая описывает электромагнитное поле TE-моды. Выражая из первых двух уравнений системы (3) составляющи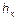е и , и подставляя эти выражения в третье уравнение из (3), получаем однородное уравнение Гельмгольца для составляющей :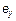

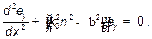(5)

где 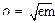— показатель преломления слоя.

Тангенциальная составляющая определяется из следующего соотношения:

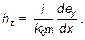(6)

Получим дисперсионное уравнение для TE-мод. Запишем решение уравнения Гельмгольца (5) для подложки, световедущей пленки и покровного слоя волновода, показанного на рис. 1.

В области 1 (подложка) решение уравнения (5) является экспоненциально затухающим:

(7)

где , 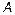— неизвестная постоянная.

Составляющая 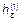определяется из уравнения (6):

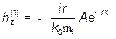(8)

В области 2 (световедущая пленка) решение уравнения (5) представляет собой распространяющуюся волну:

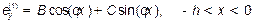(9)

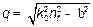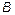где , и 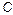— неизвестные постоянные.

Составляющая 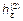определяется из уравнения (6):

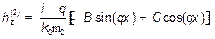(10)

В области 3 (покровный слой) решение уравнения (5) является экспоненциально затухающим:

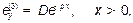(11)

где 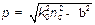, — неизвестная постоянная.

Составляющая 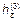определяется из уравнения (6):

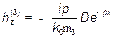(12)

Воспользуемся граничными условиями, заключающимися в непрерывности тангенциальных составляющих векторов напряжённости электрического и магнитного полей на границе раздела двух диэлектрических сред:

(13)

Подставляя в граничные условия (13) явные выражения для составляющих (7)-(12), приходим к системе алгебраических уравнений относительно неизвестных коэффициентов:

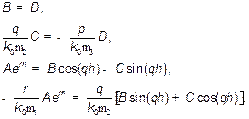(14)

Равенство нулю определителя системы уравнений (14) соответствует дисперсионному уравнению для TE-мод плоского трёхслойного оптического волновода:

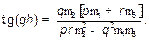(15)

На практике слои волноводы изготовляются из немагнитных диэлектриков, у которых 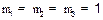. В этом случае дисперсионное уравнение (15) упрощается:

(16)

Уравнение (16) выражает связь 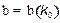. Однако явным образом из него эту зависимость получить нельзя и дисперсионное уравнение (16) может быть решено только численно. Различные корни решения соответствуют разным TE-модам.

2. Дисперсионное уравнение для TM-мод плоского
трехслойного волновода

Дисперсионное уравнение для TM-мод получается аналогичным образом с использованием системы уравнений (4).

Однако его можно записать автоматически, исходя из уравнения (15) для TE-мод. Для этого воспользуемся принципом перестановочной двойственности и в уравнении (15) произведем замену:

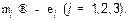
Дисперсионное уравнение для TM-мод имеет следующий вид:

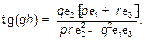(17)

3. Дисперсионное уравнение для TE и TM-мод плоского трехслойного
волновода в нормированном виде

Дисперсионная характеристика представляет собой график зависимости 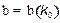. Однако, как видно из уравнений (16) и (17) данную зависимость в явном виде получить не представляется возможным. Поэтому дисперсионное уравнение для собственных волн регулярной линии передачи можно записать следующим образом:

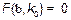, (18)

которое в общем случае является трансцендентным и может быть решено только численными методами.

На первом этапе производится переход от величин 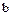и 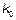, имеющих размерность 1/м к безразмерным параметрам. Будем использовать два нормированных параметра:

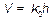— нормированная ширина волновода;

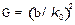— нормированная постоянная распространения.

Используя новые нормированные параметры, несложно переписать уравнение (16) для TE-мод в следующем виде:

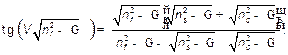(19)

В нормированных переменных дисперсионное уравнение имеет вид:

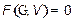. (20)

Уравнение для частот отсечек для TE-мод несложно получить из (19) при :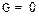

(21)

Путем численного решения уравнения (21) определяются его корни 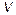, соответствующие частотам отсечек TE-мод. Первый корень является нормированной частотой отсечки нулевой TE-моды, второй корень — первой TE-моды и т.д.

Аналогично несложно записать дисперсионное уравнение для TM-мод (17) в нормированном виде:

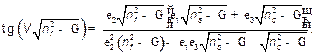(22)

Нормированные частоты отсечек TM-мод определяются из следующего соотношения, которое получается из (22) при :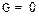

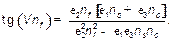(23)

Date: 2015-09-02; view: 431; Нарушение авторских прав