Определитель 2-го и 3-го порядков

Понятие определителя связано с понятием квадратной матрицы. Определитель квадратной матрицы – это число, поставленное в соответствие данной матрице:

Обозначается: = d= D = det A =|A|=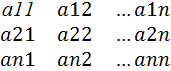

A₂= 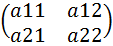_.,det A₂= 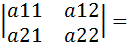a₁₁*a₂₂-a₂₁*a₁₂

A₂ = 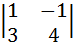=4+3=7 Правило Сарруса

A₃= 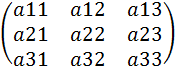, det A₃= ₌ , где a₁₁, а₂₂, а₂₃ – главная диагональ

а₃₁, а₂₂, а₁₃ – побочная диагональ

A₃= 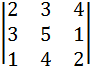= 2*5*2+3*4*4+3*1*1-1*4*2-3*3*2=25

Теорема Лапласа (точнее частный случай Т.Л.)

Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения:

= a_i1А_i1 + a_i2 A_i2+…+ a_inA_in= 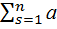_is A_is– разложение по элементам i-й строки;

= a_1jА_1j + a_2j A_2j+…+ a_njA_nj= 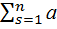_sjA_sj– разложение по элементам j-ого столбца;

Пример: вычислить определитель матрицы А

А= 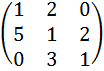, используя разложение по элементам а) первой

строки; б) второго столбца.

а) Найдём алгебраические дополнения элементов первой строки:

А₁₁=(-1)¹⁺¹ 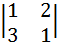= 1-6=-5

А₁₂=(-1)¹⁺² = -(5-0) = -5

А₁₃=(-1)¹⁺³ = 15-0=15

по т. Лапласа: = a₁₁A₁₁+ a₁₂ A₁₂+ a₁₃ A₁₃ = 1(-5)+2(-5)+0+15=-15

б) Найдём алгебраические дополнения элементов второго столбца:

А₁₂=(-1)²⁺¹ = (-1)³5=-5

А₂₂=(-1)²⁺² = 1

А₃₂=(-1)³⁺² 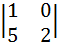= -1-2=-2

по т. Лапласа: = a₁₂A₁₂+ a₂₂ A₂₂+ a₃₂ A₃₂ =

=2(-5)+1*1+3*(-2)= -10+1-6=-15 Ответ: -15.

Д/3 Найти определитель разложением его по элементам первой строки

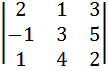= = 2*(-1)¹⁺¹ +1*(-1)¹⁺² 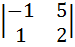+3*(-1)¹⁺³ =

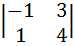= 2(6-20)-(-2-5)+3(-4-3)=2*(-12)+7-21=-28-14=-42

Ответ:-42

Пример. Вычислить определитель.

Det A=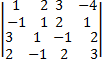

Решение. Приведём определитель к виду, в котором в первой строке будут числа 1,0,0,0. Для этого первый столбец будем прибавлять к последующим столбцам, умножая его на числа (-2); (-3); (+4)

detA= 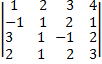= = воспользуемся разложением полученного определителя по элементам первой строки:

a₁₁A₁₁+0+0+0=1*(-1)¹⁺¹M₁₁=1*(-1)¹⁺¹ 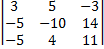=3*(-10)*11+ (-5)*(-4)*(-3)+5*14*(-5)-(-5)*(-10)*(-3)-3*(-4)*14-(-5)*5*11=-330-60-350+150+168+273=-149

Ответ: -149

Обратная матрица.

Обращение матриц второго и третьего порядка.

Квадратная матрица А^-1 называется обратной по отношению к матрице А, если её умножение как справа, так и слева на данную матрицу приводит к единичной матрице.

А^-1*А=А*А^-1=E.

Только квадратная матрица имеет обратную и тоже квадратную, однако не каждая квадратная матрица имеет обратную, а только та, ≠0 у которой определитель ≠0 называется она невырожденной или неособенной. В случае если =0, то матрица вырожденная или особенная.

Теорема. Любая неособенная матрица имеет единственную обратную ей матрицу, нахождение обратной матрицы называется Обращения данной матрицы.

Для обращения матрицы можно воспользоваться формулой:

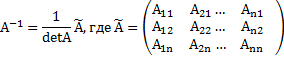
Матрица называется союзной по окончанию к матрице А.

Алгоритм вычисления обратной матрицы:

1) Найти определитель данной (исходной) матрицы (если ≠0 то матрица А – невырожденная и обратная матрица существует).

2) Находим алгебраические дополнения элементов матрицы А.

3) Составляем союзную и обратную матрицы.

4) Проверяем правильность вычисления обратной матрицы A^-1, исходя из определения A^-1*A=A*A^-1=E

Пример. Обратить матрицу первого порядка.

Решение.

1) Вычисляем определитель данной матрицы: =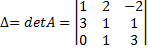

= 1*1*3+3*1*(-2)+0*2*1-0*1*(-2)-1*1*1-3*2*3=3-6+0-0-1-18=-22

2) Находим алгебраические дополнения элементов матрицы А.

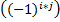
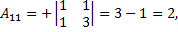
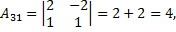
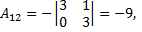
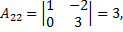
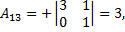
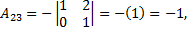
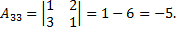
3) Составляем союзную и обратную матрицы:

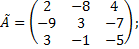
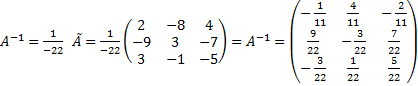
4) Проверка.

=

=

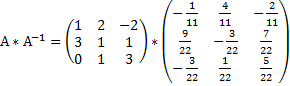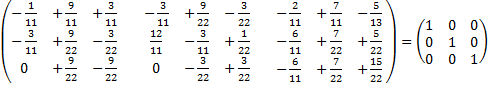
И А^-1*А=Е аналогично.

Задание 1.

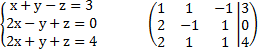
Представим систему в виде матричного уравнение A*x=В, тогда

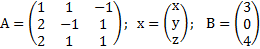
Решением такого уравнения является вектор-столбец

X=A^-1*B, если detA≠0

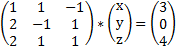
Обратим матрицу А: detA=1*(-1)*1+1*1*2+2*1*(-1)-(-1)*(-1)*2-1*2*1-1*1*1=-1+2-2-2-2-1=-6

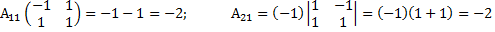
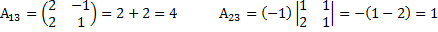
x=3-y+z

6-2y+2z-y+z=0

6-3y+3z=0

Z=y-2

3-y+y-2

2x+y+y-2=4

2(3-y+y-2)+2y-2=4

2+2y-2=4

2y=4

Y=2

Z=0

X=3-2+0=1

1+2-0=3-ϐ

2-2+0=0- ϐ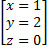

2+2+0=4- ϐ

Date: 2015-09-02; view: 354; Нарушение авторских прав