К выполнению раздела III

Выборочное наблюдение - это один из видов не сплошного наблюдения, при котором учету подлежит только часть единиц наблюдаемого явления, и отбор единиц в выборочную совокупность производится по определенному закону. Статистические характеристики, полученные на основе выборочного наблюдения - выборочная средняя, выборочная дисперсия и т.д. всегда отличаются по величине от статистических характеристик генеральной совокупности, охватывающей все единицы изучаемого явления.

Разница статистических характеристик генеральной и выборочной совокупности называется ошибкой выборки или репрезентативности и обозначается

где х_{ср.генер}. и х_{ср.выбор.} - соответственно генеральная и выборочная средние.

Применяя выборочный метод наблюдения, необходимо рассчитать ошибки выборки (ошибки репрезентативности), т.к. генеральные и выборочные харак- теристики, как правило, не совпадают, а отклоняются на некоторую величину ε.

Принято вычислять два вида ошибок выборки - среднюю 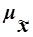и предельную .

Для расчета средней ошибки выборки 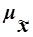применяются различные формулы в зависимости от вида и способа отбора единиц из генеральной совокупности в выборочную.

Для собственно-случайной и механической выборки с бесповторным способом отбора средняя ошибка 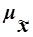для выборочной средней 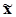определяется по формуле

,

где – общая дисперсия изучаемого признака,

N – число единиц в генеральной совокупности,

n – число единиц в выборочной совокупности.

Предельная ошибка выборки определяет границы, в пределах которых будет находиться генеральная средняя:

,

,

где – выборочная средняя,

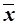– генеральная средняя.

Предельная ошибка выборки кратна средней ошибке 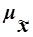с коэффициентом кратности t ( называемым также коэффициентом доверия):

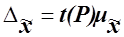
Коэффициент кратности t зависит от значения доверительной вероятности Р, гарантирующей вхождение генеральной средней в интервал 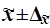, называемый доверительным интервалом.

Наиболее часто используемые доверительные вероятности Р и соответствующие им значения t задаются следующим образом (табл. 15):

Таблица 15

По условию выборочная совокупность насчитывает 25 предприятий, выборка 20% собственно случайная, следовательно, генеральная совокупность включает 500 предприятий. Выборочная средняя , дисперсия определены раннее в разделе 2. Значения параметров, необходимых для решения задачи, представить в табл. 16:

Таблица 16

Р	t	n	N
0,954

Рассчитаем среднюю ошибку выборки:

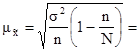
Рассчитаем предельную ошибку выборки:

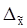
Определим доверительный интервал для генеральной средней:

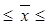
Вывод.

2. Определение ошибки выборки для доли фирм со среднесписочной численностью менеджеров 35 человек и более, а также границ, в которых будет находиться генеральная доля

Доля единиц выборочной совокупности, обладающих тем или иным заданным свойством, выражается формулой

,

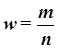где m – число единиц совокупности, обладающих заданным свойством;

n – общее число единиц в совокупности.

Для собственно-случайнойвыборки с бесповторным способом отбора предельная ошибка выборки 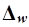доли единиц, обладающих заданным свойством, рассчитывается по формуле

,

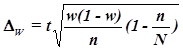где w – доля единиц совокупности, обладающих заданным свойством;

(1-w) – доля единиц совокупности, не обладающих заданным свойством,

N – число единиц в генеральной совокупности,

n – число единиц в выборочной совокупности.

Предельная ошибка выборки 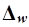определяет границы, в пределах которых будет находиться генеральная доля р единиц, обладающих исследуемым признаком:

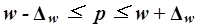
По условию Задания 3 исследуемым свойством фирм является равенство или превышение среднесписочной численности менеджеров величины 35 человек.

Число фирм с данным свойством определяется из табл. 1и 5:

m=

Рассчитаем выборочную долю:

Рассчитаем предельную ошибку выборки для доли:

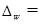
Определим доверительный интервал генеральной доли:

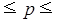
Вывод.

Date: 2015-09-02; view: 252; Нарушение авторских прав