
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Задание 2. Целью выполнения данного задания является выявление наличия корреляционной связи между факторным и результативным признаками
|
|
Целью выполнения данного задания является выявление наличия корреляционной связи между факторным и результативным признаками, а также установление направления связи и оценка ее тесноты.
По условию задания 2 факторным является признак Среднесписочная численность менеджеров, результативным – признак Объем продаж.
Установление наличия и характера корреляционной связи между признаками Среднесписочная численность менеджеров и Объём продаж методами аналитической группировки и корреляционных таблиц
1а. Применение метода аналитической группировки
Аналитическая группировка строится по факторному признаку Х и для каждой j-ой группы ряда определяется среднегрупповое значение 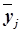 результативного признака Y. Если с ростом значений фактора Х от группы к группе средние значения
результативного признака Y. Если с ростом значений фактора Х от группы к группе средние значения 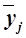 систематически возрастают (или убывают), между признаками X и Y имеет место корреляционная связь. Сделать вывод по данным таблицы 6.
систематически возрастают (или убывают), между признаками X и Y имеет место корреляционная связь. Сделать вывод по данным таблицы 6.
1б. Применение метода корреляционных таблиц
Корреляционная таблица строится как комбинация двух рядов распределения по факторному признаку Х и результативному признаку Y. На пересечении j -ой строки и k -ой графы таблицы указывается число единиц совокупности, входящих в j -ый интервал по признаку X и в k -ый интервал по признаку Y. Концентрация частот около диагонали построенной таблицы свидетельствует о наличии корреляционной связи между признаками - прямой или обратной. Связь прямая, если частоты располагаются по диагонали, идущей от левого верхнего угла к правому нижнему, обратная - по диагонали от правого верхнего угла к левому нижнему.
Для построения корреляционной таблицы необходимо знать величины и границы интервалов по двум признакам X и Y. Для факторного признака Х – Среднесписочная численность менеджеров эти величины известны из табл. 7
Определим величину интервала для результативного признака Y – Объем продаж при k = 6.
Границы интервалов ряда распределения результативного признака Y имеют вид:
Таблица 10
| Номер группы | Нижняя граница, млн руб. | Верхняя граница, млн руб. |
Подсчитывая для каждой группы число входящих в нее предприятий, получаем интервальный ряд распределения результативного признака (табл. 11).
Таблица 11
Интервальный ряд распределения фирм по объёму продаж
| Группы предприятий по объёму продаж, млн руб., у | Число предприятий, fj |
| ИТОГО |
Используя группировки по факторному и результативному признакам, строим корреляционную таблицу (табл. 12).
Таблица 12
Корреляционная таблица зависимости объема продаж
от среднесписочной численности менеджеров
| Группы предприятий по среднесписочной численности менеджеров, чел. | Группы предприятий по объёму продаж, млн руб. | ИТОГО | |||||
| ИТОГО |
2. Измерение тесноты корреляционной связи с использованием коэффициента детерминации 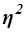 и эмпирического корреляционного отношения
и эмпирического корреляционного отношения 
Коэффициент детерминации 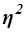 характеризует силу влияния факторного (группировочного) признака Х на результативный признак Y и рассчитывается как доля межгрупповой дисперсии
характеризует силу влияния факторного (группировочного) признака Х на результативный признак Y и рассчитывается как доля межгрупповой дисперсии 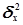 признака Y в его общей дисперсии
признака Y в его общей дисперсии 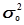 :
:
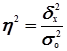
где  – общая дисперсия признака Y,
– общая дисперсия признака Y,
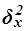 – межгрупповая (факторная) дисперсия признака Y.
– межгрупповая (факторная) дисперсия признака Y.
Общая дисперсия  характеризует вариацию результативного признака, сложившуюся под влиянием всех действующих на Y факторов (систематических и случайных) и вычисляется по формуле
характеризует вариацию результативного признака, сложившуюся под влиянием всех действующих на Y факторов (систематических и случайных) и вычисляется по формуле
 , (1)
, (1)
где yi – индивидуальные значения результативного признака;
 – общая средняя значений результативного признака;
– общая средняя значений результативного признака;
n – число единиц совокупности.
Межгрупповая дисперсия 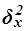 измеряет систематическую вариацию результативного признака, обусловленную влиянием признака-фактора Х (по которому произведена группировка) и вычисляется по формуле
измеряет систематическую вариацию результативного признака, обусловленную влиянием признака-фактора Х (по которому произведена группировка) и вычисляется по формуле
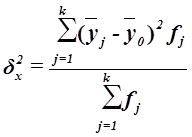 , (2)
, (2)
где 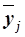 –групповые средние,
–групповые средние,
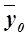 – общая средняя,
– общая средняя,
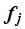 –число единиц в j-ой группе,
–число единиц в j-ой группе,
k – число групп.
Для расчета показателей  и
и 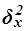 необходимо знать величину общей средней
необходимо знать величину общей средней 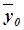 , которая вычисляется как средняя арифметическая простая по всем единицам совокупности:
, которая вычисляется как средняя арифметическая простая по всем единицам совокупности:

Значения числителя и знаменателя формулы имеются в табл.6 (графы 3 и 4 итоговой строки). Используя эти данные, получаем общую среднюю  :
:
Для расчета общей дисперсии  применяется вспомогательная таблица 13.
применяется вспомогательная таблица 13.
Таблица 13
Вспомогательная таблица для расчета общей дисперсии
| Номер предприятия | Объём продаж, млн. руб. | 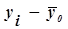
| 
|
| Итого |
Рассчитаем общую дисперсию:
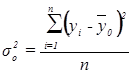 =
=
Для расчета межгрупповой дисперсии 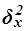 строится вспомогательная таблица 14. При этом используются групповые средние значения
строится вспомогательная таблица 14. При этом используются групповые средние значения 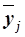 из табл. 6 (графа 5).
из табл. 6 (графа 5).
Таблица 14
Вспомогательная таблица для расчета межгрупповой дисперсии
| Группы предприятий по среднесписочной численности менеджеров, чел., x | Число предприятий, fj | Среднее значение в группе, млн руб.

| 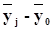
| 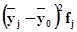
|
| ИТОГО |
Рассчитаем межгрупповую дисперсию:

Определяем коэффициент детерминации:

Эмпирическое корреляционное отношение  оценивает тесноту связи между факторным и результативным признаками и вычисляется по формуле
оценивает тесноту связи между факторным и результативным признаками и вычисляется по формуле

Рассчитаем показатель  :
:
Date: 2015-09-02; view: 394; Нарушение авторских прав