Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Третья теорема разложения
|
|
Если изображением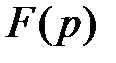 
искомой функции 
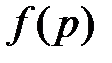служит функция комплексного аргумента, регулярная справа от прямой 
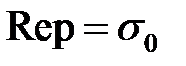, а на этой прямой и слева от нее не имеющая других особенностей, кроме конечного множества полюсов и существенно особых точек, то оригиналом для этой функции случит функция 
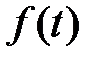, определяемая по формуле:
.
Пример 3.
Найти оригинал для
, 
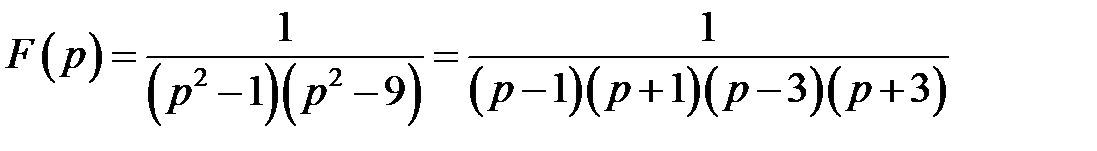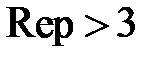
Решение:
, 
, 
, 
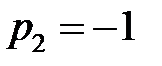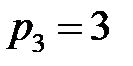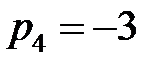- полюсы I порядка.
| -3 |
| -1 |
|
|
|
|
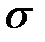
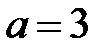
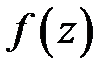в ее особых точках. Если точка 
является простым плюсом (полюсом первого порядка), то для вычисления вычета имеет место формула:
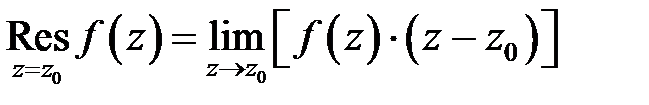
Если точка является полюсом 
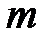-го порядка функции 
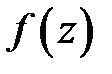, то
≓ 
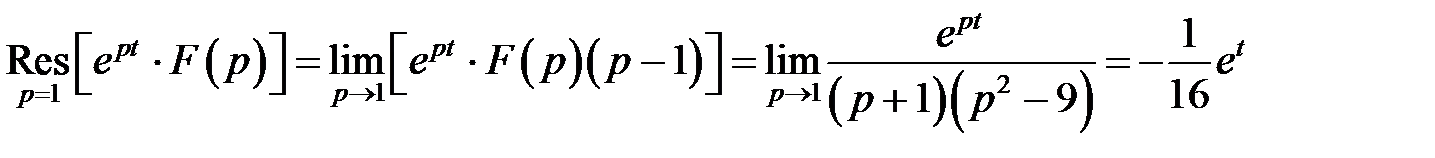
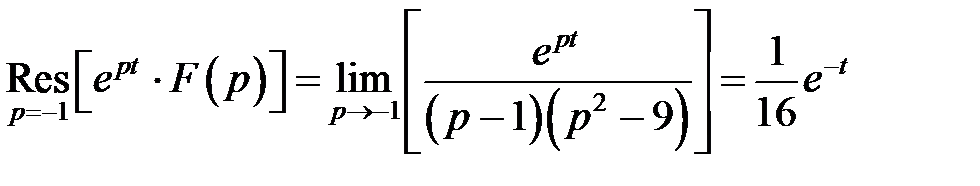
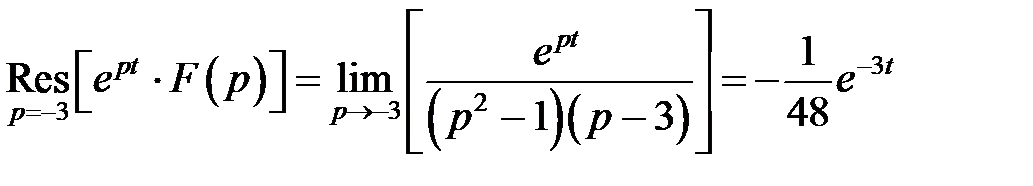
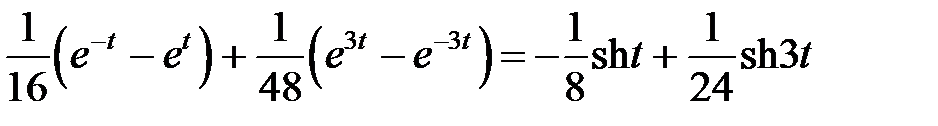
(результаты совпадают с предыдущими)
Пример 4.
Найти оригинал для:
Решение:
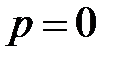- полюс I порядка
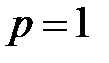- полюс II порядка
≓ 
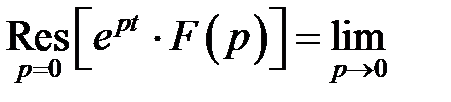
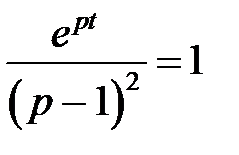
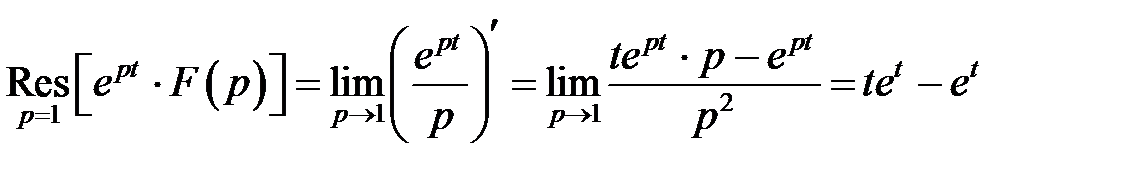
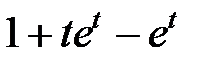
Date: 2015-09-02; view: 2004; Нарушение авторских прав