Запись и решение СЛАУ с помощью матриц

Матрицы позволяют вести очень компактную запись систем линейных алгебраических уравнений (СЛАУ). Обратимся к СЛАУ, представленной в алгебраической форме:

b₁₁v₁ + b₁₂v₂ + … +b_1nv_n + w₁ = 0

b₂₁v₁ + b₂₂v₂ + … +b_2nv_n + w₂ = 0

… … … ….(M.23)

… … … …

b_r1v₁ + b_r2v₂ + … +b_rnv_n + w_r = 0

Введём прямоугольную матрицу коэффициентов этих уравнений

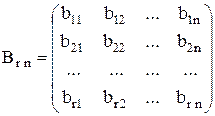, (M.24)

матрицу-столбец (вектор-столбец) неизвестных

, (M.25)

вектор-столбец свободных членов

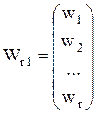(M.26)

и нулевой вектор-столбец правой части системы (M.23)

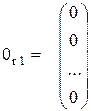. (M.27)

В соответствие с операциями над матрицами, изложенными в предыдущем разделе, мы можем записать матричный эквивалент системы (M.23) кратко

B_{r n} * V_{n 1} + W_{r 1} = 0_{r 1} (M.28)

или развёрнуто

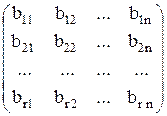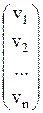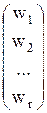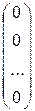* + = . (M.29)

Когда в СЛАУ число уравнений равно числу неизвестных, то матрица коэффициентов становится квадратной. Если определитель такой матрицы не равен нулю, то матрица её коэффициентов будет неособенной. В таком случае существует обратная к ней матрица, с помощью которой просто записывается решение системы.

Пусть СЛАУ

A_{n n} * X_{n 1} = b_{n 1}. (M.30)

характеризуется неособенной матрицей коэффициентов (detA ≠ 0), а ранг расширенной матрицы (A_nnb_n1) равен рангу матрицы коэффициентов, т.е. rank(A) = rank(Ab). Такая система называется совместной.

Умножив систему (M.30) слева на обратную матрицу A_nn^-1, мы получим решение данной СЛАУ в виде вектора неизвестных:

X_{n 1} = A_nn^-1*b_{n 1}. (M.31)

Date: 2015-09-02; view: 385; Нарушение авторских прав