Обращение квадратных матриц

Матрица A_nn^-1 называется обратной по отношению к некоторой исходной квадратной матрице A_nn, если, будучи умноженной, слева или справа, на эту исходную, она даёт единичную матрицу такого же размера:

A^-1*A = A*A^-1 = I. (M.12)

Свойства операции обращения квадратных матриц:

1) (A^-1)^-1 = A;

2) (A^-1)^T = (A^T)^-1;

3) (AB)^-1 = B^-1A^-1;

4) (αA)^-1 = 1/α*A^-1;

5) (A + B)^-1 ≠ A^-1 + B^-1.

Матрица, обратная квадратной, строится следующим образом.

1) вычисляется определитель исходной матрицы – det(A). Если det(A) ≠ 0, то A^-1 существует, а матрица A является неособенной;

2) строится союзная к A матрица, состоящая из алгебраических дополнений A_ij = (–1)^i+jM_ij, представляющих собой соответствующие миноры M_ij матрицы A, знак перед которыми определяется знаком величины (–1)^i+j; каждое алгебраическое дополнение A_ij записывается в союзную матрицу на пересечении j -ой строки с i -ым столбцом;

3) все элементы союзной матрицы делятся на определитель такой неособенной матрицы det(A).

На этом процедура получения обратной матрицы завершается.

Проиллюстрируем вышеизложенное на примере построения обратной матрицы для неособенной матрицы второго порядка

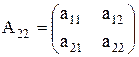. (M.13)

Найдём определитель этой матрицы:

det(A) = Δ = a₁₁*a₂₂ – a₁₂*a₂₁≠ 0. (M.14)

Далее получим алгебраические дополнения:

A₁₁ = (–1)¹⁺¹*a₂₂; A₁₂ = (–1)¹⁺²*a₂₁; A₂₁ = (–1)²⁺¹*a₁₂; A₂₂ = (–1)²⁺²*a₁₁.

Теперь сгруппируем алгебраические дополнения в союзную матрицу, разделив их на определитель Δ, и получим матрицу A^-1, обратную к исходной A:

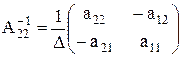(M.15)

Разобранный выше теоретически корректный путь построения обратной матрицы на практике далее матриц второго порядка не применяется. Можно найти элементы обратной матрицы с использованием разнообразных алгоритмов решения систем линейных алгебраических уравнений (СЛАУ), с которыми мы познакомимся позже.

Date: 2015-09-02; view: 344; Нарушение авторских прав