Соотношения между элементами навигационного треугольника скоростей. НТС – это обычный треугольник, поэтому к нему можно применить любые известные из тригонометрии формулы для установления связей между его элементами – углами и

НТС – это обычный треугольник, поэтому к нему можно применить любые известные из тригонометрии формулы для установления связей между его элементами – углами и сторонами.

Элементы НТС, да и любые навигационные величины, могут быть обозначены латинскими и греческими буквами (ε, βф, α и т.д.), либо русскими аббревиатурами (УВ, ФПУ, УС и т.п.). В аэронавигации все эти обозначения используются как равноправные.

Рассмотрим наиболее важные соотношения между элементами навигационного треугольника скоростей. Основным элементом треугольника, от которого в значительной степени зависят все остальные, является угол ветра. Он может быть найден из очевидного соотношения (рис. 3.3):

УВ = НВ – ФПУ

или, что то же самое

ε=δн – βф.

Если НТС решается во время подготовки к полету, когда фактического путевого угла еще нет (ведь самолет еще не летит), то вместо него используется заданный путевой угол на том основании, что для полета по ЛЗП (а именно для этого случая и рассчитывается УВ) фактический ПУ должен быть равен заданному.

При расчете по формуле УВ может оказаться отрицательным или превысить 360° В этом случае его легко привести в диапазон от 0° до 360°. Впрочем, как будет показано далее, в этом может и не быть необходимости.

Если известны курс К и ФПУ, то легко найти угол сноса УС:

УС=ФПУ – К, α = βф – γ.

и, наоборот, по известному УС найти ФПУ:

ФПУ=К + УС, βa = γ + α.

При расчете по этим и по другим аналогичным формулам необходимо помнить, что УС имеет свой собственный знак, который учитывается по правилам алгебры.

Например, если ФПУ=357°, УС= –5°, то

К = ФПУ – УС=357 – (–5)= 357+5=362=362 – 360=2°.

Эта формула может быть применяется при расчете заданного курса, то есть курса, который необходимо выдерживать пилоту, чтобы ВС летело в заданном направлении (чтобы ФПУ был равен ЗПУ).

Курсовой угол ветра КУВ и угол ветра УВ связаны простым соотношением:

КУВ=УВ+УС, ψ = ε + α.

Если и УВ и КУВ измерять не в диапазоне от 0° до 360°, а от –180° до +180°, то УВ и КУВ всегда будут иметь одинаковый знак, совпадающий со знаком УС. Это означает, что при расчете по данной формуле можно пользоваться абсолютными величинами и считать будет легче. Например, УВ=330º, УС= –5º. Тогда при формальном расчете получим:

КУВ=330º + (–5º)=325º.

Но КУВ=330= –30. Тогда, складывая модули (абсолютные величины) УВ и УС, получим:

30+5=35.

Разумеется, полученный КУВ также имеет знак минус. Но –35=325, следовательно, ответ получен тот же: КУВ=325º.

При решении НТС часто используется теорема синусов, которая гласит, что в любом треугольнике отношение стороны к синусу противолежащего угла есть величина постоянная.

Из нее можно получить полезное соотношение для определения угла сноса:

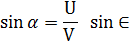
или, что то же самое:

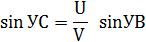
Путевая скорость может быть найдена различными способами. Например, на изображении НТС (рис. 3.6) можно заметить, что длина отрезка ОС (то есть W) складывается из длин отрезков ОВ и ВС, являющихся соответственно проекциями на направление W векторов истинной скорости V и ветра U:

W=ОВ+ВС=V cos α + U cos ε.

Рис. 3.6. К выводу соотношений в треугольнике скоростей

Поскольку УС обычно невелик, то cos α ≈ 1и тогда можно использовать приближенное соотношение:

W≈V+ U cos ε.

Date: 2015-09-02; view: 629; Нарушение авторских прав