Навигационный треугольник скоростей

ВС движется относительно воздушной массы с истинной воздушной скоростью V, воздушная масса относительно земли со скоростью U, и скорость перемещения ВС относительно земной поверхности (полная скорость) Wп является векторной суммой этих скоростей. При горизонтальном движении ВС его полная скорость практически совпадает с путевой скоростью W. Поэтому можно записать векторное соотношение:

W = V + U

В математике сумма векторов строится графически как диагональ параллелограмма, сторонами которого являются слагаемые векторы (рис.3.2). Но не обязательно строить весь параллелограмм, так как у него стороны попарно равны и параллельны, а диагональ разбивает его на два равных треугольника. Поэтому достаточно построить один такой треугольник, чтобы получить диагональ – сумму векторов. Чтобы сделать это, необходимо из конца первого слагаемого вектора, построить второй слагаемый вектор. Соединив начало первого вектора с концом второго получим вектор суммы (см. рис. 3.2)

.

Рис. 3.2. Сложение векторов по правилам параллелограмма и треугольника

Применив такой подход к векторам V и U, получим векторный треугольник, называемый навигационным треугольником скоростей (рис. 3.3).

Навигационный треугольник скоростей (НТС) – векторный треугольник, образованный векторами истинной воздушной скорости, ветра и путевой скорости..

Конфигурация навигационного треугольника скоростей может быть различной. Ведь векторы V и U могут быть направлены в любую сторону. Но соединены в треугольник они должны быть вполне определенным образом (рис.3.4). Ведь навигационный треугольник скоростей отражает то, что V и U складываются, образуя путевую скорость W как их сумму.

Рис. 3.3. Навигационный треугольник скоростей

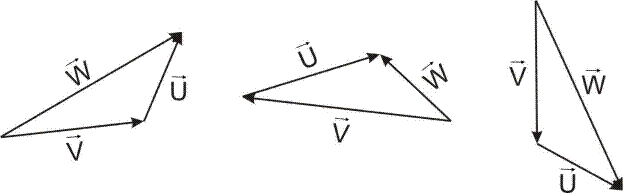
Рис. 3.4. Некоторые возможные конфигурации навигационного треугольника скоростей

На рисунке (см. рис. 3.3) НТС дан в той конфигурации, в которой его обычно изображают для ознакомления с его элементами. Элементами НТС называют его стороны, углы между ними, а также углы, которые характеризуют направление сторон треугольника (векторов скоростей) относительно меридиана.

На рисунке изображены многие элементы, которые уже рассматривались ранее:

- курс γ – угол между северным направлением меридиана и направлением вектора V (как уже упоминалось, его принято считать у самолетов направленным по продольной оси ВС);

- фактический путевой угол β_Ф – угол между северным направлением меридиана и направлением вектора W;

- навигационное направление ветра δн – угол между северным направлением меридиана и направлением вектора U.

Конечно, элементами НТС являются и модули всех трех скоростей.

Но, кроме этих элементов, появляются и новые, характеризующие углы между векторами.

Одним из таких элементом, самым важным для понимания влияния ветра на полет ВС, является угол ветра.

Угол ветра (УВ, ε) – угол, заключенный между направлениями вектора путевой скорости W и вектора ветра U.

Его принято отсчитывать от вектора W по часовой стрелке от 0˚ до 360˚. Однако на практике при решении некоторых навигационных задач его удобнее считать изменяющимся от 0˚ до ±180˚.

Необходимо обратить внимание, что УВ измеряется именно между направлениями, куда направлены векторы W и U (на рисунке эти направления показаны пунктиром). Поэтому неправильно было бы показать УВ как внутренний угол треугольника, расположенный между этими же векторами: ведь тогда это будет это угол между направлениями, противоположными направлениям W и U. В данной конфигурации НТС этот угол, конечно, численно равен УВ, но в других конфигурациях это может оказаться не так.

Не следует путать направление ветра δн и угол ветра ε. В то время как δн характеризует, куда дует ветер о тносительно меридиана (на север, восток и т.д.), угол ветра показывает, куда дует ветер относительно направления полета (вправо, влево, вперед, назад и т.д.).

Курсовой угол ветра (КУВ,ψ) – угол, заключенный между направлениями вектора истинной скорости V и вектора ветра U. Отсчитывается аналогично углу ветра: от направления, куда направлен вектор V, до направления вектора U по часовой стрелке от 0˚ до 360˚ (иногда от 0˚ до ±180˚). Название этого элемента (курсовой угол) подсказывает, от какого направления он измеряется: ведь вектор V направлен по продольной оси самолета, то есть по линии курса. Полезно запомнить, что, если измерять УВ и КУВ в диапазоне от 0˚ до ±180˚, то они всегда имеют одинаковый знак, да и по абсолютной величине отличаются друг от друга незначительно – на величину угла сноса.

Угол сноса (УС, α) – угол, заключенный между направлениями вектора истинной V и путевой W скоростей.

Отсчитывается УС от направления вектора V, которое в свою очередь совпадает с направлением продольной оси ВС. В отличие от УВ и КУВ он всегда измеряется в диапазоне от 0˚ до ±180˚: вправо (по часовой стрелке) с плюсом, влево (против часовой стрелки) с минусом. По-английски угол сноса – drift angle или кратко просто drift (снос).

Название этого элемента отражает его физический смысл. Продольная ось самолета направлена в одну сторону (в направлении вектора V), но летит ВС относительно земной поверхности несколько в другую сторону (в направлении вектора W). То есть ветер как бы сносит ВС с того направления полета, куда направлен нос ВС. Так самолет и перемещается с отвернутой от ЛФП на угол сноса продольной осью (рис. 3.5).

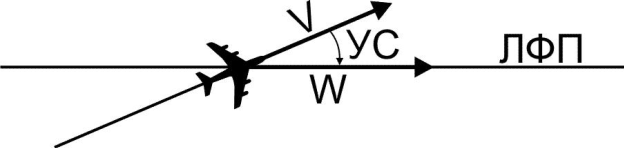
Рис. 3.5. Угол сноса

Поскольку скорость ветра обычно меньше (а часто в несколько раз меньше), чем скорость самолета, то абсолютная величина УС как правило невелика – единицы градусов. Лишь для тихоходных ВС или при очень сильном ветре УС может достигать 10-20˚.

Date: 2015-09-02; view: 1686; Нарушение авторских прав