
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Системы дифференциальных уравнений
|
|
Система дифференциальных уравнений вида
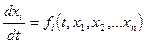 , , 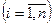
| (11.1) |
где х 1, х 2, … х n – неизвестные функции независимой переменной t, называется нормальной системой (системой в нормальной форме) или системой, разрешённой относительно производных от неизвестных функций x i = x i(t). Если правые части нормальной системы дифференциальных уравнений являются линейными функциями относительно х 1, х 2, … хn , то система дифференциальных уравнений называется линейной.
Нормальная система двух дифференциальных уравнений первого порядка записывается в виде:
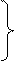
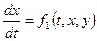
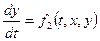 . (11.2)
. (11.2)
Решением системы (11.2) называется всякий набор из двух функций 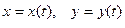 , обращающих оба уравнения системы в тождества.
, обращающих оба уравнения системы в тождества.
Задача Коши для системы (11.2) состоит в том, чтобы найти такое решение, которое при  принимало бы заданные значения:
принимало бы заданные значения:
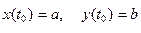 . .
| (11.3) |
Общее решение системы (11.2) содержит две произвольные постоянные С 1, С 2, фиксируя которые находят любое частное решение в области изменения начальных условий  . Неявная запись решений:
. Неявная запись решений:
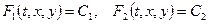 . .
| (11.4) |
Соотношения (11.4) называют первыми интегралами системы.
Геометрически решение 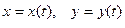 определяет некоторую линию (интегральную кривую системы) на плоскости
определяет некоторую линию (интегральную кривую системы) на плоскости 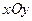 . Если считать, что аргумент t играет роль времени, то указанная кривая будет служить траекторией точки, движущейся на плоскости
. Если считать, что аргумент t играет роль времени, то указанная кривая будет служить траекторией точки, движущейся на плоскости 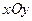 . В этом случае
. В этом случае 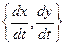 определяет вектор скорости. С механической точки зрения система (11.2) означает задание поля скоростей в каждый момент времени t, а решение задачи Коши равносильно нахождению траектории точки, движущейся под воздействием этого поля и занимающей в начальный момент времени
определяет вектор скорости. С механической точки зрения система (11.2) означает задание поля скоростей в каждый момент времени t, а решение задачи Коши равносильно нахождению траектории точки, движущейся под воздействием этого поля и занимающей в начальный момент времени  положение (a, b). Плоскость
положение (a, b). Плоскость 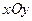 , на которой рассматривается движение, называется фазовой.
, на которой рассматривается движение, называется фазовой.
Рассмотрим два метода решения систем дифференциальных уравнений в нормальной форме.
Метод нахождения интегрируемых комбинаций
Сущность этого метода состоит в том, что с помощью арифметических операций из уравнений данной системы образуют так называемые интегрируемые комбинации, то есть легко интегрируемые уравнения относительно новой неизвестной функции.
Пример 1. Решить систему уравнений 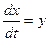 ,
, 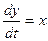 .
.
D Складывая почленно эти уравнения, находим одну интегрируемую комбинацию:
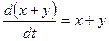 ,
, 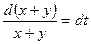 ,
, 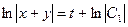 ,
,  .
.
Почленно вычитая из первого уравнения системы второе, получаем другую:
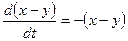 ,
, 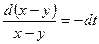 ,
, 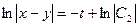 ,
, 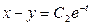
Из найденных уравнений определяем решение системы
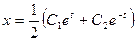 ,
,  , или
, или 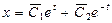 ,
, 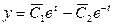
где 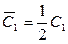 ,
, 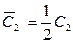 . Ñ
. Ñ
Пример 2. Решить систему уравнений 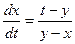 ,
, 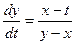 .
.
Ñ Замечаем, что при сложении уравнений системы в правой части пропадают неизвестные х и у. То же самое происходит при сложении уравнений с множителями х и у соответственно:
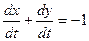 ,
, 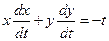
Или
dx +dy = -dt, xdx + ydy = − tdt.
Интегрируя эти равенства и перенося влево член с t, получим первые интегралы системы в виде:
x+ y +t =C 1, x 2 + y 2 + t 2 =C 2.
Отсюда можно выразить х и у через t, C 1, C 2.т.е. получить общее решение системы. Ñ
Геометрическая интерпретация. Эти интегралы в пространстве 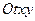 задают окружность как пересечение сферы x 2 + y 2 + t 2 =C 2 c плоскостью x+ y +t =C 1 . Проектируя эту окружность на фазовую плоскость
задают окружность как пересечение сферы x 2 + y 2 + t 2 =C 2 c плоскостью x+ y +t =C 1 . Проектируя эту окружность на фазовую плоскость 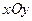 , получим на ней эллипс. Его уравнение находится исключением t из первых интегралов.
, получим на ней эллипс. Его уравнение находится исключением t из первых интегралов.
Пример 3. Решить систему уравнений 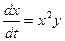 ,
, 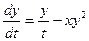 .
.
D Умножив обе части первого уравнения на у, а второго – на х и сложив почленно полученные уравнения, имеем
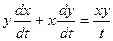 или
или  .
.
Отсюда xу =C 1 t . (*)
Вводя (*) в первое уравнение системы, получим 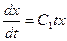 .
.
Интегрируя это уравнение, находим х:
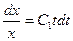 ,
, 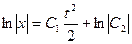 ,
, 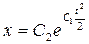 .
.
Из равенства (*) в случае 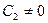 имеем
имеем 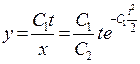 .
.
Кроме того, если у = 0, из первого уравнения системы х = С, а если х = 0, то из второго уравнения у = Сt. Ñ
Метод исключения неизвестных
Иногда нормальную систему дифференциальных уравнений удаётся привести к одному уравнению более высокого порядка, содержащему одну неизвестную функцию. Общая схема приведения состоит в следующем. Дифференцируя, например, первое из уравнений (11.1) последовательно (n- 1) раз и подставляя каждый раз вместо производных 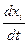 их значения, из остальных уравнений этой же системы имеем
их значения, из остальных уравнений этой же системы имеем
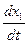 = F 1 (t, x 1, x 2,… x n), = F 1 (t, x 1, x 2,… x n),
| |
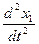 = F 2 (t, x 1, x 2,… x n), = F 2 (t, x 1, x 2,… x n),
| |
| …….…………………… | (11.5) |
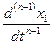 = F n-1 (t, x 1, x 2,… x n), = F n-1 (t, x 1, x 2,… x n),
| |
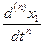 = F n (t, x 1, x 2,… x n). = F n (t, x 1, x 2,… x n).
|
Определив х 2, х 3, … х n из первых (n- 1) уравнений системы (11.5) и подставив эти выражения в последнее уравнение системы, получим дифференциальное уравнение n- ого прядка
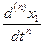 =F =F 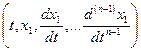 . .
| (11.6) |
Решив это уравнение, найдём решения исходной системы уравнений.
Пример 4. Решить систему уравнений  ,
, 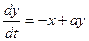 .
.
D Дифференцируя обе части первого из данных уравнений, имеем
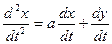 . (**)
. (**)
Из второго уравнения находим
 .
.
Подставив это выражение в (**), получим уравнение второго порядка с постоянными коэффициентами:
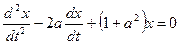 .
.
Для его решения составим и решим характеристическое уравнение:
k 2 – 2 ak +(1 +a 2) = 0, k 1,2 = a ± 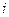 .
.
Следовательно, x = eat (C 1 cos t + C 2 sin t). Из первого уравнения исходной системы определяем y (t):
y=  − ax=aeat (C 1 cos t + C 2 sin t)+ eat (− C 1 sin t+ C 2 cos t) − aeat (C 1 cos t + C 2 sin t) = =eat (− C 1sin t + C 2 cos t). Ñ
− ax=aeat (C 1 cos t + C 2 sin t)+ eat (− C 1 sin t+ C 2 cos t) − aeat (C 1 cos t + C 2 sin t) = =eat (− C 1sin t + C 2 cos t). Ñ
Пример 5. Решить систему уравнений 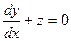 ,
, 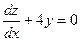
D Дифференцируя второе уравнение: 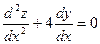 и учитывая, что, согласно первому
и учитывая, что, согласно первому 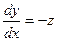 , имеем
, имеем 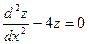 . Отсюда
. Отсюда  .
.
Далее находим 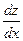 и подставляем во второе уравнение системы:
и подставляем во второе уравнение системы:
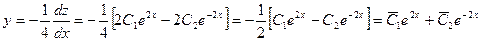 , где
, где  ,
, 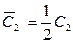 . Ñ
. Ñ
Пример 6. Решить систему уравнений 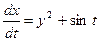 ,
, 
D Дифференцируя обе части первого из данных уравнений, имеем
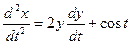 . (***)
. (***)
Из второго уравнения находим 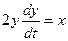 , поэтому уравнение (***) можно представить в виде
, поэтому уравнение (***) можно представить в виде 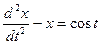 .
.
Общее решение этого уравнения:  . Из первого уравнения системы находим
. Из первого уравнения системы находим 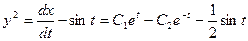 . Ñ
. Ñ
Понятие о системах линейных дифференциальных уравнений с постоянными коэффициентами
Пусть мы имеем систему дифференциальных уравнений
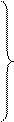
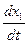 =a11x1 + a12x2 +…+a1nxn
=a11x1 + a12x2 +…+a1nxn
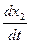 =a21x1 + a22x2+…+a2nxn (11.7)
=a21x1 + a22x2+…+a2nxn (11.7)
……………………………..…
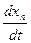 =an1x1 + an2x2+…+annxn..
=an1x1 + an2x2+…+annxn..
Здесь t – аргумент, x 1(t), x 2(t),… x n(t)- искомые функции, 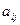 – постоянные. Система (11.7) называется системой линейных однородных дифференциальных уравнений с постоянными коэффициентами.
– постоянные. Система (11.7) называется системой линейных однородных дифференциальных уравнений с постоянными коэффициентами.
Эту систему можно решать путем сведения к одному уравнению n -ого порядка, которое в данном случае будет линейным. Но можно решать систему (11.7) и другим методом, не сводя к уравнению n- ого порядка. Рассмотрим его на примере решения системы двух уравнений
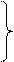
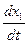 =a 11 x 1 + a 12 x 2
=a 11 x 1 + a 12 x 2
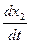 =a 21 x 1 + a22x2 (11.7а)
=a 21 x 1 + a22x2 (11.7а)
Будем искать частное решение системы в виде:
| x 1 = a 1 ek t, x 2 = a 2 ekt. | (11.8) |
Требуется определить постоянные a1, a2 и k так, чтобы функции a 1 ekt, a 2 ekt удовлетворяли системе уравнений (11.7а). Подставляя их в систему (11.7а), получаем:
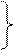 ka 1 ekt = (a 11 a 1 + a 12 a 2) ekt
ka 1 ekt = (a 11 a 1 + a 12 a 2) ekt
ka 2 ekt = (a 21 a 1 + a 22 a 2) ekt
Сократим на ekt. Перенося все члены в одну сторону и собирая коэффициенты при a 1 и a 2, получим систему уравнений:
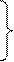 (a11- k) a1 + a12a2 = 0
(a11- k) a1 + a12a2 = 0
(11.9)
a21a 1+ (a22- k) a2 = 0
Для того чтобы эта система имела нетривиальное (ненулевое) решение, необходимо и достаточно, чтобы её определитель был равен нулю:
 a11 –k a12
a11 –k a12
=0 (11.10)
a21 a22 –k
Уравнение (11.10) называется характеристическим уравнением системы (11.9). Из уравнения (11.10) мы и получаем те значения k, при которых система (11.9) имеет нетривиальные решения.
Ограничиваясь рассмотрением случая, когда корни характеристического уравнения (k 1 и k 2) действительные и различные, на основе системы уравнений (11.9) находим
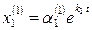 ,
, 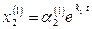
и
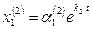 ,
, 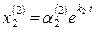 .
.
Ее общим решением является система функций
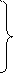
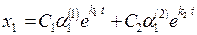 (11.11)
(11.11)
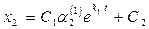
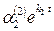
Пример 7. Решить систему уравнений 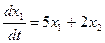 ,
, 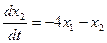 .
.
D Частные решения этой системы ищем в виде x 1 = aekt, x 2 = bekt (новые обозначения искомых постоянных ввели для удобства записи). Подставляя эти выражения в данную систему, для определения a и b получим линейную однородную систему уравнений
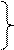 (5 − k) a+ 2 b = 0
(5 − k) a+ 2 b = 0
(*)
−4 a + (−1− k) b = 0.
Составляем характеристическое уравнение:
 5− k 2
5− k 2
=0
−4 −1− k
и находим его корни: k 1 = 1, k 2 = 3.
При k = k 1 = 1 система уравнений (*) эквивалентна уравнению 4 a + 2 b = 0, одно из решений которого есть a =1, b = −2. Поэтому x 1(1) = et, x 2(1) = −2 et являются решением исходной системы уравнений.
Подставив корень k = 3 в систему (*), получим эквивалентное ей уравнение 2 a + 2 b = 0. Одно из его решение есть a = 1, b = −1. Таким образом, найдено ещё одно решение исходной системы уравнений: x1(2) = e3t, x2(2) = −e 3t.
Поскольку
 et e 3 t
et e 3 t
= e 4 t¹ 0,
−2 et − e 3 t
найденные два решения являются линейно независимыми, а следовательно, образуют фундаментальную систему решений.
Поэтому общее решение исходной системы будет
x 1 =C 1 et + C 2 e 3 t
x2 = −2 C 1 et – C 2 e 3 t ,
где С 1 и С 2 – произвольные постоянные. Ñ
Раздел «Дифференциальные уравнения» в программе курса математики на технологических факультетах обеспечивается лишь шестью лекциями. Поэтому важно в рамках самостоятельной работы углубит и расширить полученные знания, изучить как учебную литературу, так и специальные монографии, рекомендуемые преподавателями. Очень советую познакомиться, в частности, с замечательными книгами: А.М. Смойленко, С.А. Кривошея, Н.А. Перестюк. «Дифференциальные уравнения: примеры и задачи». «Высшая школа». 1989; В.В. Амелькин. «Дифференциальные уравнения в приложениях». «Наука». ГРФМЛ. 1987.
Важно получить представление о возмодностях использования дифференциальных уравнений при изучении реальных явлений и процессов, осознать широкое использование при их составлении геометрического и физического смысла производной, а также законов естественных наук. В качестве примеров полезно рассмотреть задачи о движении точки под действием постоянной и периодической силы, а также силы, пропорциональной скорости, о колебании точки под действием упругой силы, задачу о колебаниях математического маятника.
Наконец, необходимо с методами приближенных решений, с качественной теорией дифференциальных уравнений, одним из основных вопросов которой является проблема устойчивости решения или устойчивости движения.Этот вопрос исследован в работах выдающегося русского математика А.М. Ляпунрва (1857-1918).
Желаю Вам, мои юные друзья, успехов в учебе и прошу высказать критические замечания по содержанию представленного конспекта лекций. Это очень важно для мен в деле дальнейшего совершенствования учебного процесса.
Date: 2015-09-02; view: 1101; Нарушение авторских прав