
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Линейные неоднородные уравнения второго порядка с постоянными коэффициентами
|
|
Это уравнения вида
 , ,
| (9.1) |
где 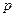 и
и 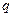 − данные постоянные числа, а
− данные постоянные числа, а 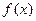 (правая часть уравнения) − известная функция от
(правая часть уравнения) − известная функция от 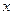 . Структура общего решения такого уравнения определяется следующей теоремой.
. Структура общего решения такого уравнения определяется следующей теоремой.
Теорема. Общее решение неоднородного уравнения (9.1) равно сумме общего решения  соответствующего однородного уравнения
соответствующего однородного уравнения
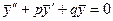
| (9.2) |
и частного решения (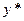 ) данного неоднородного уравнения.
) данного неоднородного уравнения.
Доказательство. Докажем, что сумма
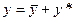
| (9.3) |
есть общее решение уравнения (9.1). Сначала установим, что функция (9.3) является решением уравнения (9.1). Подставим 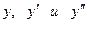 в (9.1):
в (9.1):
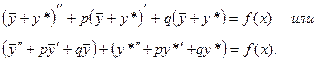
Так как 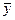 есть решение уравнения (9.2), то выражение в первых скобках
есть решение уравнения (9.2), то выражение в первых скобках
тождественно равно нулю. Далее, так как 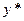 есть решение уравнения (9.1), то выражение во вторых скобках равно
есть решение уравнения (9.1), то выражение во вторых скобках равно 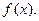 Таким образом, в результате подстановки получаем тождество, и функция (9.3)- решение уравнения (9.1)
Таким образом, в результате подстановки получаем тождество, и функция (9.3)- решение уравнения (9.1)
Докажем теперь, что выражение (9.3) есть общее решение уравнения(9.1), т.е. докажем, что входящие в него произвольные постоянные можно подобрать, чтобы удовлетворялись начальные условия, имеющие, как отмечалось выше, вид:
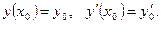
Учитывая, что
 ,
,
где 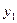 и
и  − линейно независимые решения уравнения (9.2),перепишем равенство (9.3) так:
− линейно независимые решения уравнения (9.2),перепишем равенство (9.3) так:
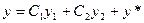 .
.
Исходя из начальных условий, имеем
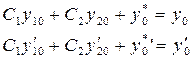 .
.
Здесь 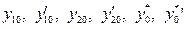 обозначают числовые значения рассматриваемых функций при
обозначают числовые значения рассматриваемых функций при 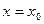 .
.
Перепишем систему уравнений в виде
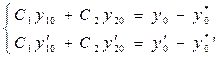 . (9.4)
. (9.4)
Ее определителем является определитель Вронского для функций 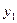 и
и  в точке
в точке 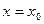 . Он отличен от нуля, так как эти функции по условию линейно независимы. Следовательно, существуют такие решения
. Он отличен от нуля, так как эти функции по условию линейно независимы. Следовательно, существуют такие решения 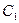 и
и 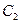 системы (9.4), при которых формула (9.3) определяет решение уравнения (9.1), удовлетворяющее данным начальным условиям.
системы (9.4), при которых формула (9.3) определяет решение уравнения (9.1), удовлетворяющее данным начальным условиям.
Теорема доказана.
Таким образом, чтобы найти общее решение линейного неоднородного уравнения, нужно найти общее решение соответствующего однородного уравнения (для этого используем результаты изложенного выше пункта 8) и какое-нибудь частное решение неоднородного уравнения. Вид частного решения уравнения (9.1) зависит от вида правой части этого уравнения.
Лекция 11.
10. Методы нахождения частных решений неоднородных линейных уравнений второго порядка с постоянными коэффициентами
В общем случае задача нахождения частного решения неоднородного уравнения (9.1) является сложной. Можно получить решение методом вариации постоянных, если известно общее решение соответствующего однородного уравнения (9.2).
 . .
| (10.1) |
Будем искать частное решение неоднородного уравнения в форме (10.1), рассматривая С 1 и С 2 как некоторые искомые функции от х:
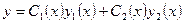 . .
| (10.2) |
Продифференцируем это равенство
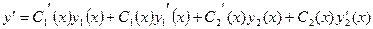 . .
| (10.3) |
Подберем искомые функции С 1(х) и С 2 (х) так, чтобы выполнялось равенство
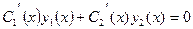 . .
| (10.4) |
С учетом этого дополнительного условия первая производная 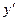 принимает вид
принимает вид
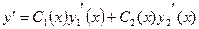 .
.
Дифференцируя это равенство, найдем 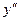 :
:
 .
.
Подставляя 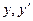 и
и 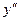 в уравнение (9.1) и группируя слагаемые, получаем
в уравнение (9.1) и группируя слагаемые, получаем 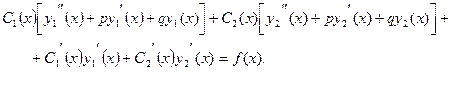
Выражения, стоящие в скобках, равны нулю, так как 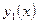 и
и 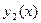 - решения однородного уравнения. Следовательно, последнее равенство принимает вид
- решения однородного уравнения. Следовательно, последнее равенство принимает вид
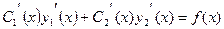 . .
| (10.5) |
Таким образом, функция (10.2) является решением уравнения (9.1), если функции С 1(х) и С 2 (х) удовлетворяют системе уравнений (10.4) и (10.5):

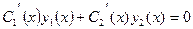 (10.6)
(10.6)
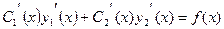 .
.
Эта система имеет единственное решение относительно  и
и 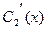 , так как ее определителем является определитель Вронского для линейно независимых решений
, так как ее определителем является определитель Вронского для линейно независимых решений 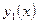 и
и 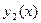 однородного уравнения (9.2). Согласно теореме о структуре общего решения этого уравнения, он не равен нулю. Решая систему (10.6), находим
однородного уравнения (9.2). Согласно теореме о структуре общего решения этого уравнения, он не равен нулю. Решая систему (10.6), находим
 и
и 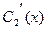 как определенные функции от х:
как определенные функции от х:
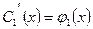 ,
, 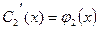 .
.
Интегрируя, найдем 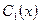 и
и 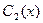 :
:
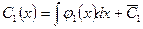 ,
, 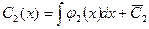 ,
,
где 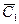 и
и  − постоянные интегрирования. Подставляя полученные выражения для
− постоянные интегрирования. Подставляя полученные выражения для 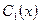 и
и 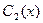 в равенство (10.2), получаем искомое частное решение уравнения (9.1) (при
в равенство (10.2), получаем искомое частное решение уравнения (9.1) (при 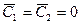 ).
).
Пример 1. Найти частное решение уравнения  .
.
D Общее решение соответствующего однородного уравнения 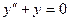 определяется выражением
определяется выражением
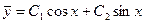 .
.
Поэтому частное решение исходного неоднородного уравнения будем искать в виде (варьируем С1 и С2 )
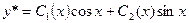 .
.
Система (10.6) для нахождения  и
и 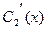 в данном случае записывается так:
в данном случае записывается так:

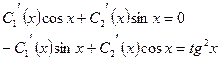 .
.
Отсюда
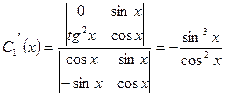 ;
; 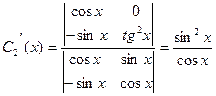 .
.
В результате интегрирования получаем 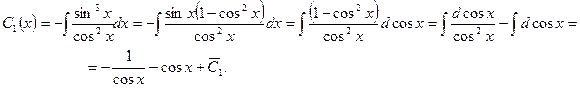
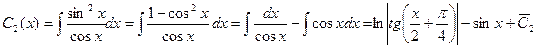 .
.
Подставляя 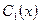 и
и 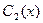 в выражение для у*, произвольные постоянные не пишем, так как ищем частное решение
в выражение для у*, произвольные постоянные не пишем, так как ищем частное решение 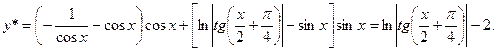
Зная общее решение соответствующего однородного уравнения, можем записать общее решение рассмотренного неоднородного уравнения
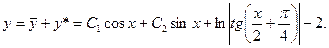 Ñ
Ñ
Пример 2. Найти частное решение уравнения 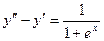 .
.
D В данном случае  . Поэтому ищем у* в виде
. Поэтому ищем у* в виде 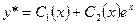 .
.
Согласно (10.6), имеем

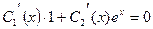
 .
.
Решая систему, находим
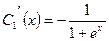 ,
,  .
.
Отсюда 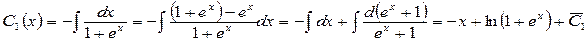
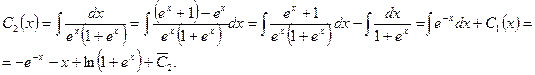
Таким образом, частное решение исходного уравнения имеет вид:
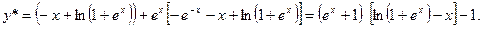 Ñ
Ñ
Если правая часть уравнения (9.1) содержит многочлен, либо показательную функцию, либо тригонометрическую функцию  или
или 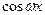 , то частное решение может быть найдено методом неопределенных коэффициентов, не содержащим процесса интегрирования.
, то частное решение может быть найдено методом неопределенных коэффициентов, не содержащим процесса интегрирования.
Рассмотрим различные виды правых частей уравнения (9.1) 
Случай I. Правая часть представляет собой полином, например, второй степени
 (10.7)
(10.7)
Если 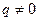 , то частное решение у * уравнения (9.1) ищется также в форме квадратного трехчлена:
, то частное решение у * уравнения (9.1) ищется также в форме квадратного трехчлена:  , где
, где 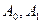 и
и 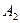 - неопределенные коэффициенты. Дифференцируя дважды y *:
- неопределенные коэффициенты. Дифференцируя дважды y *:  ,
, 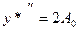 и подставляя эти выражения в уравнение (9.1), в котором
и подставляя эти выражения в уравнение (9.1), в котором 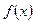 определяется (10.7), получим:
определяется (10.7), получим:
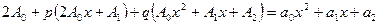
или
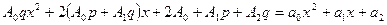 .
.
Сравнивая коэффициенты при одинаковых степенях x в обеих частях равенства, имеем:
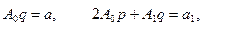
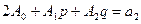 (10.8)
(10.8)
Так как 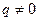 , то из этой системы для коэффициентов
, то из этой системы для коэффициентов 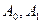 и
и 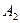 получаются определенные числовые значения. Тем самым частное решение y * будет вполне определено.
получаются определенные числовые значения. Тем самым частное решение y * будет вполне определено.
Если же 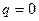 (характеристическое уравнение имеет простой нулевой корень), то система(10.8) несовместна. В этом случае частное решение, полагая, что
(характеристическое уравнение имеет простой нулевой корень), то система(10.8) несовместна. В этом случае частное решение, полагая, что 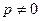 , следует искать в форме
, следует искать в форме  .
.
Аналогично обстоит дело, если 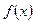 есть полином какой-нибудь другой степени, например,
есть полином какой-нибудь другой степени, например,  или
или 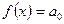 .
.
Пример 3. Решить уравнение 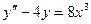 .
.
D Однородное уравнение здесь следующее
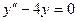 .
.
Характеристическое уравнение 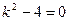 имеет корни
имеет корни 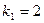 и
и 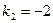 . Следовательно, общее решение однородного уравнения есть
. Следовательно, общее решение однородного уравнения есть 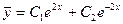
Частное решение данного уравнения ищем в виде  .
.
Находим  ,
, 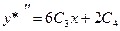 .
.
Подставив эти выражения в исходное уравнение, получим
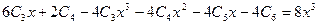 , откуда
, откуда
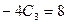 ,
, 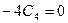 ,
, 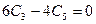 ,
, 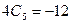 ,
, 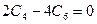 .
.
Следовательно, 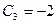 ,
, 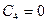 ,
, 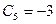 ,
, 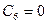 , т.е.
, т.е. 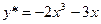 ,
,
а общее решение данного уравнения будет
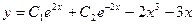 . Ñ
. Ñ
Пример 4. Решить уравнение 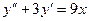 .
.
D Имеем  ,
, 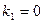 ,
, 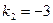 ,
, 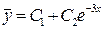 .
.
Так как 0- однократный корень характеристического уравнения, то частное решение данного уравнения ищем в виде 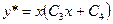 . Далее решение идет, как в предыдущем примере:
. Далее решение идет, как в предыдущем примере: 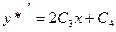 ,
, 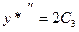 ,
,  ,
,
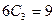 ,
, 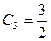 ,
,  ,
, 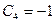 .
.
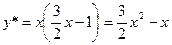 ,
, 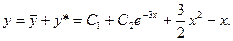 Ñ
Ñ
Случай II. Правая часть линейного неоднородного уравнения (9.1) есть показательная функция
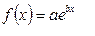
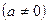 . (10.9)
. (10.9)
Ищем частное решение также в форме показательной функции  ,
,
где A -неопределенный коэффициент, отсюда 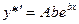
 .
.
Подставляя 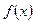 и выражения для
и выражения для 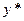 и его производных в уравнение (9.1), получим
и его производных в уравнение (9.1), получим
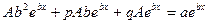 , или после сокращения на
, или после сокращения на 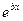 :
:
 . (10.10)
. (10.10)
Если 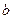 не является корнем характеристического уравнения, то
не является корнем характеристического уравнения, то
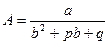 и, следовательно,
и, следовательно, 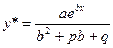 .
.
Если число 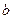 есть корень характеристического уравнения, т.е.
есть корень характеристического уравнения, т.е.  , то уравнение (10.10) противоречиво и, следовательно, уравнение (9.1) не имеет частного решения в форме (10.9).
, то уравнение (10.10) противоречиво и, следовательно, уравнение (9.1) не имеет частного решения в форме (10.9).
В этом случае, если 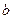 есть простой корень характеристического уравнения (т.е. другой корень отличен от
есть простой корень характеристического уравнения (т.е. другой корень отличен от 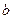 ), то частное решение ищется в форме
), то частное решение ищется в форме  . Если же
. Если же 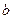 -двукратный корень характеристического уравнения, то частное решение уравнения (9.1) нужно искать в виде
-двукратный корень характеристического уравнения, то частное решение уравнения (9.1) нужно искать в виде 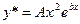 .
.
Пример 5. Пусть  .
.
D Решаем уравнение без правой части: 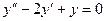 . Характеристическое уравнение имеет равные корни
. Характеристическое уравнение имеет равные корни  , и общее решение однородного уравнения:
, и общее решение однородного уравнения: 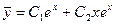 . Так как
. Так как 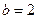 не является корнем характеристического уравнения, то ищем решение уравнения с правой частью в следующей форме:
не является корнем характеристического уравнения, то ищем решение уравнения с правой частью в следующей форме: 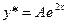 , где
, где 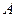 -неопределенный коэффициент. Дифференцируя, будем иметь
-неопределенный коэффициент. Дифференцируя, будем иметь  ,
, 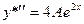 . Подставляя эти выражения в исходное уравнение, получим
. Подставляя эти выражения в исходное уравнение, получим
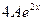 -
- 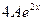 +
+ 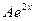 =
= 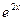 . Отсюда
. Отсюда 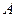 =1. Итак, частное решение уравнения с правой частью есть
=1. Итак, частное решение уравнения с правой частью есть 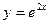 . Общее же решение этого уравнения имеет вид
. Общее же решение этого уравнения имеет вид
 . Ñ
. Ñ
Пример 6. Решить уравнение 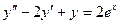 .
.
D Как и в предыдущем примере, 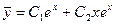 . Но в данном уравнении
. Но в данном уравнении 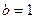 -двукратный корень характеристического уравнения. Поэтому частное решение ищем в виде:
-двукратный корень характеристического уравнения. Поэтому частное решение ищем в виде: 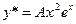 . Далее имеем:
. Далее имеем: 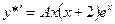 ,
, 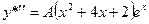 ,
, 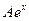
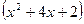 -
- 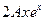
 +
+ 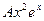 =
= 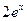 ,
, 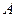 =1. Следовательно,
=1. Следовательно, 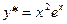
и 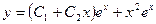 . Ñ
. Ñ
Случай III. Правая часть неоднородного уравнения (9.1) есть тригонометрический
полином
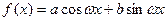 , (10.11)
, (10.11)
где 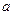 и
и 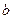 не нули одновременно.
не нули одновременно.
Ищем частное решение у * этого уравнения также в форме тригонометрического полинома 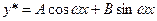 (
(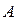 и
и 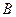 -неопределенные коэффициенты).
-неопределенные коэффициенты).
Дифференцируя, получим
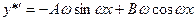 и
и  .
.
Подставляя эти выражения в уравнение (9.1) и собирая вместе члены с 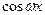 и
и  , получим:
, получим:
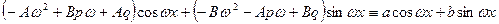 .
.
Последнее равенство представляет собой тождество, и коэффициенты при 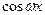 и
и  в обеих частях этого равенства должны быть соответственно равны друг другу. Поэтому
в обеих частях этого равенства должны быть соответственно равны друг другу. Поэтому
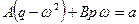 ,
,  . (10.12)
. (10.12)
Из этой системы определяются коэффициенты 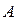 и
и 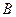 .
.
Единственный случай, когда система (10.12) несовместна, это 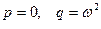 ,
,
т.е. когда  - корни характеристического уравнения. Тогда частное решение у * ищется в виде
- корни характеристического уравнения. Тогда частное решение у * ищется в виде
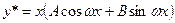 .
.
Пример 7. Пусть 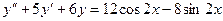 .
.
D Соответствующее однородное уравнение будет 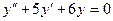 .
.
Решая характеристическое уравнение 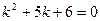 , находим корни
, находим корни
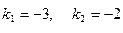 . Следовательно, общее решение однородного уравнения есть
. Следовательно, общее решение однородного уравнения есть
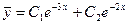 . Будем искать частное решение неоднородного уравнения в форме
. Будем искать частное решение неоднородного уравнения в форме
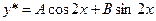 .
.
Дифференцируя, получим
 ,
, 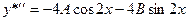
Подставляя 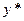 ,
, 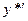 и
и 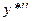 в исходное уравнение, будем иметь
в исходное уравнение, будем иметь
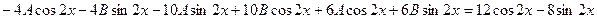
Приравнивая коэффициенты при 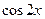 и
и 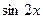 справа и слева, получим систему
справа и слева, получим систему
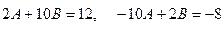 .
.
Решая эти уравнения совместно, находим 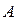 =1,
=1, 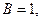 и, следовательно,
и, следовательно,  . Отсюда общее решение неоднородного уравнения будет иметь вид
. Отсюда общее решение неоднородного уравнения будет иметь вид 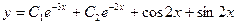 . Ñ
. Ñ
Пример 8. Найти общее решение уравнения 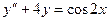 .
.
D Имеем 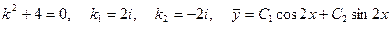 . Так как
. Так как  (
( - корни характеристического уравнения), то частное решение данного уравнения ищем в виде:
- корни характеристического уравнения), то частное решение данного уравнения ищем в виде: 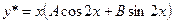 .
.
Далее имеем
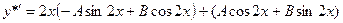 ,
,
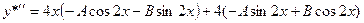 .
.
Подставляя эти выражения производных в данное уравнение и приравнивая коэффициенты при 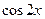 и
и 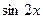 :
:
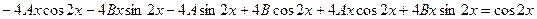 ,
,
получаем 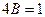 , −4
, −4 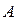 =0, т.е.
=0, т.е. 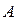 =0,
=0, 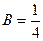 .
.
Таким образом, общее решение данного уравнения:
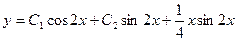 . Ñ
. Ñ
В заключение рассмотрим теорему, которую применяют при решении линейных неоднородных уравнений, в правой части которых линейная комбинация функций, указанных в случаях I-III.
Теорема. Если 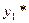 − решение уравнения
− решение уравнения
 , (9.1 а)
, (9.1 а)
а 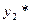 - решение уравнения
- решение уравнения
 , (9.1 б)
, (9.1 б)
то сумма 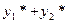 является решением уравнения
является решением уравнения

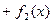 . (9.1 в)
. (9.1 в)
Доказательство. Составим сумму 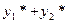 и подставим ее в левую часть
и подставим ее в левую часть
уравнения (9.1 в). Получим
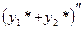 +
+ 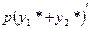 +
+ 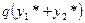 =
=
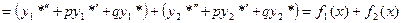 ,
,
так как по условию выражение в первой скобке равно f 1(x), а выражение во второй скобке равно 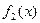 . Следовательно
. Следовательно 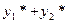 - решение уравнения (9.1 в).
- решение уравнения (9.1 в).
Теорема доказана.
Пример 9. Решить уравнение 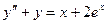 .
.
D Характеристическое уравнение 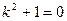 имеет корни
имеет корни  .
.
Поэтому общее решение соответствующего однородного уравнения
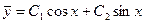 .
.
Так как правая часть состоит из суммы двух функций 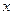 и
и 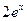 , то, в соответствии с доказанной теоремой, частное решение данного уравнения ищем в виде:
, то, в соответствии с доказанной теоремой, частное решение данного уравнения ищем в виде:
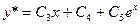 .
.
Имеем 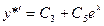 ,
, 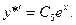
Подставляя  и
и 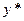 в исходное уравнение, получаем
в исходное уравнение, получаем
 .
.
Отсюда 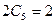 , т.е.
, т.е. 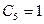 ,
, 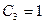 ,
, 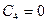 .
.
Общее решение уравнения имеет вид:
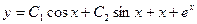 . Ñ
. Ñ
Date: 2015-09-02; view: 518; Нарушение авторских прав