
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Оценивание погрешностей
|
|
Обобщенный алгоритм оценки погрешности МВИ приведен в РМГ 62-2003 [10, п. 5-6] и состоит в следующем (рисунок 3).
 |
Рисунок 3 – Обобщенный алгоритм оценки погрешности МВИ
Рекомендации по расчету общей погрешности измерений.
1. Все составляющие погрешности исходно представляют с помощью одной из форм:
а) 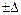 – предел абсолютной погрешности;
– предел абсолютной погрешности;
б) 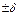 – предел относительной погрешности;
– предел относительной погрешности;
в) 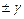 – предел приведенной погрешности;
– предел приведенной погрешности;
г) s – стандартное отклонение.
2. Для суммирования погрешностей используют пределы относительной погрешности.
3. Для перевода к относительной форме записи погрешности следует использовать следующие выражения.
Перевод форм а) → б):
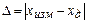 ,
, 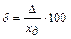 ,
,
где 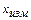 ,
, 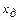 – измеренное и действительное значение измеряемой величины.
– измеренное и действительное значение измеряемой величины.
Перевод форм в) → б):
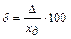 ,
, 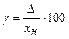 , отсюда
, отсюда 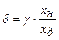 ,
,
где 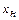 – нормирующее значение измеряемой величины – верхний предел или диапазон измерений СИ.
– нормирующее значение измеряемой величины – верхний предел или диапазон измерений СИ.
Перевод форм г) → б):
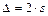 при P = 95 % (обычные измерения),
при P = 95 % (обычные измерения),
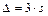 при P = 99 % (высокоточные измерения),
при P = 99 % (высокоточные измерения),
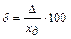 .
.
4. Суммируют составляющие погрешности по формуле
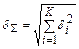 ,
,
где К – число составляющих погрешности.
5. Составляющая j -я погрешности признается существенной, если квадрат ее относительной погрешности больше 20% от квадрата общей относительной погрешности, т.е.
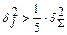 .
.
6. Получение дополнительной информации о существенных составляющих погрешности строится на более детальном рассмотрении этих составляющих.
7. Для обработки результатов и оценки погрешности прямых многократных и однократных измерений, а также косвенных измерений можно использовать соответственно ГОСТ 8.207-76 [12], Р 50.2.038-2004 [13] и МИ 2083-90 [14].
В качестве примера рассмотрим порядок обработки результатов прямых многократных измерений (выписка из ГОСТ 8.207-76 [12]).
1. Устранить влияние анормальных результатов наблюдений в случае их присутствия. Для этих целей можно использовать критерий Шовене (см. ниже).
2. За результат измерения принять среднее значение результатов N наблюдений:
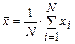 .
.
3. Вычислить стандартное отклонение результата измерений
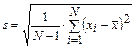 .
.
4. Определить принадлежность результатов наблюдений к нормальному закону распределения. Для этих целей можно воспользоваться критерием Пирсона или c2 (см. ниже).
5. Вычислить доверительный интервал для случайной составляющей погрешности
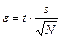 .
.
При этом взять доверительную вероятность P = 95%. Здесь t – переменная распределения Стьюдента.
6. Вычислить не исключенную систематическую погрешность результата измерения Q, которая образуется из не исключенных составляющих метода, средств и субъекта измерений и вычисляется как
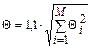 ,
,
где Q I – i -я не исключенная систематическая составляющая;
M – число составляющих погрешности.
7. Вычислить доверительный интервал общей погрешности результата измерения.
Если 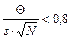 , то общая погрешность равна D = e.
, то общая погрешность равна D = e.
Если 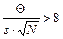 , то общая погрешность принимается равной D = Q.
, то общая погрешность принимается равной D = Q.
Если оба неравенства не выполняются, то общую погрешность результата находят по формуле
 ,
,
где К – коэффициент, зависящий от соотношения случайной и неисключенной систематической погрешностей,  – оценка суммарного среднеквадратического отклонения результата измерения
– оценка суммарного среднеквадратического отклонения результата измерения
 ,
, 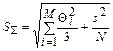 .
.
8. Записать результат измерений в виде 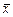 ± D, P.
± D, P.
При отсутствии данных о виде функции распределения составляющих погрешности результат измерений можно представить в виде 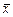 , s, N, Q, P.
, s, N, Q, P.
Критерий Шовене предназначен для анализа анормальных результатов измерений. Допустим, что результат одного или нескольких измерений значительно расходится со всеми остальными (анормальный результат). Необходимо решить, что это:
- следствие ошибки и данный результат измерений должен быть отброшен;
- законный результат, который должен рассматриваться наряду с другими.
Например, проведено N = 6 измерений и получены следующие результаты:
| 3,8 | 3,5 | 3,9 | 3,9 | 3,4 | 1,8. |
Видно, что значение 1,8 сильно отличается от остальных, и мы должны решить, что с ним делать: исключить или рассматривать наряду с другими.
Порядок использования критерия Шовене.
1. Вычисляем среднее значение  и стандартное отклонение s. Получим соответственно
и стандартное отклонение s. Получим соответственно  = 3,4 и s = 0,8.
= 3,4 и s = 0,8.
2. Вычисляем число стандартных отклонений, на которое подозрительный результат отличается от среднего значения
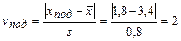 .
.
3. Предположим, что результаты измерений подчиняются нормальному закону распределения (рисунок 4), что справедливо в большинстве случаев.
Определяем по таблице вероятность того, что любой единичный результат измерений будет лежать вне ± vпод стандартных отклонений от среднего значения. Имеем в нашем случае для vпод = 2 значение P = 5 %.
| ±vпод | ||||
| P, % |
4. Находим вероятность появления результата измерений, столь же плохого, как подозрительное значение. Так как проведено не одно, а N измерений, то получим
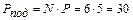 %.
%.
5. Если полученное значение вероятности меньше 50%, то подозрительное значение следует отбросить. Таким образом, результат 1,8 следует исключить из дальнейших расчетов.
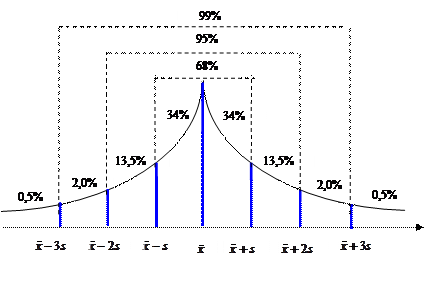
Рисунок 4 – Вероятность распределения результатов единичных
измерений в рамках нормального закона
Критерий Пирсона или c2 используют для проверки согласия наблюдаемого распределения результатов измерений с теоретическим. Допустим, проведено N = 25 измерений некоторой величины и получены следующие результаты:
| 9,9 | 11,3 | 9,9 | 9,6 | 8,6 | 11,1 | 12,5 | 10,4 | 6,8 |
| 10,0 | 10,5 | 10,4 | 10,2 | 7,5 | 10,7 | 8,3 | 11,8 | 10,4 |
| 10,5 | 13,1 | 8,4 | 11,9 | 9,3 | 9,6 | 8,1 |
Необходимо проверить, подчиняются ли полученные результаты измерений нормальному закону распределения. Для сравнения воспользуемся теоретическим процентным распределением результатов измерений, приведенным на рисунке 4.
Порядок использования критерия Пирсона.
1. Находим среднее значение и стандартное отклонение результатов измерений. Получим соответственно 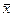 =10,0 и s = 1,5.
=10,0 и s = 1,5.
2. Разбиваем диапазон возможных значений результатов измерений на несколько бинов (интервалов). Для простоты ограничимся разбиением на 4 бина, как показано в таблице.
| Номер бина, k | ||||
| Значения в бине | x <  – s
x < 8,5 – s
x < 8,5
|  – s < x < – s < x <  8,5 < x < 10
8,5 < x < 10
|  < x < < x < 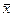 + s
10 < x < 11,5 + s
10 < x < 11,5
| x >  + s
x > 11,5 + s
x > 11,5
|
| Практическое число наблюдений в бине, О k | ||||
| Теоретическая вероятность попадания в бин, Р к % | ||||
| Теоретическое число наблюдений в бине, E k | 8,5 | 8,5 |
3. Подсчитываем число результатов измерений, которые попадают в каждый бин O k.
4. Находим, согласно рисунку 4, что теоретические вероятности попадания результатов измерений в соответствующие бины будут равны 16; 34; 34 и 16%.
5. Рассчитываем теоретическое число попаданий результатов измерений в каждый из бинов E k:
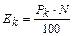 .
.
6. Определим, насколько хорошо теоретические значения попаданий E k согласуются с соответствующими наблюдаемыми значениями O k. Для оценки степени согласия вычисляется число, называемое c2:
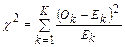 ,
,
где К – число бинов.
7. Если c2 = 0, то согласие идеальное, что практически невероятно. На практике считают, что если c2 ≤ К, то практическое и теоретическое распределения согласуются.
В нашем примере получим
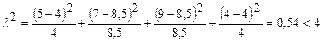 ,
,
т.е. приведенные результаты измерений подчиняются нормальному закону распределения.
Date: 2015-08-15; view: 495; Нарушение авторских прав