
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Зауваження 1
|
|
З означення випливає, що точками екстремуму можуть бути тільки внутрішні точки області визначення функції. Крім того, екстремум – це локальна (місцева) властивість функції, яка характеризує поведінку функції в досить малому околі точки. Через це їх інколи називають локальний максимум та мінімум функції.
· О! Точки х, в яких 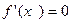 називають стаціонарними точками функції
називають стаціонарними точками функції 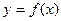 .
.
· Екстремум функції може існувати також в точках, де функція неперервна, але не має похідної.
· О! Внутрішні точки області визначення, в яких похідна не існує, називаються критичними точками.
· Точки екстремуму функції слід шукати серед її критичних точок. Якщо критичних точок немає, то функція не має і екстремумів. Однак, питання про те чи є задана критична точка точкою екстремуму вимагає додаткового дослідження за допомогою достатніх умов екстремуму функції.
Т! (перша достатня ознака екстремуму функції).
Нехай функція 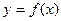 неперервна в точці х0. Якщо
неперервна в точці х0. Якщо 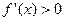 на інтервалі
на інтервалі 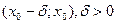 і
і  на інтервалі
на інтервалі 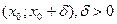 , то точка х0 є точкою максимуму функції
, то точка х0 є точкою максимуму функції 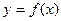 .
.
Якщо  на інтервалі
на інтервалі 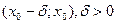 і
і 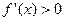 на інтервалі
на інтервалі 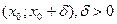 , то точка х0 є точкою мінімуму функції
, то точка х0 є точкою мінімуму функції 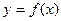 .
.
Іншими словами: Якщо при переході через точку х0 похідна змінює знак з “+” на “-“, то х0 є точкою максимуму. Якщо при переході через точку х0 похідна змінює знак з “-” на “+“, то х0 є точкою мінімуму.
Перший алгоритм дослідження функції на екстремум на інтервалі (а;в)
1. Знайти область визначення функції.
2. Знайти критичні точки функції 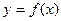 , тобто точки, в яких
, тобто точки, в яких 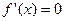 або
або 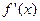 не існує і які належать інтервалу
не існує і які належать інтервалу 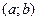 . Якщо таких точок немає, то функція екстремумів не має.
. Якщо таких точок немає, то функція екстремумів не має.
3. Дослідити знак похідної 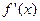 спочатку ліворуч, а потім праворуч від кожної критичної точки.
спочатку ліворуч, а потім праворуч від кожної критичної точки.
· Якщо при переході х через критичну точку х0 похідна змінює знак з “+” на “-“, то в цій критичній точці функція 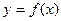 має максимум.
має максимум.
· Якщо при переході х через критичну точку х0 похідна змінює знак з “-” на “+“, то в цій критичній точці функція 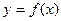 має мінімум.
має мінімум.
· Якщо при переході х через критичну точку х0 похідна не змінює знака, то в цій критичній точці функція не має ні максимуму ні мінімуму.
4. Обчислити значення функції в точках екстремуму.
Т! (друга достатня ознака екстремуму функції).
Якщо х0 – стаціонарна точка функції 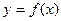 та
та 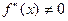 , то в точці х0 функція має екстремуму, причому максимум, якщо
, то в точці х0 функція має екстремуму, причому максимум, якщо 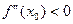 і мінімум, якщо
і мінімум, якщо 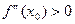 .
.
Другий алгоритм дослідження функції на екстремум на інтервалі (а; в)
1. Знайти область визначення функції.
2. Знайти стаціонарні точки функції 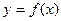 з рівняння
з рівняння 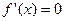 які належать інтервалу
які належать інтервалу 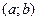 . Якщо таких точок немає, то функція екстремумів не має.
. Якщо таких точок немає, то функція екстремумів не має.
3. Знайти 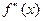 і її значення у кожній стаціонарній точці. Якщо
і її значення у кожній стаціонарній точці. Якщо 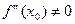 , то х0 –точка мінімуму функції
, то х0 –точка мінімуму функції 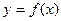 , коли
, коли 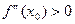 і х0 –точка максимуму функції
і х0 –точка максимуму функції 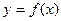 , коли
, коли 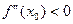 . Якщо
. Якщо 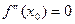 , то необхідно скористатись першим алгоритмом.
, то необхідно скористатись першим алгоритмом.
4. Обчислити значення функції в точках екстремуму.
Алгоритм знаходження найбільшого і найменшого значень функції f,
яка має на відрізку [a;b] скінчену кількість критичних точок:
1. Знайти область визначення функції.
2. Знайти критичні точки функції 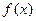 на інтервалі [a;b].
на інтервалі [a;b].
3. Обчислити значення функції 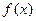 у критичних точках.
у критичних точках.
4. Обчислити  і
і  .
.
5. Серед знайдених значень функції вибрати найбільше і найменше.
Це і будуть найбільше:  , та найменше:
, та найменше: 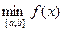 значення функції на відрізку [a;b].
значення функції на відрізку [a;b].
Т е о р е м а 1 (достатня ознака опуклості графіка функції).
Нехай функція f має на інтервалі (a;b) похідну 2-го порядку 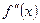 . Тоді:
. Тоді:
1) якщо  , то графік функції f опуклий вгору на цьому інтервалі;
, то графік функції f опуклий вгору на цьому інтервалі;
2) якщо 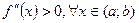 , то графік функції f опуклий вниз на цьому інтервалі.
, то графік функції f опуклий вниз на цьому інтервалі.
Інтервали, в яких графік функції опуклий вгору або вниз, називають інтервалами опуклості графіка функції.
Загальна схема дослідження функції.
1. Область визначення функції (область значень).
2. Парність, непарність функції(симетричність графіка).
3. Періодичність.
4. Асимптоти:
· вертикальні (в точках розриву ОДЗ 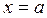 );
);
· горизонтальні: 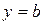 , де
, де 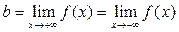 ;
;
· похилі: 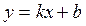 , де
, де 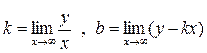 .
.
5. Перетин з осями координат:
· З віссю 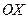 :
: 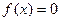 ;
;
· З віссю  :
: 
6. Дослідження функції за допомогою похідної:
· похідна функції 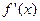
· критичні точки 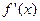 =0 або
=0 або 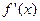 не існує.
не існує.
· проміжки монотонності: 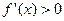 - зростає;
- зростає;  - спадає
- спадає
· точки екстремуму  ; екстремуми
; екстремуми 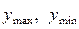 .
.
7. Дослідження функції на опуклість (точки перегину)
· друга похідна функції: 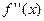
· визначаємо точки, в яких 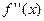 =0 або не існує, які належать інтервалу
=0 або не існує, які належать інтервалу 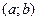 ; якщо таких точок немає, то функція точок перегину немає.
; якщо таких точок немає, то функція точок перегину немає.
· визначити чи змінює знак 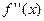 при переході через ці точки;
при переході через ці точки;
· якщо 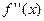 змінює знак, то встановити інтервали опуклості.
змінює знак, то встановити інтервали опуклості.
8. Додаткові точки.
| Таблиця невизначених інтегралів |
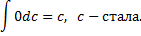
|
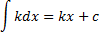
|
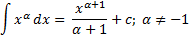
|
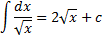
|
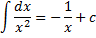
|
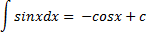
|

|
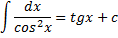
|
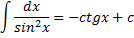
|
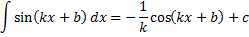
|
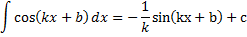
|

|

|
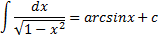
|
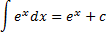
|
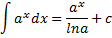
|

|

|
Основні властивості визначних інтегралів
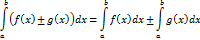
|
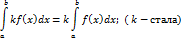
|

|
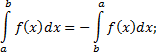
|
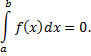
|
Медіана, яку проведено до гіпотенузи
У прямокутному трикутнику довжина медіани, що виходить з вершини прямого кута, дорівнює половині довжини гіпотенузи.
Якщо в трикутнику довжина медіани дорівнює половині довжини основи, до якої її проведено, то цей трикутник прямокутний.
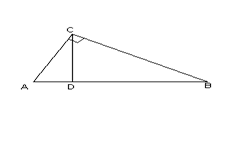 Співвідношення в прямокутному трикутнику
Співвідношення в прямокутному трикутнику
У прямокутному 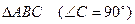 CD - висота, мають місце співвідношення:
CD - висота, мають місце співвідношення:
1)  3)
3) 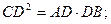
2)  4)
4) 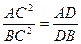 .
.
Date: 2015-08-15; view: 396; Нарушение авторских прав