
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Целая и дробная часть числа
|
|
 - целая часть числа
- целая часть числа 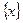 - дробная часть числа
- дробная часть числа
-
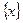 = х -
= х - 
- 0

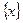 < 1
< 1 - Если х
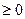 , то
, то 
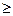 0; если х < 0, то
0; если х < 0, то  <
<  0
0 - Если p – целое число, то
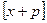 =
= 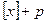
-
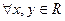 выполняется
выполняется 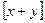
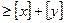 , аналогично для
, аналогично для 

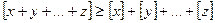
- Если
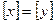 , то
, то 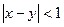
- Для любого натурального числа
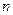 :
: 
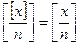
-


-
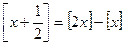
-
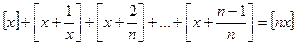 ,
, 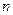 - натуральное число
- натуральное число -
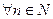 выполняется:
выполняется: 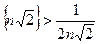
-
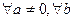 уравнение
уравнение  имеет
имеет 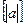 или
или  решений.
решений.
Основні властивості модуля.
-
 ;
; -
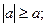
-
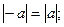
-
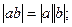
-
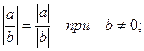
-
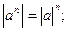
-
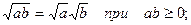
-

-
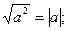
-
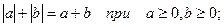
-

-

-

-
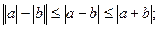
-
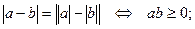
-
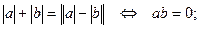
-
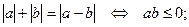
-
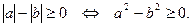

Схеми розв’язування основних типів рівнянь та нерівностей з модулем:
1. 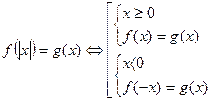
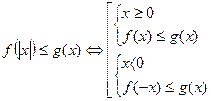
2.  або
або 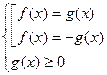
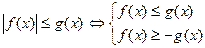
3. 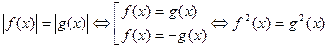
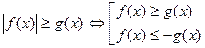
4. 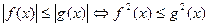
Схеми розв’язування основних типів ірраціональних рівнянь та нерівностей.
Рівняння 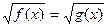 рівносильне кожній з двох систем:
рівносильне кожній з двох систем:
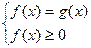 та
та 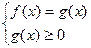
Рівняння  рівносильне системі:
рівносильне системі: 
Нерівності:
1. 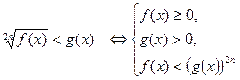 2.
2. 
3. 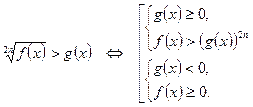 4.
4. 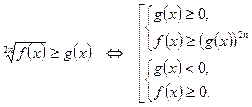
5. 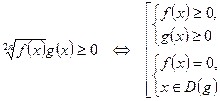 6.
6. 
7. 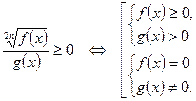 8.
8. 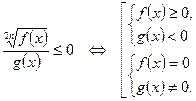
9. 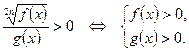 10.
10. 
11. 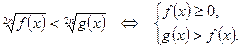
12. 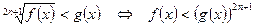
13. 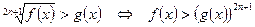
14. 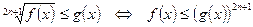
15. 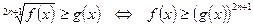
16. 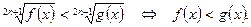
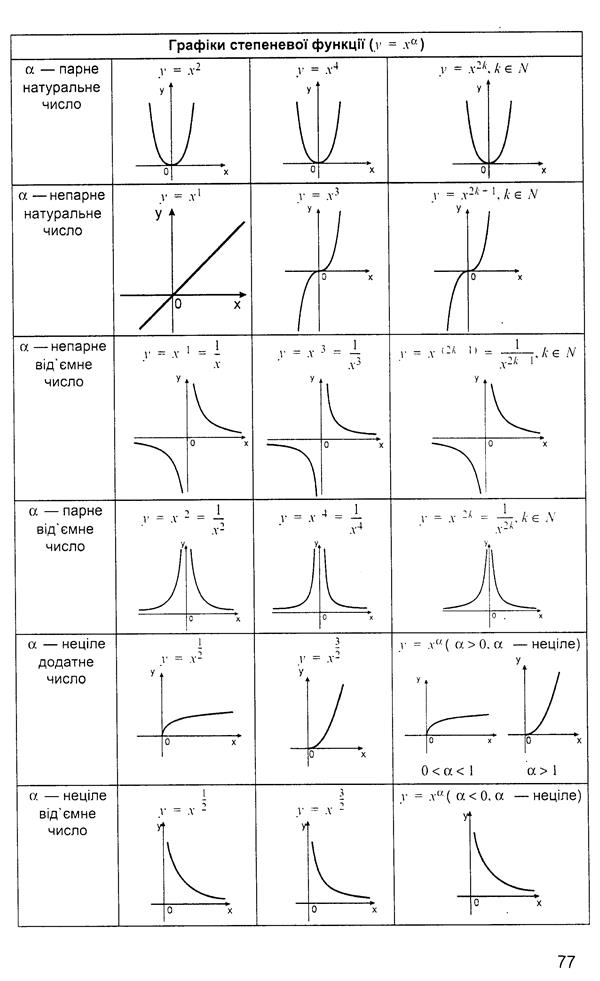
Означення: Логарифмом числа 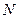 за основою
за основою 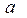 (
(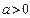 ,
, 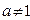 ) називається показник степеня
) називається показник степеня 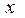 , до якого треба піднести
, до якого треба піднести 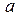 , щоб дістати число
, щоб дістати число  .
.
Те, що число 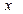 є логарифмом числа
є логарифмом числа 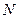 за основою
за основою 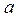 , записують так:
, записують так: 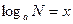
Вираз 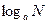 , де
, де 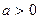 ,
, 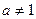 ,має смисл лише при
,має смисл лише при 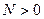
Логарифми за основою 10 називають десятковими логарифмами і позначають 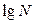 .
.
Основна логарифмічна тотожність

Для будь-якого 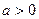
 і
і  виконуються рівності:
виконуються рівності:
1. 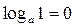 6.
6. 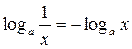
2. 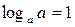 7.
7. 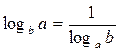 , або
, або 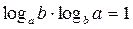
3. 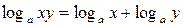 8.
8. 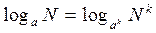
4. 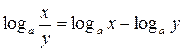 9.
9. 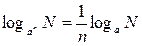
5. 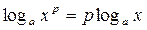 10.
10. 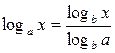
для будь-якого дійсного р. 11. 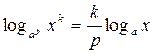
Логарифми з основою 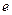 називають натуральними, або неперовими і позначають
називають натуральними, або неперовими і позначають 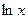 .
.
Означення: функцію задану формулою 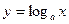 (1) називають логарифмічною функцією за основою а.
(1) називають логарифмічною функцією за основою а.
Перелічимо основні властивості логарифмічної функції.
1. Область визначення логарифмічної функції –множина всіх додатних чисел R+, тобто D(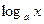 )= R+.
)= R+.
2. Область значень логарифмічної функції - множина всіх дійсних чисел.
3. Логарифмічна функція на всій області визначення зростає (якщо 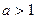 ) або спадає (якщо
) або спадає (якщо 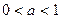 ).
).
Графіки показникової і логарифмічної функцій, що мають однакову основу, симетричні відносно прямої  .
.
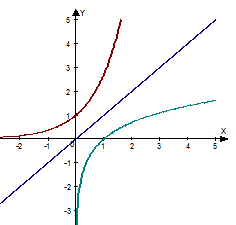
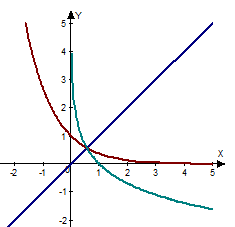

Логарифмічні рівняння
-
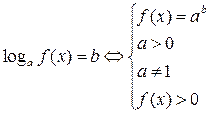
-
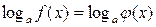
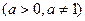
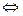
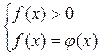 або
або 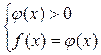
-
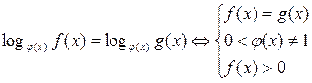
Логарифмічні нерівності
1. 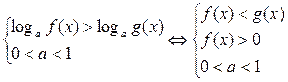 2.
2. 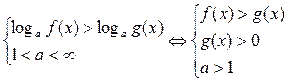
3. 
4. 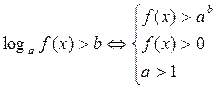 і
і 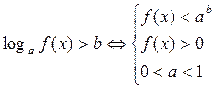
5. 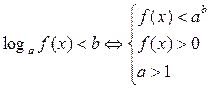 і
і 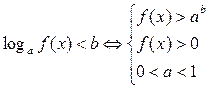
Властивості числових нерівностей:
1. 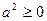
2. 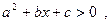 якщо
якщо 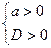
3. 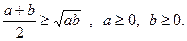
4. 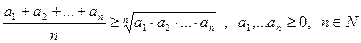 (нерівність Коші)
(нерівність Коші)
5. 
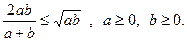
 - середнє арифметичне
- середнє арифметичне
6.  якщо
якщо 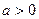 .
. 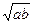 - середнє геометричне
- середнє геометричне
7. 
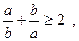 якщо
якщо 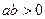 .
. 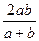 - середнє гармонічне
- середнє гармонічне
8. 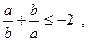 якщо
якщо 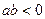 .
.
9. 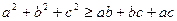 (нерівність трьох квадратів)
(нерівність трьох квадратів)
10. 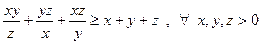 .
.
11. 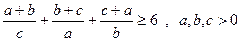 .
.
12. 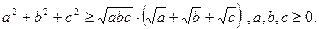
13. 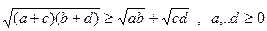 .
.
14. 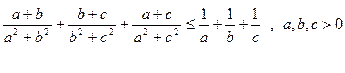
Нерівності з модулями і коренями:
1. 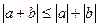
2. 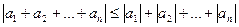
3. 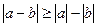
4. 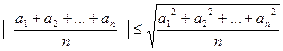
5. Якщо 
Визначні числові нерівності:
1. 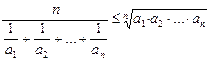 (середнє гармонічне додатних чисел не більше за середнє геометричне)
(середнє гармонічне додатних чисел не більше за середнє геометричне)
2.  (середнє арифметичне чисел не більше за середнє квадратичне)
(середнє арифметичне чисел не більше за середнє квадратичне)
Рівність в обох формулах досягається лише за умови, що 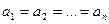
3. 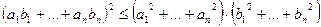 - нерівність Коші – Буняковського для
- нерівність Коші – Буняковського для 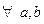 .
.
(нерівність має знак рівності, якщо  )
)
4. 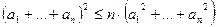 - (наслідок з нерівності Коші –Буняковського)
- (наслідок з нерівності Коші –Буняковського)
5. 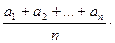
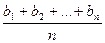

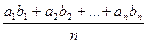 - нерівність Чебишева для
- нерівність Чебишева для  ,
, 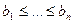
6. 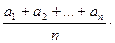
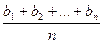
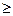
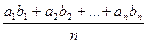 - нерівність Чебишева для
- нерівність Чебишева для  ,
, 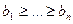 .
.
7. 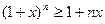 - нерівність Бернуллі для
- нерівність Бернуллі для 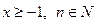
8. 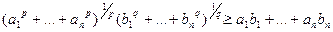 - нерівність Гельдера (справджується для додатних
- нерівність Гельдера (справджується для додатних 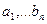 , раціональних
, раціональних 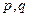 , причому
, причому 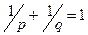 .
.
9. Нерівність Мінковського.

(знак нерівності потрібно змінити на протилежний, якщо 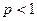 )
)
Таблиця похідних деяких функцій
| Елементарні функції | Складені функції | Правила диференціювання |
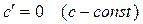
| 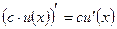 Сталий множник можна виносити за знак похідної
Сталий множник можна виносити за знак похідної
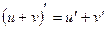 Похідна суми функцій, що диференціюються, дорівнює сумі їхніх похідних
Похідна добутку
Похідна суми функцій, що диференціюються, дорівнює сумі їхніх похідних
Похідна добутку
 Похідна частки
Похідна частки

| |
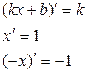
| ||
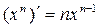
| 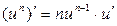
| |
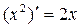
| 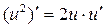
| |
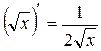
| 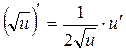
| |
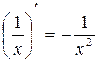
| 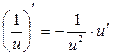
| |
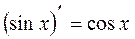
| 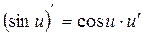
| |
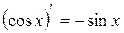
| 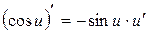
| |
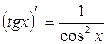
| 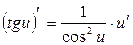
| |
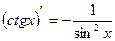
| 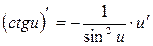
| |
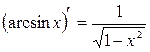
| 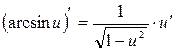
| |
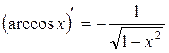
| 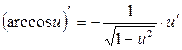
| |
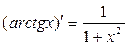
| 
| |

| 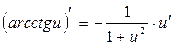
| |
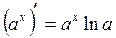
| 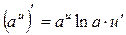
| |
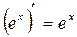
| 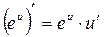
| |
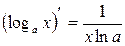
| 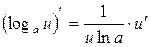
| |
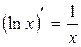
| 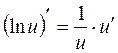
|
Застосування похідної
Механічний зміст похідної: якщо матеріальна точка рухається прямолінійно за законом S=S (t), то швидкість її руху v(t) в момент часу t дорівнює похідній s¢(t):
v(t) = S¢(t).
Зауваження: прискорення руху матеріальної точки а(t) в момент часу t дорівнює похідній v¢(t):
a(t) = v¢(t) = S¢¢(t).
 Геометричний зміст похідної: Значення похідної функції
Геометричний зміст похідної: Значення похідної функції 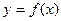 в точці
в точці 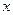
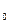 дорівнює кутовому коефіцієнту дотичної до графіка функції в точці з абсцисою x
дорівнює кутовому коефіцієнту дотичної до графіка функції в точці з абсцисою x 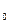 :
:

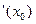 = k =
= k = 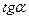
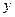 y=kx+b
y=kx+b
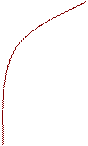 y=f(x)
y=f(x)



 y0
y0
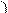 a
a
 0 x0
0 x0 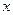
Рівняння дотичної до графіка функції 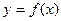 в точці з абсцисою
в точці з абсцисою 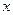
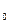 має вигляд:
має вигляд:
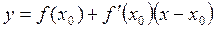
Дві прямі 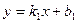 і
і 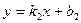 паралельні тоді і тільки тоді, коли
паралельні тоді і тільки тоді, коли 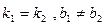 .
.
Дві прямі 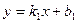 і
і 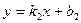 перпендикулярні тоді і тільки тоді, коли
перпендикулярні тоді і тільки тоді, коли 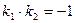 .
.
Кутом між графіками функцій 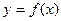 і
і 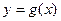 у точці їх перетину називається кут між дотичними до їх графіків у цій точці.
у точці їх перетину називається кут між дотичними до їх графіків у цій точці.
Величина кута 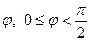 між двома прямими
між двома прямими 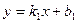 і
і 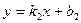 визначається із співвідношення:
визначається із співвідношення: 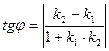
Т! (достатня ознака зростання (спадання) функції).
· Якщо  > 0 на інтервалі
> 0 на інтервалі 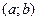 , то функція
, то функція 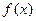 монотонно зростає на цьому інтервалі;
монотонно зростає на цьому інтервалі;
· Якщо  < 0 на інтервалі
< 0 на інтервалі 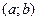 , то функція
, то функція 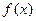 монотонно спадає на цьому інтервалі.
монотонно спадає на цьому інтервалі.
“ Алгоритм дослідження функції на монотонність”
1. знайти область визначення функції і точки розриву;
2. Знайти похідну функції;
3. записати і розв’язати нерівність  > 0 і вибрати з множини її розв’язків проміжки, де функція визначена. Знайдені проміжки є проміжками зростання функції;
> 0 і вибрати з множини її розв’язків проміжки, де функція визначена. Знайдені проміжки є проміжками зростання функції;
4. записати і розв’язати нерівність  < 0 і вибрати з множини її розв’язків проміжки, де функція визначена. Знайдені проміжки є проміжками спадання функції.
< 0 і вибрати з множини її розв’язків проміжки, де функція визначена. Знайдені проміжки є проміжками спадання функції.
Date: 2015-08-15; view: 532; Нарушение авторских прав