Примечания. 1. См. рисунки 56 и 57 в книге Rawson and Legeza, Tao (1979), где линии дракона изображены как вихри в облаках

1. См. рисунки 56 и 57 в книге Rawson and Legeza, Tao (1979), где линии дракона изображены как вихри в облаках, энергии, которые можно обуздать.

2. См., например, стр. 125 в книге Питера Саттона «Сновидения: искусство аборигенов Австралии» (Peter Sutton, Dreamings: The art of Aboriginal Australia (1988), «Witchedy Grub Dreamings»).

3. С рисунка 150 в упомянутой книге Саттона

4. В главе 26 мы обсуждали детали пространственно-временного интервала – расстояния, измеряемого в четырехмерной Вселенной, которое можно записать для четырех главных измерений пространства-времени как:

s2 = x 12 + x 22 + x 32 + x 42

или для трех пространственных координат x, y и z и временной координаты t как:

s2 = х2 + y2 + z2 + (-ict)2.

Для простоты мы можем пока рассматривать только движения в направлении х. Тогда нам больше не нужно вводить в уравнение измерения y и z, и в упрощенном виде выражение для пространства-времени будет выглядеть так:

s2 = x 12 + x 42.

Но поскольку четвертое измерение – это ict, мы окончательно получаем следующее упрощенное уравнение для пространственно-временного интервала:

s 2 = x 2 – (ct)2.

Иными словами, следствие мнимых чисел в пространстве времени состоит в появлении знака минус перед временным измерением. Более того, иногда сам пространственно-временной интервал становится мнимым. Если подставить в приведенную выше формулу реальные значения для х и ct – скажем, x = 1 и ct = 2, то получится:

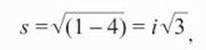
поскольку квадратный корень из отрицательного числа – это мнимое число. Если x больше ct, например, x = 2 и ct = 1, то получится действительное число – квадратный корень из (4 – 1) = 3, равный примерно 1,7.

5. Теория Хоукинга выражена восхитительно простым языком в книге физика Поля Дэвиса «О времени, незаконченная революция Эйнштейна» (Paul Davies, About Time, Einstein’s Unfinished Revolution (1995).

6. Если мы имеем дело с временным измерением в 1 минуту и пространственным различием, равным нулю, то s2 = x2 – (ct)2, x = 0, и s равно квадратному корню из отрицательного числа и, следовательно, является мнимым.

7. Если подставить для времени t мнимый временной множитель, то -ict превращается в ic х it, что равно + ct, поскольку i х i = -1.

8. Вы уже знакомы с нелинейным временем из главы 4, где я цитировал древний отрывок из И-Цзин, в котором говорится «Счет того, что идет вперед, идет назад». Это утверждение относится к опыту НОР движения вперед во времени ОР, делаясь старше, наблюдая, как проявляются вещи, развертываясь из чувственных семян и одновременно осознавая, что в НОР ты удаляешься от чувственных корней реальности.

По большому счету, время не такая уж полезная идея, поскольку оно не соотносится с ощущением в НОР событий, развертывающихся из данного корня. В терминах ОР переживание мнимого времени относится к выходу из линейного времени, способности фантазировать, воображать, сновидеть, двигаться назад или вперед во времени и из времени.

9. Здесь я использую термин «самоотражение» для выражения математической идеи, сформулированной в примечании 4, где замена времени t мнимым временем (it) позволяет делать вычисления в начале Вселенной:

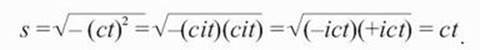
В начале Вселенной сомножители времени -cit и +cit конъюгируются или самоотражаются.

Date: 2015-08-15; view: 311; Нарушение авторских прав