Примечания. 1. Основная идея, на которой основывается вывод Эйнштейном преобразования Лоренца, состоит в том, что скорость света остается постоянной во всех системах

1. Основная идея, на которой основывается вывод Эйнштейном преобразования Лоренца, состоит в том, что скорость света остается постоянной во всех системах отчета и что расстояние равно произведению скорости на время. Вот примерный вывод. Расстояние, проходимое в одном измерении скорости света, равно х = ct, или х2 – c2t2 = 0. Видимость того же самого события в любой другой системе отсчета, назовем ее х' и t', должна означать, что х'2 – c2t'2 = 0. Если мы рассмотрим общий случай распространения света, которое происходит не строго по прямой линии и не обязательно должно быть Евклидовым или согласовываться с теоремой Пифагора, где гипотенуза равна квадратному корню из суммы квадратов сторон, тогда в трех измерениях и в общем случае

х12 + у12 + z12 – c2' = х12 + у2 = z12 – c2' = s2,

где s – пространственно-временной интервал.

Если мы вспомним, что х = vt и установим у = z = 0, то приведенное выше уравнение дает нам преобразование Лоренца для одного измерения, показанное на рис. 25.5 (Более подробно об этом выводе можно прочитать в книге Эйнштейна «Смысл относительности»).

В общем случае, получающееся преобразование Лоренца из одной системы в другую при наличии значений на земле х, e, t и z дает значения в системе, движущейся по отношению к земле со скоростью v, равные х', у', z', t' (когда у = у' и z = z1).

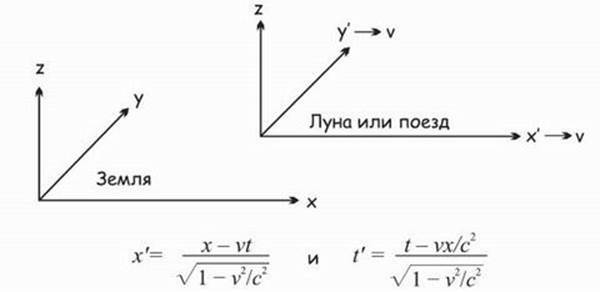
Рис. 25.5. Связь между пространствами и временами в относительных системах отсчета

Скорость поезда (или Луны) относительно земли равна

v = x/t.

Если мы берем линейку, отмеряющую 1 метр в движущейся системе, вроде поезда или Луны, видимых с земли, то получаем там X. Какую длину будет иметь этот метр для людей, измеряющих на земле? Поскольку

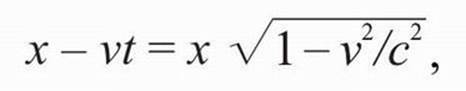
то при х' = 1 и t = 0

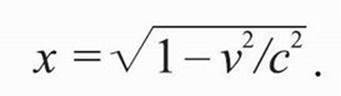
Это показывает, что для очень малых скоростей (скажем, поезда) х тоже примерно равно 1 метру. Но для очень больших скоростей, когда кто-то на поезде измеряет 1 метр, кто-то на земле будет думать, что линейка укоротилась! Вы можете видеть, что если v становится больше с, то

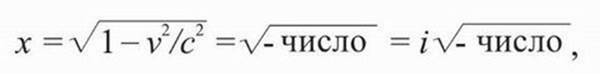
поскольку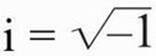

, и мы получаем мнимые величины. Таким образом, согласно сегодняшней физике, ничто не может двигаться быстрее скорости света, поскольку такое движение невозможно измерить в ОР. Все, превышающее скорость света, относится к мнимым мирам, к сновидению. Кроме того, из формулы для t на рис. 25.5 при х = 0 следует, что с возрастанием скоростей, время в 1 секунду, измеряемое на поезде, при измерении кем-то на земле будет меньшим 1 секунды; с увеличением v время сжимается, поскольку

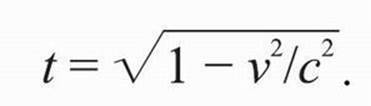
2. В Примечании 1 показано, как получаются мнимые числа, если v = x/t больше, чем с.

3. Прежде чем мы пойдем дальше и больше узнаем о пространстве-времени, давайте еще немного подумаем о нем. Это не будет сложно, но могло бы показаться сложным, если бы давно не имели дела с прямоугольными треугольниками. Я хочу немного поговорить о треугольниках и постараться показать, как учитель математики Эйнштейна Германн Минковски по-новому оценил и, в некоторых отношениях, упростил результаты Эйнштейна.

Минковски смотрел на s и понимал, что это нечто вроде диагонали или гипотенузы – длинной стороны прямоугольного треугольника.

Рис. 25.6. Формула Евклида для прямоугольных треугольников

Минковски смотрел на формулу для прямоугольных треугольников и думал ее сходстве с уравнением для пространства-времени:

s2 = x2 + y2 + z2 – c2t2.

Если для простоты заменить координаты x, у и z одной пространственной координатой, скажем x, то мы получим такое уравнение:

s2 = x2 – c2t2.

Эта формула пространства-времени похожа на формулу

с2 = a2 + b2

для прямоугольного треугольника, где с – это расстояние.

Минковски смотрел на это и думал: «Ммм, это s или пространство-время четырехмерно (три пространственных и одно временное измерение), в то время как тот плоский треугольник двумерен. Как насчет того, чтобы свести s к двум измерениям, поскольку его трудно представлять себе в четырех измерениях. В нашем повседневном трехмерном мире нет ничего похожего на четырехмерную реальность. Физики будущего захотят зрительно представлять себе работу Эйнштейна по теории относительности, но слишком странно, если невозможно зрительно представлять себе то, о чем он говорит».

Поскольку два или три измерения легче представлять, Минковски решил свести четырехмерное гиперпространство, состоящее из x, y, z и t, к двум измерениям. Он приближенно представлял его как плоский треугольник. Это похоже на приближенную оценку площади неровной поверхности части земли. Кривую поверхность трудно измерить, и потому вы приближенно оцениваете ее, считая ее плоской и используя формулу для вычисления площади как произведения длины на ширину.

Стараясь получить зрительное представление нового, четырехмерного мира, Минковски просто переименовал пространства и времена, чтобы иметь с ними дело на равных основаниях. Он обозначил пространственное измерение как x 1 (x = x 1), а временное измерение как x4 (-ict = x4) и получил более простую формулу, имевшую форму прямоугольного треугольника:

s2 = x 12 + x 42.

Цель всего этого заключалась в том, чтобы представить гиперпространство в терминах обычной реальности. И действительно, приведенная выше четырехмерная формула для пространства-времени выглядит как формула для диагонали прямоугольного треугольника! Если мы можем представить себе треугольник в двух измерениях, то s становится своего рода диагональю.

Математика Минковски достигает упрощения, скрывая мнимое измерение времени. Новый мир Минковски представляет собой сочетание пространственных измерений общепринятой реальности и временных измерений, но перед временем стоит мнимое число (так как -ict = x4)! Иными словами, очень трудно представить себе измерение времени!

Но мы уже знали с самого начала и без математики, что время обладает пространственными качествами, но движение во времени трудно себе представить. В своем мышлении мы рассматриваем время как пространство. (Например, если бы я спросил: «Как долго вам добираться по шоссе до следующего города?», – вы могли бы ответить: «Около 500 миль».)

Минковски дал измерению x новое название. Это все равно, что называть вас не вашим именем, а именем «пространство 1». Он дал x название x1! Он также переименовал у, назвав его «пространство 2», или x2. Точно так же z превратился в x3. «А что же делать со временем, – думал он, – перед которым стоит тот неудобный знак минус, а именно -c2t2»? Он решил, пусть временное измерение будет x4.

Это было действительно хитро, так как он спрятал знак минус в слагаемом (-c2t2), обозначив x42 = (-ict)2 и, следовательно, x4 = -ict, так как корень квадратный из минус единицы равен i. (Помните главу 7?) С новыми названиями пространство-время начинает выглядеть немного привычнее:

s2 = x12 + x22 + x32 + x42,

поскольку x = x1, y = x2, z = x3, и -ict = x4, что при y = z = 0 сводится к

s 2 = x 2 + x 2.

4. Но подождите, что же случилось со временем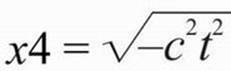

? Поскольку квадратный корень из отрицательного числа, вроде -1, равен i, теперь мы имеем x4 = ict.

5. Вычисление пространства-времени. Допустим, что вам не нужны у и z для измерения расстояния, которое планета проходит в одном пространственном измерении х. Тогда мы можем изобразить пространство-время в виде двухмерной карте, которую мы легко себе представляем. Теперь пространство-время представлено в двух измерениях.

Попробуем, например, измерить пространственно-временной интервал планеты, которая прошла 250 миль в пространстве и 1 год по местному времени.

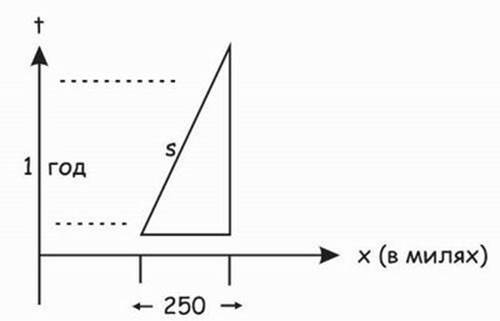
Рис. 25.7. Пространственно-временной график измерения 250 миль и 1 года

Теперь мы могли бы подставить эти величины в приводившиеся выше формулы для х и t и получить s – пространственно-временной интервал, который планета прошла за 1 год земного времени и 250 миль земного пространства. Точно так же мы могли бы даже измерить скорость движения планеты во времени!Смысл нахождения пространственно-временного интервала состоит в том, что эта величина s не зависит от точки зрения, с которой вы ее измеряете.Если бы планета оставалась неподвижной в пространстве, она бы все равно двигалась во времени – в конце концов, она ведь становится старше!

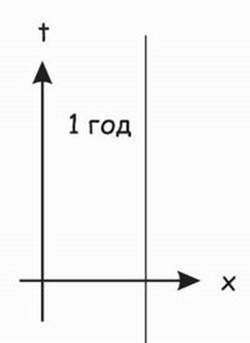
Рис. 25.8. Движение в пространстве-времени, когда нет движения в пространстве

При движении только во времени планета движется в пространстве-времени по прямой линии, поскольку x, у и z вообще не меняются. Существует ли скорость движения во времени? Безусловно, существует. В этом случае скорость движения во времени c = s/t. Как может быть скорость движения вещей во времени? Эта скорость – скорость света. Поэтому, даже не перемещаясь ни на сантиметр с точки зрения данной системы отсчета, вы движетесь сквозь время со скоростью света.

Человек на Луне измеряет x1' и х4'. Поскольку

s2 = х12 + х42 = х' + x/2.

В графическом виде это уравнение показано на рис. 25.9.

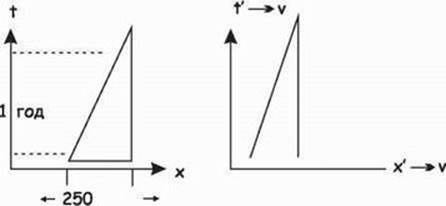
Рис. 25.9 Относительные измерения, видимые на Земле и в движущейся системе

Я измеряю 250 миль и мое время t равно 1 году, однако для человека на поезде, движущемся относительно Земли, х' и t' будут другими.

6. В математике теории относительности пространство-время связано с мнимым временем. См. примечание 3, где временные факторы для всякого наблюдателя определяются как время, измеряемое в его системе отсчета, умноженное на скорость света и на мнимое число, то есть ict. Я очень признателен своему другу Джо Гудбреду за интересные обсуждения связи пространства-времени и относительности.

Date: 2015-08-15; view: 393; Нарушение авторских прав