Вопрос 29

Случайной величиной называется измеряемая по ходу опыта

численная характеристика, принимающая одно и только одно возможное и наперёд неизвестное значение вследствие действия различных факторов, которые не могут быть заранее учтены.

Функцией распределения случайной величины называетсяфункция, определяемая равенством F(x) = P(X ≤ x)

Функция f(x) называется плотностью вероятности непрерыв-

ной случайной величины, если для любых чисел a и b (b > a) выпол-

няется равенство

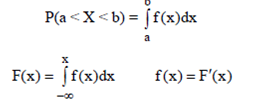
Распределения вероятностей случайных величин могут быть дискретными и непрерывными.

Наиболее важным непрерывным распределением вероятностей, используемых в аналитической химии, является нормальное распределение.

Выборкой называется последовательность независимых одинаково распределённых случайных величин. Выборка, пронумерованная в порядке возрастания, т.е. x1, x2... xn, называется вариационным рядом. Сами значения x называются вариантами.

Выборочное среднее - сумма всех значений серии наблюдений, делённая на число наблюдений.

Выборочная дисперсия - сумма квадратов отклонений, делённая на число степеней свободы. Число степеней свободы f = n-1 – число переменных, которые могут быть при-

своены произвольно при характеристике данной выборки.

выборочное стандартное отклонение - положительный квадратный корень из

выборочной дисперсии.

Для характеристики выборок малых объёмов (n <30), взятых из нормально распределённых генеральных совокупностей, используют распределение Стьюдента (t-распределение), представляющее собой распределение случайной величины t

Доверительным интервалом называется интервал, вероятность попадания значений случайной величины в который равна принятой нами доверительной вероят-

ности 1-α, где α - уровень значимости (в аналитической практике α =0,05).

Процесс анализа многостадиен.Перед началом статистической обработки необходимо проверить, не содержат ли полученные результаты грубых погрешностей.

Измерения, в которых обнаружены такие погрешности, должны быть

исключены. Для исключения промахов при работе с выборками малого объёма (n = 4 - 10) можно воспользоваться величиной Q-критерия.

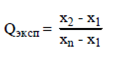
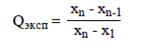
Полученное значение сравнивают с критической (табличной) величиной для Q-критерия. Если оно превышает последнюю, то проверяемый результат является промахом и его необходимо исключить из дальнейших расчётов.

Преобразуем выборку, приведенную в примере в вариационный ряд. Дальше находим выборочное среднее, выборочную дисперсию, выбороч стандарт отклонение, страндарт отклонение от выборочного среднего, относительное стандартное отклонение.

Значащие цифры -все достоверные цифры, входящие в состав численной величины, а также первую следующую за ними недостоверную цифру. 103,2- первые три цифры(1,0 и 3) известны точно, последняя(2) имеет недостоверность, след. 103,2+-0,1.

Положение запятой не влияет на кол-во значащих цифр. Нули в составе числа могут быть как значимыми, так и незначимыми.

Принцип округления: если первая цифра, следующая за округляемой, меньше 5, то округляемая цифра не изменяется, если больше 5, то округляемая цифра увеличивается на 1. Если цифра после округляемой точно равна 5, то четную округляемую цифру оставляют без изменений, а нечетную увеличивают на 1.

Date: 2015-08-15; view: 584; Нарушение авторских прав