Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Определение формулы логики предикатов (по индукции)
|
|
1) Каждая нульместная предикатная переменная есть формула.
2) Если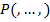 
- n-местная предикатная переменная, то 
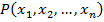– формула, в которой все предметные переменные 
свободны.
3) Если F – формула, то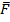 
- тоже формула. Свободные (связанные) предметные переменные в формуле 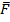те и только те, которые являются свободными (связанными) в F.
Характер предметных переменных при переходе от формулы F к 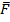не меняется.
4) Если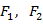 
- формулы, и если предметные переменные, входящие одновременно в эти формулы, свободны в любых из них, то выражения
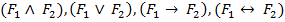также являются формулами.
5) Если F – доказуемая формула и x – предметная переменная, входящая в F свободно, то выражения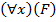 
и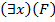 
также являются формулами, в которых переменная x связанная, а все остальные переменные – предметные, входящие в формулу F свободно или связанно, остаются и в новых формулах такими же соответственно.
6) Никаких других формул логики предикатов нет.
Определение. Формулы, определенные в пунктах 1-2, называются элементарными (атомарными). Формулы, не являющиеся элементарными, называются составными.
Пример.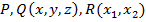 
- элементарные формулы.
На основании пунктов 1, 3, 4 всякая формула алгебры высказываний будет также и формулой логики предикатов.
Определение. Формулы, в которых нет свободных предметных переменных, называются замкнутыми. Формулы, содержащие свободные предметные переменные – открытыми.
Примеры замкнутых формул: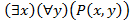 
,
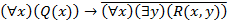
§ 9. Классификация формул логики предикатов
Если в формуле логики предикатов вместо каждой предикатной переменной подставить конкретный предикат, определенный на некотором выбранном множестве M, то формула превратится в конкретный предикат, заданный над множеством M. При этом, если исходная формула была замкнутой, то полученный конкретный предикат окажется нульместным, то есть будет высказыванием. Если же исходная формула была открытой, то есть содержала свободные вхождения предметных переменных, то в результате подстановки получим предикат, зависящий от некоторых предметных переменных. Если теперь вместо этих предметных переменных подставить конкретные предметы из множества M, то полученный предикат, а в конечном итоге – исходная формула, превратится в высказывание.
Получаемое высказывание, а также процесс превращения формулы логики предикатов в высказывание описанным способом, называется интерпретацией этой формулы на множестве M.
Пример. Дадим интерпретацию формуле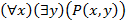 
.
В качестве множества M возьмем множество всех мужчин, а вместо предикатной переменной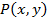 
подставим конкретный предикат, определенный на M: «x есть брат y». Тогда исходная формула превратится в следующее высказывание
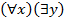(«x есть брат y») –«у каждого мужчины есть брат». Высказывание, очевидно, ложное.
Date: 2015-08-15; view: 814; Нарушение авторских прав