Обратная матрица и алгоритм ее нахождения

Понятие обратной матрицы вводится только для квадратных матриц.

Если A – квадратная матрица, то обратной для неё матрицей называется матрица, обозначаемая A^-1 и удовлетворяющая условию 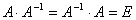. Справедлива следующая теорема:

Для того чтобы квадратная матрица A имела обратную, необходимо и достаточно, чтобы её определитель был отличен от нуля.

Доказательство: Необходимость. Пусть для матрицы A существует обратная матрица A^-1. Покажем, что | A | ≠ 0. Прежде всего заметим, что можно доказать следующее свойство определителей .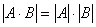

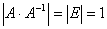Предположим, что | A | = 0. Тогда . Но с другой стороны . Полученное противоречие и доказывает, что | A | ≠ 0.

Достаточность. Для простоты доказательство проведём для случая матрицы третьего порядка.

Пусть и | A | ≠ 0.

Покажем, что в этом случае обратной матрицей будет матрица , где A_ij алгебраическое дополнение элемента a_ij.

Найдём AB=C.

Заметим, что все диагональные элементы матрицы C будут равны 1. Действительно, например,

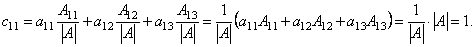
Аналогично по теореме о разложении определителя по элементам строки можно доказать, что c₂₂ = c₃₃ = 1.

Кроме того, все недиагональные элементы матрицы C равны нулю. Например,

Следовательно, AB=E. Аналогично можно показать, что BA=E. Поэтому B = A^-1.

Таким образом, теорема содержит способ нахождения обратной матрицы.

Если условия теоремы выполнены, то матрица обратная к матрице находится следующим образом

,

где A_ij - алгебраические дополнения элементов a_ij данной матрицы A.

Итак, чтобы найти обратную матрицу нужно: 1.Найти определитель матрицы A. 2.Найти алгебраические дополнения A_ij всех элементов матрицы A и составить матрицу , элементами которой являются числа A_ij.

3.Найти матрицу, транспонированную полученной матрице , и умножить её на – это и будет .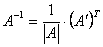

Аналогично для матриц второго порядка, обратной будет следующая матрица .

Date: 2015-08-15; view: 527; Нарушение авторских прав