
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Задачи для самостоятельного решения. 1. Написать уравнение гармонического колебательного движения с амплитудой в 5 см, если в 1 мин совершается 150 колебаний и начальная фаза колебаний равна
|
|
1. Написать уравнение гармонического колебательного движения с амплитудой в 5 см, если в 1 мин совершается 150 колебаний и начальная фаза колебаний равна 45°.
2. Определить максимальные значения скорости vmax и ускорения a max точки, совершающей гармонические колебания с амплитудой А=3 см и циклической частотой ω=π/2 рад/с.
3. Точка совершает гармонические колебания. Наибольшее смещение точки равно 10 см, наибольшая скорость 20 см/с. Найти циклическую частоту колебаний и максимальное ускорение точки.
4. Точка совершает колебания по закону x=A sinωt. В некоторый момент времени смещение точки х1 оказалось равным 5 см. Когда фаза колебаний увеличилась вдвое, смещение х2 стало равным 8 см. Найти амплитуду А колебаний.
5. Написать уравнение движения, получающегося в результате сложения двух одинаково направленных гармонических колебательных движений с одинаковым периодом 8 с и одинаковой амплитудой 0,02 м. Разность фаз между этими колебаниями равна π/4. Начальная фаза одного из колебаний равна нулю.
6. Найти амплитуду и начальную гармонического колебания, полученного от сложения одинаково направленных колебаний, данных уравнениями х1 =0,02sin(5πt+π/2) м и х2 =0,03sin(5πt+π/4) м.
7. Материальная точка массой 50 г совершает колебания, уравнение которых имеет вид x=A cosωt, где А=10 см, ω=5 рад/с. Найти силу, действующую на точку в двух случаях: 1) в момент, когда фаза ωt=π/3 рад; 2) в положении наибольшего смещения точки.
8. Точка участвует в двух колебаниях одинакового периода с одинаковыми начальными фазами. Амплитуда колебаний А1=3 см и А2=4 см. Найти амплитуду результирующего колебания, если: 1) колебания совершаются в одном направлении, 2) колебания взаимно-перпендикулярны.
9. Точка участвует одновременно в двух взаимно-перпендикулярных колебаниях x=2 sinωt м и у=2 соsωt м. Найти траекторию движения точки.
10. Точка участвует одновременно в двух взаимно-перпендикулярных колебаниях x=sinπt м и у = 2 sin(πt+π/2) м. Найти траекторию движения точки и вычертить ее с нанесением масштаба.
11. Точка участвует одновременно в двух взаимно-перпендикулярных колебаниях x=sinπt м и у = 4 sin(πt+π) м. Найти траекторию движения точки и вычертить ее с нанесением масштаба.
12. Сложите графически два гармонических, одинаково направленных колебания равных периодов, но смещенных по фазе друг относительно друга на π. Амплитуды относятся между собой как 3:1.
13. Складываются два гармонических колебания одного направления с одинаковыми периодами 1,5 с и амплитудами по 2 см. Начальные фазы колебаний φ1=π/2 рад и φ2=π/3 рад. Определить амплитуду и начальную фазу результирующего колебания. Найти его уравнение и построить с соблюдением масштаба векторную диаграмму сложения амплитуд.
14. Складываются три гармонических колебания одного направления с одинаковыми периодами 2 с и амплитудами по 3 см. Начальные фазы колебаний φ1=0, φ2=π/3 рад и φ3=2π/3 рад. Построить векторную диаграмму сложения амплитуд. Определить из чертежа амплитуду и начальную фазу результирующего колебания.
15. Определить массу тела, совершающего гармонические колебания с амплитудой 0,1 м, частотой 2 Гц и начальной фазой 30°, если полная энергия колебаний 7,7 мДж. Через сколько секунд от начала отсчета времени кинетическая энергия будет равна потенциальной?
16. Грузик массой 250 г, подвешенный к пружине, колеблется по вертикали с периодом Т=1 с. Определить жесткость пружины.
17. Гиря, подвешенная к пружине, колеблется по вертикали с амплитудой 4 см. Определить полную энергию колебаний гири, если жесткость пружины равна 1 кН/м.
18. Тонкий обруч, подвешенный на гвоздь, вбитый горизонтально в стену, колеблется в плоскости, параллельной стене. Радиус обруча равен 30 см. Вычислить период колебаний обруча.
19. Найти возвращающую силу в момент t = 1 с и полную энергию материальной точки, совершающей колебания по закону x=A cos ωt, где А=20 см, ω=2π/3 рад/с. Масса материальной точки равна 10 г.
20. Определить массу тела, совершающего гармонические колебания с амплитудой 0,1 м, частотой 2 Гц и начальной фазой 30°, если полная энергия колебаний 7,7 мДж. Через сколько секунд от начала отсчета времени кинетическая энергия будет равна потенциальной?
21. Однородный стержень совершает малые колебания в вертикальной плоскости около горизонтальной оси, проходящей через его верхний конец. Длина стержня 0,5 м. Найти период колебаний стержня.
22. Найти период колебаний стержня предыдущей задачи, если ось вращения проходит через точку, находящуюся на расстоянии 10 см от его верхнего конца.
23. Однородный шарик подвешен на нити, длина которой равна радиусу шарика. Во сколько раз период малых колебаний этого маятника больше периода малых колебаний математического маятника с таким же расстоянием от точки подвеса до центра тяжести?
24. Период колебаний крутильного маятника, состоящего из кольца, соединенного спиральной пружиной с осью вращения, равен Т=4с. Определить момент инерции, если жесткость пружины k=10-2 Нм. Трением пренебречь.
25. Математический маятник длиной 40 см и физический маятник в виде тонкого прямого стержня длиной 60 см синхронно колеблются около одной и той же горизонтальной оси. Определить расстояние центра масс стержня от оси колебаний.
26. Ареометр массой m=50 г, имеющий трубку диаметром d=1 см, плавает в воде. Ареометр немного погрузили в воду и затем предоставили самому себе, в результате чего он стал совершать гармонические колебания. Найти период T этих колебаний.
27. Амплитуда затухающих колебаний маятника за время t1=5 мин уменьшилась в два раза. За какое время t2, считая от начального момента, амплитуда уменьшится в восемь раз?
28. Амплитуда колебаний маятника длиной 1 м за время 10 мин уменьшилась в два раза. Определить логарифмический декремент колебаний.
29. За время 8 мин амплитуда затухающих колебаний маятника уменьшилась в три раза. Определить коэффициент затухания.
30. Логарифмический декремент колебаний маятника равен 0,003. Определить число полных колебаний, которые должен сделать маятник, чтобы амплитуда уменьшилась в два раза.
31. Найти частоту колебаний груза массой m=0,2 кг, подвешенного на пружине и помещенного в масло, если коэффициент трения в масле r=0,5 кг/с, а жесткость пружины k=50 Н/м.
В следующих задачах требуется найти уравнение движения груза D массы mD или системы грузов D и E массами mD и mE, отнеся движение к оси x. Начало неподвижной системы координат следует выбирать в положении статического равновесия груза или системы грузов. Грузы считать материальными точками. Весом пружин, жестких брусков, соединительных стержней и демпферов (устройств для создания сил вязкого сопротивления) пренебречь. Направление начальной скорости v0 совпадает с положительным направлением оси x. Значение величины  задается преподавателем.
задается преподавателем.
Задача 1. Груз D присоединен к системе трех пружин (рис.28) жесткостью  посредством бруска AB. Точка F подвеса груза выбрана из условия, что брусок движется поступательно, т.е.
посредством бруска AB. Точка F подвеса груза выбрана из условия, что брусок движется поступательно, т.е.  где
где  – жесткость пружины, эквивалентной последовательно соединенным пружинам жесткостью соответственно
– жесткость пружины, эквивалентной последовательно соединенным пружинам жесткостью соответственно  и
и  . В некоторый момент времени к покоящемуся грузу D подвешивают груз E и сообщают системе грузов D и E начальную скорость
. В некоторый момент времени к покоящемуся грузу D подвешивают груз E и сообщают системе грузов D и E начальную скорость  . Сопротивление движению двух грузов пропорционально их скорости v,
. Сопротивление движению двух грузов пропорционально их скорости v, 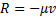 , где
, где  – коэффициент сопротивления.
– коэффициент сопротивления.
| mD, кг | mE, кг | v0, см/с | c 1, Н/см | c 2, Н/см | c 3, Н/см |  ,
кг/с ,
кг/с
|  ,
см ,
см
| p , 1/ с |
| – | – |

Рис.28
Задача 2. К пружине жесткостью 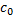 присоединен брусок AB (рис.29), к которому присоединены параллельные пружины жесткостью соответственно
присоединен брусок AB (рис.29), к которому присоединены параллельные пружины жесткостью соответственно  и
и  , в свою очередь, соединенные с бруском A1B1. К бруску A1B1 подвешены покоящиеся грузы D и E. Точка подвеса грузов и точка F подвеса бруска АВ выбраны так, что бруски движутся поступательно, т.е.
, в свою очередь, соединенные с бруском A1B1. К бруску A1B1 подвешены покоящиеся грузы D и E. Точка подвеса грузов и точка F подвеса бруска АВ выбраны так, что бруски движутся поступательно, т.е.  . В некоторый момент времени стержень, соединяющий грузы, перерезают и сообщают грузу D начальную скорость
. В некоторый момент времени стержень, соединяющий грузы, перерезают и сообщают грузу D начальную скорость  .
.
| mD, кг | mE, кг | v0, см/с | c 1, Н/см | c 2, Н/см | c 3, Н/см |  ,
кг/с ,
кг/с
|  ,
см ,
см
| p , 1/ с |
| 0.8 | – | – | – |
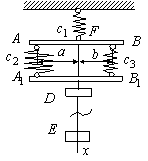
Рис.29
Задача 3. Покоящиеся грузы D и E присоединены к системе трех пружин (рис.30) жесткостью соответственно  посредством бруска AB. Точка F подвеса грузов выбрана из условия, что брусок движется поступательно, т.е.
посредством бруска AB. Точка F подвеса грузов выбрана из условия, что брусок движется поступательно, т.е.  , где
, где  – жесткость пружины, эквивалентной последовательно соединенным пружинам жесткостью
– жесткость пружины, эквивалентной последовательно соединенным пружинам жесткостью 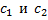 . В некоторый момент времени стержень, соединяющий грузы, перерезают и сообщают грузу D начальную скорость
. В некоторый момент времени стержень, соединяющий грузы, перерезают и сообщают грузу D начальную скорость  . Сопротивление движению груза D пропорционально его скорости v,
. Сопротивление движению груза D пропорционально его скорости v, 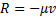 , где
, где  – коэффициент сопротивления.
– коэффициент сопротивления.
| mD, кг | mE, кг | v0, см/с | c 1, Н/см | c 2, Н/см | c 3, Н/см |  ,
кг/с ,
кг/с
|  ,
см ,
см
| p , 1/ с |
| 0.5 | – | – |

Рис.30
Задача 4. Покоящиеся грузы D и E присоединены к пружине (рис.31) жесткостью  , которая соединена с параллельными пружинами жесткостью
, которая соединена с параллельными пружинами жесткостью  и
и  посредством бруска AB. Точка подвеса F пружины 3 выбрана так, чтобы брусок AB двигался поступательно, т.е.
посредством бруска AB. Точка подвеса F пружины 3 выбрана так, чтобы брусок AB двигался поступательно, т.е.  . В некоторый момент времени стержень, соединяющий грузы, перерезают и сообщают грузу D начальную скорость
. В некоторый момент времени стержень, соединяющий грузы, перерезают и сообщают грузу D начальную скорость  . Сила сопротивления движению груза D пропорциональна его скорости v,
. Сила сопротивления движению груза D пропорциональна его скорости v, 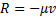 , где
, где  – коэффициент сопротивления.
– коэффициент сопротивления.
| mD, кг | mE, кг | v0, см/с | c 1, Н/см | c 2, Н/см | c 3, Н/см |  ,
кг/с ,
кг/с
|  ,
см ,
см
| p , 1/ с |
| 1.6 | – | – |
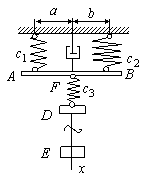
Рис.31
Задача 5. В некоторый момент времени груз E снимают с груза D (рис.32), когда оба груза находились в покое, и сообщают грузу D начальную скорость  . Брусок AB, к которому прикреплен груз D, соединен с параллельными пружинами жесткостью соответственно
. Брусок AB, к которому прикреплен груз D, соединен с параллельными пружинами жесткостью соответственно  и
и  , присоединенными к неподвижной тележке. Положение грузов D и E выбрано так, что брусок движется поступательно, т.е.
, присоединенными к неподвижной тележке. Положение грузов D и E выбрано так, что брусок движется поступательно, т.е.  . Сила сопротивления движению груза D пропорциональна его скорости v,
. Сила сопротивления движению груза D пропорциональна его скорости v, 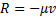 , где
, где  – коэффициент сопротивления.
– коэффициент сопротивления.
| mD, кг | mE, кг | v0, см/с | c 1, Н/см | c 2, Н/см | c 3, Н/см |  ,
кг/с ,
кг/с
|  ,
см ,
см
| p , 1/ с |
| – | – | – |

Рис.32
Задача 6. В некоторый момент времени груз E снимают с груза D (рис.33), когда оба груза находились в покое, и сообщают грузу D начальную скорость v0. Груз D соединен с пружиной жесткостью  , которая, в свою очередь, присоединена к бруску AB. Последний другой стороной соединен с параллельными пружинами жесткостью
, которая, в свою очередь, присоединена к бруску AB. Последний другой стороной соединен с параллельными пружинами жесткостью  и
и  , прикрепленными к неподвижной тележке. Точка F соединения пружины с бруском выбрана из условия, что брусок AB движется поступательно, т.е.
, прикрепленными к неподвижной тележке. Точка F соединения пружины с бруском выбрана из условия, что брусок AB движется поступательно, т.е.  .
.
| mD, кг | mE, кг | v0, см/с | c 1, Н/см | c 2, Н/см | c 3, Н/см |  ,
кг/с ,
кг/с
|  ,
см ,
см
| p , 1/ с |
| – | – | – |

Рис.33
Задача 7. В некоторый момент времени (t=0) груз E снимают с груза D (рис.34), когда оба груза находились в покое, и сообщают грузу D начальную скорость  . Груз D прикреплен к пружине жесткостью
. Груз D прикреплен к пружине жесткостью  , которая, в свою очередь, соединена с бруском AB. Последний соединен с параллельными пружинами жесткостью
, которая, в свою очередь, соединена с бруском AB. Последний соединен с параллельными пружинами жесткостью  и
и  нижние концы которых прикреплены к фундаменту, начинающему в этот же момент времени совершать вертикальное движение по закону
нижние концы которых прикреплены к фундаменту, начинающему в этот же момент времени совершать вертикальное движение по закону  . Точка F соединения пружины с бруском выбрана из условия, что брусок движется поступательно, т.е. a/b = c 3/ c 2.
. Точка F соединения пружины с бруском выбрана из условия, что брусок движется поступательно, т.е. a/b = c 3/ c 2.
Примечание. Положение начала отсчета на оси  соответствует среднему положению фундамента (
соответствует среднему положению фундамента (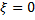 ).
).
| mD, кг | mE, кг | v0, см/с | c 1, Н/см | c 2, Н/см | c 3, Н/см |  ,
кг/с ,
кг/с
|  ,
см ,
см
| p , 1/ с |
| 1.5 | – |

Рис.34
Задача 8. В некоторый момент времени (t=0) груз E устанавливают на покоящийся груз D (рис.35) и сообщают системе грузов D и E начальную скорость  . Груз D присоединен к системе последовательно соединенных пружин жесткостью
. Груз D присоединен к системе последовательно соединенных пружин жесткостью  и
и  . В этот же момент времени нижний конец пружины (точка B) начинает совершать движение по закону
. В этот же момент времени нижний конец пружины (точка B) начинает совершать движение по закону  .
.
Примечание. Положение начала отсчета на оси x соответствует среднему положению точки В (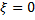 ).
).
| mD, кг | mE, кг | v0, см/с | c 1, Н/см | c 2, Н/см | c 3, Н/см |  ,
кг/с ,
кг/с
|  ,
см ,
см
| p , 1/ с |
| 1.2 | 4.8 | – | – |

Рис.35
Задача 9. В некоторый момент времени, когда грузы находились в покое, груз E снимают с груза D (рис.36) и сообщают грузу D начальную скорость  . Груз D присоединен к системе пружин жесткостью
. Груз D присоединен к системе пружин жесткостью  и
и  . Нижний конец нижней пружины прикреплен к неподвижной тележке.
. Нижний конец нижней пружины прикреплен к неподвижной тележке.
| mD, кг | mE, кг | v0, см/с | c 1, Н/см | c 2, Н/см | c 3, Н/см |  ,
кг/с ,
кг/с
|  ,
см ,
см
| p , 1/ с |
| 1.5 | – | – | – | – |

Рис.36
Задача 10. Покоящийся груз D соединен с бруском AB, связывающим параллельные пружины (рис.37) жесткостью  и
и  , которые присоединены к стене. Точка F соединения груза с бруском выбрана из условия, что брусок движется поступательно, т.е.
, которые присоединены к стене. Точка F соединения груза с бруском выбрана из условия, что брусок движется поступательно, т.е.  . В некоторый момент времени груз D отклоняют на величину
. В некоторый момент времени груз D отклоняют на величину  вправо и сообщают ему начальную скорость
вправо и сообщают ему начальную скорость  . Сила сопротивления движению груза D пропорциональна его скорости v,
. Сила сопротивления движению груза D пропорциональна его скорости v, 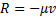 , где
, где  – коэффициент сопротивления.
– коэффициент сопротивления.
| mD, кг | mE, кг | v0, см/с | c 1, Н/см | c 2, Н/см | c 3, Н/см |  ,
кг/с ,
кг/с
|  ,
см ,
см
| p , 1/ с |
| 2.4 | – | – | – | – |

Рис.37
Задача 11. Покоящийся груз D присоединен к бруску AB (рис.38), который, в свою очередь, связан параллельными пружинами жесткостью  и
и  с бруском A1B1. Брусок A1B1 другой стороной соединен с пружиной жесткостью
с бруском A1B1. Брусок A1B1 другой стороной соединен с пружиной жесткостью  , прикрепленной к стене. Точка F соединения пружины с бруском A1B1 и точка соединения груза с бруском AB выбраны так, что бруски движутся поступательно, т.е.
, прикрепленной к стене. Точка F соединения пружины с бруском A1B1 и точка соединения груза с бруском AB выбраны так, что бруски движутся поступательно, т.е.  . В некоторый момент времени (t=0) груз D отклоняют на величину
. В некоторый момент времени (t=0) груз D отклоняют на величину  вправо от положения, когда пружины не деформированы, и ему сообщается начальная скорость
вправо от положения, когда пружины не деформированы, и ему сообщается начальная скорость  . В тот же момент времени (t=0) точка соединения пружины со стеной начинает движение по закону
. В тот же момент времени (t=0) точка соединения пружины со стеной начинает движение по закону  .
.
Примечание. Положение начала отсчета на оси  соответствует среднему положению стены (
соответствует среднему положению стены (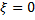 ).
).
| mD, кг | mE, кг | v0, см/с | c 1, Н/см | c 2, Н/см | c 3, Н/см |  ,
кг/с ,
кг/с
|  ,
см ,
см
| p , 1/ с |
| – | – | 1.2 |
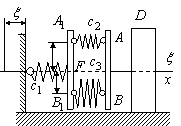
Рис.38
Задача 12. Покоящийся груз D соединен с пружиной (рис.39) жесткостью  , другой конец которой присоединен к бруску AB. Другой стороной брусок AB соединен с параллельными пружинами жесткостью
, другой конец которой присоединен к бруску AB. Другой стороной брусок AB соединен с параллельными пружинами жесткостью  и
и  , которые прикреплены к стене. Точка F соединения пружины с бруском выбрана из условия, что брусок движется поступательно, т.е.
, которые прикреплены к стене. Точка F соединения пружины с бруском выбрана из условия, что брусок движется поступательно, т.е.  . В некоторый момент времени груз отклоняют влево на величину
. В некоторый момент времени груз отклоняют влево на величину  и сообщают ему начальную скорость
и сообщают ему начальную скорость  .
.
| mD, кг | mE, кг | v0, см/с | c 1, Н/см | c 2, Н/см | c 3, Н/см |  ,
кг/с ,
кг/с
|  ,
см ,
см
| p , 1/ с |
| – | – | – | – |

Рис.39
Задача 13. Груз D прикреплен одной стороной к недеформированной пружине (рис.40) жесткостью  , а другой стороной – к системе недеформированных пружин жесткостью
, а другой стороной – к системе недеформированных пружин жесткостью  и
и  . B некоторый момент времени груз отклоняют на величину
. B некоторый момент времени груз отклоняют на величину  влево и одновременно сообщают ему начальную скорость
влево и одновременно сообщают ему начальную скорость  .
.
| mD, кг | mE, кг | v0, см/с | c 1, Н/см | c 2, Н/см | c 3, Н/см |  ,
кг/с ,
кг/с
|  ,
см ,
см
| p , 1/ с |
| 1.5 | – | 4.4 | – | – | – |

Рис.40
Задача 14. Покоящийся груз D присоединен к пружине (рис.41) жесткостью  , соединенной последовательно с пружиной жесткостью
, соединенной последовательно с пружиной жесткостью  , прикрепленной к стене. В некоторый момент времени груз отклоняют на величину
, прикрепленной к стене. В некоторый момент времени груз отклоняют на величину  влево и сообщают ему начальную скорость
влево и сообщают ему начальную скорость  . В тот же момент времени (t=0) точка соединения пружины со стеной начинает движение по закону
. В тот же момент времени (t=0) точка соединения пружины со стеной начинает движение по закону  .
.
Примечание. Положение начала отсчета на оси x соответствует среднему положению стены (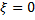 ).
).
| mD, кг | mE, кг | v0, см/с | c 1, Н/см | c 2, Н/см | c 3, Н/см |  ,
кг/с ,
кг/с
|  ,
см ,
см
| p , 1/ с |
| – | – | – | 1.8 |

Рис.41
Задача 15. Пружина А жесткостью c 1 скреплена с невесомым штоком поршня (рис.42), который находится в камере В. В эту камеру попеременно сверху и снизу поступает сжатый воздух, вследствие чего возникает сила, действующая на поршень D, изменяющаяся по закону 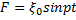 (
( – в ньютонах). В начальный момент (t = 0) поршень был отклонен от положения статического равновесия на расстояние
– в ньютонах). В начальный момент (t = 0) поршень был отклонен от положения статического равновесия на расстояние  вниз и ему была сообщена скорость v0, направленная вниз. Массу штока не учитывать.
вниз и ему была сообщена скорость v0, направленная вниз. Массу штока не учитывать.
| mD, кг | mE, кг | v0, см/с | c 1, Н/см | c 2, Н/см | c 3, Н/см |  ,
кг/с ,
кг/с
|  ,
см ,
см
| p , 1/ с |
| – | – | – | – | – |

Рис.42
Задача 16. К свободному концу В упругой горизонтальной балки (рис.43), другой конец которой закреплен неподвижно, подвешен на пружине груз D, который движется в жидкости. Коэффициент жесткости пружины – с 1, коэффициент жесткости балки – c 2. В начальный момент груз смещен вниз на расстояние  от положения статического равновесия и ему сообщена начальная скорость v0. Сила сопротивления движению груза в жидкости пропорциональна первой степени скорости тела v,
от положения статического равновесия и ему сообщена начальная скорость v0. Сила сопротивления движению груза в жидкости пропорциональна первой степени скорости тела v, 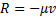 , где
, где  – коэффициент сопротивления. Упругую силу балки считать пропорциональной стреле прогиба, горизонтальным отклонением точки В пренебречь.
– коэффициент сопротивления. Упругую силу балки считать пропорциональной стреле прогиба, горизонтальным отклонением точки В пренебречь.
| mD, кг | mE, кг | v0, см/с | c 1, Н/см | c 2, Н/см | c 3, Н/см |  ,
кг/с ,
кг/с
|  ,
см ,
см
| p , 1/ с |
| – | – | – | – |

Рис.43
Задача 17. К свободному концу В упругой горизонтальной балки (рис.44), другой конец которой закреплен неподвижно, подвешен на пружине груз D с помощью невесомого магнитного стержня, проходящего через соленоид. По соленоиду течет переменный ток, действующий на стержень с вертикальной силой F 1 = 4sin pt (Н), причем р выражено в с– 1. Коэффициент жесткости пружины – с 1, коэффициент жесткости балки – c 2. В начальный момент груз D смещен вниз на расстояние  от положения статического равновесия и отпущен c начальной скоростью v0. Упругая сила балки пропорциональна стреле прогиба, горизонтальным отклонением точки В пренебречь.
от положения статического равновесия и отпущен c начальной скоростью v0. Упругая сила балки пропорциональна стреле прогиба, горизонтальным отклонением точки В пренебречь.
| mD, кг | mE, кг | v0, см/с | c 1, Н/см | c 2, Н/см | c 3, Н/см |  ,
кг/с ,
кг/с
|  ,
см ,
см
| p , 1/ с |
| – | – | – | – | – |

Рис.44
Задача 18. Груз D массы m подвешен на пружине (рис.45), коэффициент жесткости которой равен c 1. Другой конец пружины прикреплен в точке А к пластине, совершающей вертикальные колебания около этой точки по закону  , где р выражено в с– 1, расстояние
, где р выражено в с– 1, расстояние 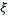 – в сантиметрах, время t – в секундах. В начальный момент груз смещен вниз на расстояние
– в сантиметрах, время t – в секундах. В начальный момент груз смещен вниз на расстояние  от положения статического равновесия и ему сообщена начальная скорость v0.
от положения статического равновесия и ему сообщена начальная скорость v0.
Примечание. Положение начала отсчета на оси x соответствует среднему положению точки А (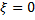 ).
).
| mD, кг | mE, кг | v0, см/с | c 1, Н/см | c 2, Н/см | c 3, Н/см |  ,
кг/с ,
кг/с
|  ,
см ,
см
| p , 1/ с |
| 1.5 | – | – | – | – | 0.5 |

Рис.45
Задача 19. К свободному концу В упругой горизонтальной балки (рис.46), другой конец которой закреплен неподвижно, подвешен на пружине груз D. Коэффициент жесткости балки – с 2, коэффициент жесткости пружины – c 1. В начальный момент груз смещен вниз на расстояние  от положения статического равновесия и имеет скорость v0, направленную вниз. Упругая сила балки пропорциональна стреле прогиба, горизонтальным отклонением точки В пренебречь.
от положения статического равновесия и имеет скорость v0, направленную вниз. Упругая сила балки пропорциональна стреле прогиба, горизонтальным отклонением точки В пренебречь.
| mD, кг | mE, кг | v0, см/с | c 1, Н/см | c 2, Н/см | c 3, Н/см |  ,
кг/с ,
кг/с
|  ,
см ,
см
| p , 1/ с |
| – | – | – | – | – |

Рис.46
Задача 20. Груз D подвешен на трех пружинах (рис.47), как показано на соответствующем рисунке. Коэффициенты жесткости пружин равны c 1, с 2, с 3. В начальный момент груз отклонен от положения статического равновесия вертикально вниз на расстояние  и имеет скорость v0.
и имеет скорость v0.
| mD, кг | mE, кг | v0, см/с | c 1, Н/см | c 2, Н/см | c 3, Н/см |  ,
кг/с ,
кг/с
|  ,
см ,
см
| p , 1/ с |
| – | – | – | – |

Рис.47
Задача 21. На невесомую чашку весов (рис.48), подвешенную на пружинах, с высоты h = 5 см без начальной скорости падает груз D и остается на чашке, не отрываясь от нее. Коэффициенты жесткости пружин равны соответственно c 1 и с 2.
| mD, кг | mE, кг | v0, см/с | c 1, Н/см | c 2, Н/см | c 3, Н/см |  ,
кг/с ,
кг/с
|  ,
см ,
см
| p , 1/ с |
| – | – | – | – | – | – | – |

Рис.48
Задача 22. Груз D подвешен на трех пружинах, как показано на соответствующем рисунке (рис.49). Коэффициенты жесткости пружин равны c 1, с 2, с 3. В начальный момент груз отклонен от положения статического равновесия вертикально вниз на расстояние  и имеет направленную вниз скорость v0.
и имеет направленную вниз скорость v0.
| mD, кг | mE, кг | v0, см/с | c 1, Н/см | c 2, Н/см | c 3, Н/см |  ,
кг/с ,
кг/с
|  ,
см ,
см
| p , 1/ с |
| – | – | – | – |

Рис.49
Задача 23. Груз D, пройдя некоторое расстояние (рис.50), присоединяется с начальной скоростью v0 к невесомому бруску, соединенному с предварительно растянутой с удлинением  пружиной жесткостью c 1.
пружиной жесткостью c 1.
| mD, кг | mE, кг | v0, см/с | c 1, Н/см | c 2, Н/см | c 3, Н/см |  ,
кг/с ,
кг/с
|  ,
см ,
см
| p , 1/ с |
| – | – | – | – | – | – |

Рис.50
Задача 24. К грузу D прикреплены концы двух пружин (рис.51), коэффициенты жесткости которых соответственно равны с 1 и с 2. Концы А и В пружин закреплены неподвижно. Груз может скользить без трения в неподвижных направляющих, расположенных под углом 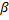 = 30° к вертикали. В начальный момент груз смещен на величину
= 30° к вертикали. В начальный момент груз смещен на величину  от положения статического равновесия и ему сообщена скорость v0.
от положения статического равновесия и ему сообщена скорость v0.
| mD, кг | mE, кг | v0, см/с | c 1, Н/см | c 2, Н/см | c 3, Н/см |  ,
кг/с ,
кг/с
|  ,
см ,
см
| p , 1/ с |
| 1.5 | – | – | – | – |

Рис.51
Задача 25. Груз D прикреплен к горизонтальной крышке с помощью пружины (рис.52) жесткостью с 1. В некоторый момент времени груз отклоняют на величину  из положения статического равновесия вниз и одновременно сообщают ему начальную скорость v0. Сила сопротивления движению пропорциональна первой степени скорости тела v,
из положения статического равновесия вниз и одновременно сообщают ему начальную скорость v0. Сила сопротивления движению пропорциональна первой степени скорости тела v, 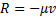 , где
, где  – коэффициент сопротивления.
– коэффициент сопротивления.
| mD, кг | mE, кг | v0, см/с | c 1, Н/см | c 2, Н/см | c 3, Н/см |  ,
кг/с ,
кг/с
|  ,
см ,
см
| p , 1/ с |
| – | – | – | – | – |

Рис.52
Задача 26. Груз D присоединен к стенке с помощью двух пружин (рис.53) жесткостью  и
и  соответственно. В некоторый момент времени (t=0) груз D отклоняют на величину
соответственно. В некоторый момент времени (t=0) груз D отклоняют на величину  вправо от положения, когда пружины не деформированы, и ему сообщается начальная скорость v0. В тот же момент времени (t=0) точка соединения пружины со стеной начинает движение по закону
вправо от положения, когда пружины не деформированы, и ему сообщается начальная скорость v0. В тот же момент времени (t=0) точка соединения пружины со стеной начинает движение по закону  . Сила сопротивления движению пропорциональна первой степени скорости тела v,
. Сила сопротивления движению пропорциональна первой степени скорости тела v, 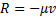 , где
, где  – коэффициент сопротивления.
– коэффициент сопротивления.
Примечание. Положение начала отсчета на оси x соответствует среднему положению стенки (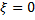 ).
).
| mD, кг | mE, кг | v0, см/с | c 1, Н/см | c 2, Н/см | c 3, Н/см |  ,
кг/с ,
кг/с
|  ,
см ,
см
| p , 1/ с |
| – | – | 1.5 |

Рис.53
Задача 27. Груз D прикреплен к системе двух недеформированных пружин (рис.54) жесткостью  и
и  . В некоторый момент времени груз отклоняют на величину
. В некоторый момент времени груз отклоняют на величину  влево и одновременно сообщают ему начальную скорость
влево и одновременно сообщают ему начальную скорость  . Сила сопротивления движению пропорциональна первой степени скорости тела v,
. Сила сопротивления движению пропорциональна первой степени скорости тела v, 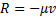 , где
, где  – коэффициент сопротивления.
– коэффициент сопротивления.
| mD, кг | mE, кг | v0, см/с | c 1, Н/см | c 2, Н/см | c 3, Н/см |  ,
кг/с ,
кг/с
|  ,
см ,
см
| p , 1/ с |
| – | – | – | – |

Рис.54
Задача 28. Груз D прикреплен к горизонтальной крышке с помощью двух пружин (рис.55) жесткостью  и
и  соответственно. В некоторый момент времени груз отклоняют на величину
соответственно. В некоторый момент времени груз отклоняют на величину  вниз и одновременно сообщают ему начальную скорость
вниз и одновременно сообщают ему начальную скорость  , направленную вниз. Сила сопротивления движению пропорциональна первой степени скорости v тела,
, направленную вниз. Сила сопротивления движению пропорциональна первой степени скорости v тела, 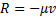 , где
, где  – коэффициент сопротивления. Сопротивлением движению груза по стенке пренебречь.
– коэффициент сопротивления. Сопротивлением движению груза по стенке пренебречь.
| mD, кг | mE, кг | v0, см/с | c 1, Н/см | c 2, Н/см | c 3, Н/см |  ,
кг/с ,
кг/с
|  ,
см ,
см
| p , 1/ с |
| – | – | – | – |

Рис.55

Date: 2015-08-15; view: 1483; Нарушение авторских прав