Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Понятие о фазовой плоскости
|
|
Обычное описание движения системы с одной степенью свободы в виде зависимости координаты от времени x=x(t) не является единственно возможным. В ряде случаев, особенно при изучении нелинейных механических колебаний, определенными достоинствами обладает представление движения на фазовой плоскости.
Состояние системы в любой фиксированный момент времени t определяется парой соответствующих значений x и 
и может быть представлено изображающей (фазовой) точкой в плоской декартовой системе координат x, v, если откладывать по оси абсцисс координату x, а по оси ординат – скорость v. Такая плоскость называется фазовой.
В процессе движения рассматриваемой системы величины x и v изменяются и, соответственно, меняется положение изображающей точки на фазовой плоскости. Геометрическое место изображающих точек для данного движения называется фазовой траекторией.
Для построения фазовой траектории при заданном законе движения x=x(t) нужно путем дифференцирования образовать выражение скорости v =x(t), а затем исключить время из двух уравнений: x=x(t),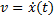 
.
Функция v = v (x) и описывает фазовую траекторию данного движения.
Фазовая плоскость особенно удобна для представления колебательных процессов, когда координата и скорость не выходят за известные пределы; поэтому вся картина движения даже в течение неограниченного времени занимает ограниченную часть фазовой плоскости.
Совокупность фазовых траекторий, которая описывает все возможные движения данной системы, называется фазовой диаграммой (фазовым портретом) данной системы.
Для свободных гармонических колебаний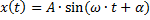 
, а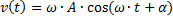 
. Исключая из этих выражений время t получаем
Это уравнение эллипса (рис.11). Его полуоси зависят от амплитуды и круговой частоты.
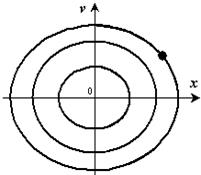
Рис.11
Date: 2015-08-15; view: 565; Нарушение авторских прав