Амплитуда при резонансе

а резонансная частота

Рис.16.1

Резонанс играет большую роль в природе, науке и технике. Резонанс сооружений и машин при периодических внешних воздействиях может являться причиной катастроф. Чтобы избежать резонансного воздействия, подбирают соответствующим образом свойства системы или используют успокоители колебаний, основанные на явлении антирезонанса. В радиотехнике благодаря резонансу можно отделить сигналы одной (нужной) радио- или телестанции от всех других.

Свободные колебания с вязким сопротивлением.

Существуют устройства (демпферы), которые создают силу пропорциональную относительной скорости (рис.17). Коэффициент пропорциональности называется коэффициентом демпфирования или коэффициентом вязкого сопротивления.

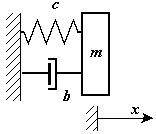
Рис.17

Дифференциальное уравнение движения точки с массой m, закрепленной на упругом элементе и демпфере имеет вид:

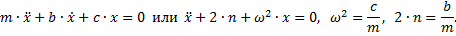
Начальные условия имеют вид: t=0,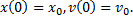

Характеристическое уравнение имеет вид: .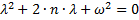

Корни характеристического уравнения равны:

Рассмотрим возможные решения:

1-й случай

Решение имеет вид:

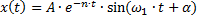
- условная амплитуда затухающих колебаний;

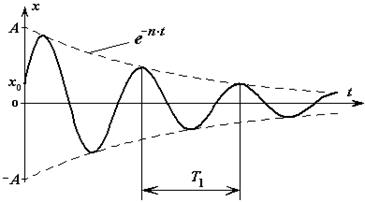
Рис.18

- круговая или циклическая частота затухающих колебаний. Измеряется в рад/сек.

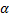- фазовый угол (или просто фаза).

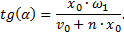
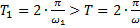- период затухающих колебаний (рис.18).

- частота колебаний (1 колеб/cек=1 Гц)

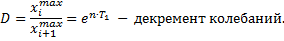
- логарифмический декремент колебаний.

Материальная точка совершает гармонические колебания с частотой и амплитудой, величина которой все время убывает.

Движение изображающей точки на фазовой плоскости показано на рис. 19.

Рис.19

2-й случай

Решение имеет вид:

Материальная точка совершает затухающее неколебательное движение (рис.39).

Рис.20

3-й случай 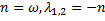(два одинаковых корня)

Решение имеет вид:

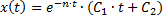
Материальная точка так же совершает затухающее неколебательное движение (рис.20).

Date: 2015-08-15; view: 679; Нарушение авторских прав