Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Теорема об изменении кинетической энергии точки
|
|
Рассмотрим точку с массой т, перемещающуюся под действием приложенных к ней сил из положения M 0, где она имеет скорость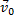 
, в положение М 1, где ее скорость равна 
.
Для получения искомой зависимости обратимся к уравнению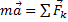 
выражающему основной закон динамики. Проектируя обе части этого равенства на касательную 
к траектории точки М, направленную в сторону движения, получим:
Стоящую слева величину касательного ускорения можно представить в виде
В результате будем иметь:
Умножив обе части этого равенства на ds, внесем т под знак дифференциала. Тогда, замечая, что 
где 
- элементарная работа силы Fk получим выражение теоремы об изменении кинетической энергии в дифференциальной форме:
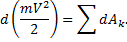
Проинтегрировав теперь обе части этого равенства в пределах, соответствующих значениям переменных в точках M 0 и M 1, найдем окончательно:
Уравнение выражает теорему об изменении кинетической энергии точки в конечном виде: изменение кинетической энергии точки при некотором ее перемещении равно алгебраической сумме работ всех действующих на точку сил на том же перемещении.
Пример 7. По графику зависимости скорости от времени v (t) определить, является ли работа силы, действующей на материальную точку в интервале времени от 0 до τ положительной, отрицательной, равной нулю (рис.13). Учесть, что АО = ОВ.
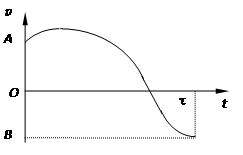
Рис.13
Решение. Работа силы, действующей на частицу, равна приращению кинетической энергии частицы.
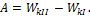
Кинетическая энергия материальной точки связана со скоростью соотношением 
Поскольку скорости частицы в моменты времени t=0 и t=τ согласно условию задачи равны по величине (на графике АО = ОВ), то и кинетические энергии в этих состояниях одинаковы, т.е. 
Следовательно, работа приложенной силы за указанный промежуток времени равна нулю.
Пример 8. Точка движется по оси Ox под действием силы, направленной вдоль оси x (рис.14). Сравните значения кинетической энергии точки в начальном и конечном состояниях для случаев, когда проекция силы на ось координат изменяется согласно графикам “а” и “б”?
Рис.14
Решение. Согласно теореме приращение кинетической энергии частицы равно работе силы, действующей на частицу.
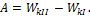
Работа переменной силы определяется соотношением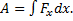 
Учитывая геометрический смысл интеграла (площадь криволинейной трапеции), нетрудно видеть, что в случае “а” работа равна нулю и кинетические энергии начального и конечного состояний совпадают. В случае “б” работа положительна и кинетическая энергия конечного состояния больше, чем начального.
Пример 9. Два диска с равными массами, на разных размеров (R A = 2 R B) раскручивают до одинаковых угловых скоростей. Найти отношения произведенных работ.
Решение. Работа по раскручиванию диска равна приращению кинетической энергии, т.е. A=∆Wk. Начальная кинетическая энергия каждого диска равна нулю, конечная связана с угловой скоростью формулой
Учитывая, что момент инерции сплошного однородного диска равен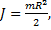 
получим искомое отношение произведенных работ:
Date: 2015-08-15; view: 530; Нарушение авторских прав