Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Следовательно, работа силы потенциального поля не зависит от траектории движения точки, а определяется лишь значениями силовой функции в начальном и конечном положениях точки
|
|
Естественно, если точка вернется в начальное положение, работа силы 
будет равна нулю. Работа окажется равной нулю и при переходе в другую точку М 3, если там значение силовой функции будет такое же, как и в начальном положении.
Нетрудно догадаться, что точки с одинаковыми значениями силовой функции будут образовывать целую поверхность. И что силовое поле – это слоеное пространство, состоящее из таких поверхностей (рис. 8). Эти поверхности называются поверхностями уровня или эквипотенциальными поверхностями. Уравнения их: u(x, y, z)=C (C – постоянная, равная значению u в точках этой поверхности). А силовую функцию называют, соответственно, потенциалом поля.
Конечно, эквипотенциальные поверхности не пересекаются. Иначе существовали бы точки поля с неопределенным потенциалом.
Поскольку, при перемещении точки по эквипотенциальной поверхности работа силы равна нулю, то вектор силы перпендикулярен поверхности.
Выберем среди этих поверхностей какую-нибудь одну и назовем ее нулевой поверхностью (положим у нее u=u0).
Работа, которую совершит сила при переходе точки из определенного места М на нулевую поверхность, называют потенциальной энергией точки в этом определенном месте М:
Если тело находится в потенциальном поле сил, то оно будет обладать потенциальной энергией. Потенциальную энергию тела, связанного с нулевым уровнем системы отсчета, принимают нулевой, а энергию других положений отсчитывают относительно нулевого уровня.
По (8) силовая функция 
. Поэтому проекции силы на декартовы оси, по (6), так как 
,
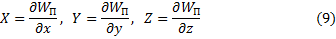
и вектор силы 
.
Рассмотрим несколько потенциальных полей.
1) Поле силы тяжести.
Вблизи поверхности Земли сила тяжести во всех точках одинакова 
, равна весу тела. Значит, это силовое поле однородное. Так как при перемещении точки в горизонтальной плоскости работа силы равна нулю, то эквипотенциальными поверхностями будут горизонтальные плоскости (рис. 9), а уравнения их: u = z = C.
Рис.9
Если нулевой поверхностью назначить плоскость xOy, то потенциальная энергия точки в положении М будет равна работе силы тяжести:
WП=A=Ph=mgh.
это энергия тела, поднятого над Землей на высоту h.
Так как начало отсчета выбирается произвольно, то W П может в общем случае принимать и отрицательные значения (например, W П на дне шахты).
2 ) Поле упругой силы.
При деформации упругого тела, например пружины, появляется сила. То есть около этого тела возникает силовое поле, силы которого пропорциональны деформации тела и направлены в сторону недеформированного состояния. У пружины – в точку М 0, где находится конец недеформированной пружины (рис. 10).
Рис.10
Если перемещать конец пружины так, чтобы длина ее не изменялась, то работа упругой силы будет равна нулю. Значит эквипотенциальными поверхностями являются сферические поверхности с центром в точке О.
Назначим нулевой поверхностью сферу, проходящую через точку М 0, через конец недеформированной пружины. Тогда потенциальная энергия пружины в положении М: WП=A=0,5kx2.
При таком выборе нулевой поверхности потенциальная энергия всегда будет положительной (WП>0), и в растянутом, и в сжатом состоянии.
Полная механическая энергия системы равна энергии механического движения и энергия взаимодействия:
Полная механическая энергия тела при его перемещении вдоль любой траектории в потенциальном поле остается постоянной.
Пример 1. Рассмотрим свободное падение камня массой m, брошенного в поле гравитации Земли из точки 1 в точку 2 (рис. 11).
Рис.11
Элементарная работа, совершаемая силой тяжести при перемещении камня, равна:
Полная работа на участке 1–2 находится как
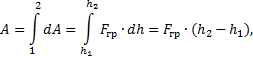
где F гр = mg – сила тяжести; тогда получаем:
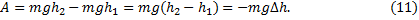
Из последнего выражения видно, что работа определяется только положением начальной и конечной точек траектории тела.
Пример 2. Найдем потенциальную энергию упруго деформированного тела (пружины). Известно, что сила упругости пропорциональна деформации x:
где k – коэффициент упругости; x – значение деформации; знак (–) указывает, что Fупр направлена в сторону, противоположную деформации.
Для преодоления силы упругости необходимо приложить силу:
Элементарная работа – работа, совершаемая при бесконечно малой деформации:
Полная работа найдется как
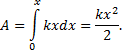
Работа в данном примере идет на увеличение потенциальной энергии пружины. Если при x = 0 Won = 0, то с = 0. Потенциальная энергия упругодеформированного тела равна
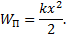
Пример 3. Материальная точка массой m движется по оси Ох в потенциальном силовом поле с энергией, зависящей от координаты x по закону: W р= -αx4, где α - положительная постоянная. Найти зависимость ускорения точки от координаты x.
Решение. Используя связь между силой и потенциальной энергией:
найдем зависимость силы от координаты x:
По второму закону Ньютона получим выражение для ускорения:
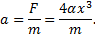
Если аналитически или графически задана зависимость потенциальной энергии от угла поворота при вращательном движении, то, применяя соотношение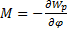 
, можно выразить момент силы, а также найти угловое ускорение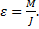 
Пример 4. Вагон массой m = 20 т, двигаясь равнозамедленно с начальной скоростью v 0 = 54 км/ч, под действием силы трения Fmp = 6 кН через некоторое время останавливается. Найти работу A сил трения и расстояние S, которое вагон пройдет до остановки.
Date: 2015-08-15; view: 1142; Нарушение авторских прав