Консервативные силы

Лекция 2. Работа. Мощность. Теорема об изменении кинетической энергии точки.

В данной лекции рассматриваются следующие вопросы:

1. Работа силы.

2. Консервативные силы.

2. Мощность.

3. Примеры вычисления работы.

4. Потенциальная энергия

5. Кинетическая энергия

6. Теорема об изменении кинетической энергии точки.

7. Теорема моментов.

Изучение данных вопросов необходимо для динамики движения центра масс механической системы, динамики вращательного движения твердого тела, кинетического момента механической системы, для решения задач в дисциплинах «Теория машин и механизмов» и «Детали машин».

Работа силы. Мощность.

Для характеристики действия, оказываемого силой на тело при некотором его перемещении, вводится понятие о работе силы.

Рис.1

При этом работа характеризует то действие силы, которым определяется изменение модуля скорости движущейся точки.

Введём сначала понятие об элементарной работе силы на бесконечно малом перемещении ds. Элементарной работой силы (рис.1) называется скалярная величина:

,

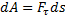где - проекция силы на касательную к траектории, направленную в сторону перемещения точки, а ds- бесконечно малое перемещение точки, направленное вдоль этой касательной.

Данное определение соответствует понятию о работе, как о ха­рактеристике того действия силы, которое приводит к изменению модуля скорости точки. В самом деле, если разложить силу на составляющие 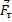и 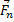, то изменять модуль скорости точки будет только составляющая 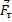, сообщающая точке касательное ускорение. Составляющая же 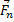или изменяет направление вектора скорости v (сообщает точке нормальное ускорение), или, при несвободном дви­жение изменяет давление на связь. На модуль скорости составляю­щая 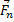влиять не будет, т.е., как говорят, сила 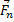«не будет про­изводить работу».

Замечая, что 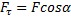, получаем:

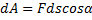. (1)

Таким образом, элементарная работа силы равна проекции силы на направление перемещения точки, умноженной на элементар­ное перемещение ds или элементарная работа силы равна произведению модуля силы на элементарное перемещение ds и на косинус угла между направлением силы и направлением перемещения.

Если угол 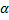острый, то работа положительна. В частности, при 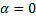элементарная работа dA=Fds.

Если угол 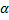тупой, то работа отрицательна. В частности, при элементарная работа dA=-Fds.

Если угол , т.е. если сила направлена перпендикулярно перемещению, то элементарная работа силы равна нулю.

Положительную силу F (α> 90°) называют движущей, а отрицательную (α> 90°) – силой сопротивления.

Найдем аналитическое выражение элементарной работы. Для этого разложим силу на составляющие по направлениям координатных осей (рис.2; сама сила на чертеже не показана).

Рис.2

Элементарное перемещение слагается из перемещений dx, dy, dz вдоль координатных осей, где x, y, z - координаты точки М. Тогда работу силы на перемещении ds можно вычислить как сумму работ её составляющих на перемещениях dx, dy, dz.

Но на перемещении dx совершает работу только составляющая 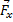, причем её работа равна F_xdx. Работа на перемещениях dy и dz вычисляется аналогично.

Окончательно находим: dA=F_xdx+F_ydy+F_zdz.

Формула дает аналитическое выражение элементарной работы силы.

Работа силы на любом конечном перемещении М ₀ М ₁ вычисляется как интегральная сумма соответствующих элементарных работ и будет равна:

Следовательно, работа силы на любом перемещении М ₀ М ₁ равна взятому вдоль этого перемещения интегралу от элементарной работы. Пределы интеграла соответствуют значениям пере­менных интегрирования в точках М ₀ и М ₁. Графически площадь под всей кривой М ₀ и М ₁ и будет искомой работой.

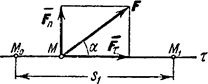
Рис.3

Если величина постоянна (, то и обозначая перемеще­ние М ₀ М ₁ через 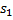получим: .

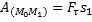Такой случай может иметь место, когда действующая сила постоянна по модулю и направлению (F = const), а точка, к ко­торой приложена сила, движется прямолинейно (рис.3). В этом случае и работа силы .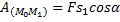

Единицей измерения работы в системе СИ является джоуль (1 дж= 1 Н∙м). 1 Дж – работа, совершаемая силой 1 Н на 1 м пути.

Консервативные силы.

Силы, действующие на тело, могут быть консервативными и неконсервативными. Сила называется консервативной или потенциальной, если работа, совершаемая этой силой при перемещении материальной точки из одного положения в другое, не зависит от вида траектории (формы пути) и определяется только начальным и конечным положениями тела (рис.3.1): А _1В2 = А _1С2 = А ₁₂.

Рис.3.1

В случае, если тело движется в обратном направлении А ₁₂= – А ₂₁, т.е. изменение направления движения по траектории на противоположное вызывает изменение знака работы. Следовательно, при движении материальной точки по замкнутой траектории работа консервативной силы равна нулю (например, поднятие и опускание груза):

Консервативными силами являются силы гравитационного взаимодействия, силы упругости, электростатические силы. Силы, не удовлетворяющие условию (1), называются неконсервативными. К неконсервативным силам относят силы трения и сопротивления. Поле, в котором действуют консервативные силы, называется потенциальным.

Date: 2015-08-15; view: 466; Нарушение авторских прав