Дифференциальные уравнения равновесия жидкости

(уравнения Эйлера)

Рассмотрим равновесие жидкости (рис.11). Возьмем точку А и выделим около нее прямоугольный параллелепипед со сторонами 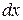, , 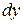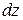. Обозначим внешние силы, отнесенные к единице массы через 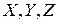. Внешними силами здесь будут:

- объемные, пропорциональные массе параллелепипеда;

- силы гидростатического давления, действующие на грани параллелепипеда со стороны окружающей жидкости.

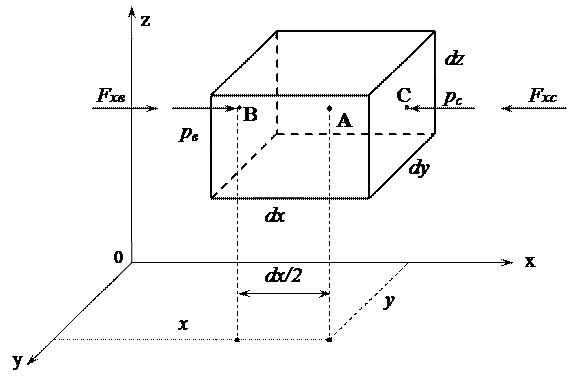Рисунок 11 – К выводу уравнений Эйлера

Рассмотрим сначала силы, действующие на жидкий параллелепипед по оси х.

Проекция объемных сил 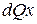на ось х будет равна:

;

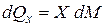Следовательно, проекции объемных сил на все оси:

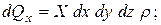
Гидростатическое давление в точке В обозначим , а в точке С - через . Если давление изменяется по линейному закону и непрерывно, тогда:

;

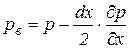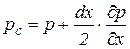
где 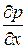- градиент гидростатического давления;

р - давление в точке А.

Силы, действующие на грани равны:

;

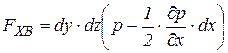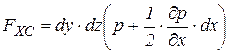
Составим уравнение равновесия исследуемого нами жидкого объема относительно оси X:

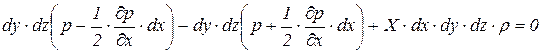
Уравнение равновесия после подстановки и преобразования сможем записать в виде:

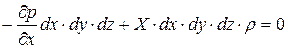
Окончательно уравнение равновесия относительно оси X будет иметь вид:

Аналогично получим уравнение равновесия относительно осей Y и Z и запишем полную систему уравнений, которые называются уравнениями Эйлера.

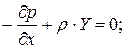
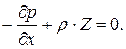
Впервые они были выведены в 1775 г. и выражают закон распределения гидростатического давления в дифференциальной форме.

Для дальнейшего преобразования, умножим каждое из уравнений системы на 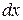, , 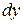, 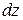соответственно

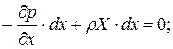
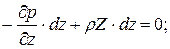
а, сложив их почленно, получим следующее выражение:

.

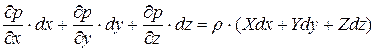Левая часть представляет полный дифференциал давления dp функции . А так как левая часть - полный дифференциал функции, то и правая тоже. Только в этом случае уравнение может иметь смысл. Для этого необходимо, чтобы существовала функция , производные которой были равны:

; ; .

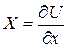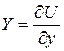Функция 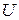и обратная ей функция 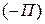называются потенциальными. Следовательно, поле массовых сил потенциальное или 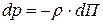, где функция 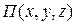выражает потенциальную энергию поля массовых сил (сил тяжести и инерции).

Интегрируя функцию 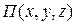для несжимаемой жидкости, получаем:

или ,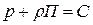

где С - постоянная интегрирования.

Для двух точек одного и того же объема данной однородной несжимаемой жидкости уравнение записывается в виде:

.

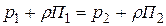Дадим определение поверхности равного давления: это поверхность, проведенная в покоящейся жидкости таким образом, что давление во всех ее точках одинаково, т.е. . Поверхности равного давления обладают следующими основными свойствами:

-построенные для различных гидростатических давлений, они не имеют общих точек, т.е. не пересекаются;

-они всегда нормальны к направлению равнодействующей внешних объемных сил, приложенных к жидкости.

Date: 2015-08-15; view: 884; Нарушение авторских прав