Вопрос: Шар и сфера, их сечения. Взаимное расположение плоскости и шара. Формулы объёма шара и площади сферы

Шар — геометрическое тело; совокупность всех точек пространства, находящихся от центра на расстоянии, не больше заданного. Это расстояние называется радиусом шара.

Площадь поверхности 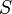и объём 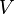шара радиуса определяются формулами:

, ,

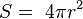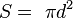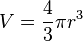
Сфера — замкнутая поверхность, геометрическое место точек в пространстве, равноудалённых от данной точки, называемой центром сферы.

Площадь сферы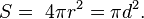

Объём шара, ограниченного сферой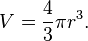

Площадь сегмента сферы 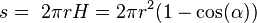, где H — высота сегмента, а 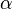— зенитный угол

25 Вопрос: Прямоугольная (декартова) система координат в пространстве. Компланарные векторы. Расположение по трём некомпланарным векторам.

Возьмем три взаимно перпендикулярные прямые x, y, z, пересекающиеся в одной точке 0 и зададим на каждом из них направление. Получится Декартова система координат. Прямые x, y, z – координатные оси, точка 0 – начало координат.

Три вектора (или большее число) называются компланарными, если они, будучи приведенными к общему началу, лежат в одной плоскости

Если вектор с можно разложить по векторам а и b, т.е. представить в виде c = xa+yb, где x и y – некоторые числа, то векторы a, b и c компланарны.

Три некомпланарных вектора 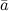, 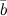и 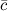, приведенных к общему началу, образуют так называемую связку трех векторов (или тройку векторов).

Тройка векторов называется упорядоченной, если четко сказано, какой вектор в ней идет первым, и так далее.

Тройка векторов 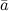, 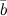и 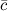называется левой, если поворот от вектора 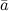к вектору 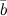, видимый с конца третьего вектора 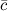, осуществляется по ходу часовой стрелки.

Тройка векторов 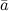, 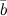и 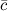называется правой, если поворот от вектора 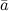к вектору 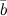, видимый с конца третьего вектора 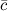, осуществляется против хода часовой стрелки

Date: 2015-08-15; view: 812; Нарушение авторских прав