Предельная точка прямой. Линия горизонта

Для построения изображения бесконечно удаленной точки F_∞ прямой АВ необходимо провести луч зрения через эту точку, Рис. 6. Но тогда луч зрения станет параллелен самой прямой, а точка его пересечения с картинной плоскостью будет служить центральной проекцией бесконечна удаленной точки этой прямой. Из хода построений вытекает, что проекция прямой АВ не может быть продолжена на картине дальше точки F_∞k, точка F_∞k называется предельной точкой прямой.

Из построения можно заметить, что для любой прямой, лежащей в предметной плоскости, предельная точка отстоит от основания картины на расстояние, равное высоте точки зрения.

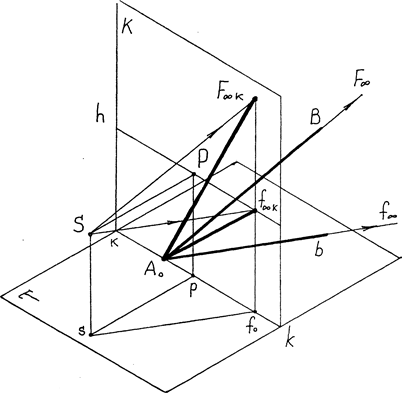
Рис.6.Начальная и предельная точки прямой

Отсюда следует, что совокупность предельных точек всех прямых, лежащих в предметной плоскости, представит на картине прямую, расположенную параллельно основанию картины и отстоящую от него на расстояние, равное высоте точки зрения. Эта прямая является предельной прямой предметной плоскости. Она представляет перспективу бесконечно удаленной прямой предметной плоскости и ограничивает на картине изображение предметной плоскости со всеми точками и линиями, ей принадлежащими. Предельная прямая предметной плоскости является на картине линией горизонта – h-h.

Линия горизонта, главная точка картины и основание картины являются основными элементами перспективного изображения, служащими опорой для правильного построения изображения на картинной плоскости.

На Рис.7, изображена отдельно от проецирующего аппарата плоскость картины К с нанесенными на ней основанием картины, линией горизонта и главной точкой Р.

Наличие на картине указанных элементов дает возможность получить основные сведения о взаимном расположении элементов проецирующего аппарата. Линия горизонта и линия основания ограничивают часть картинной плоскости, на которую проецируются точки предметной плоскости, а также точки предметного пространства, расположенные ниже плоскости горизонта.

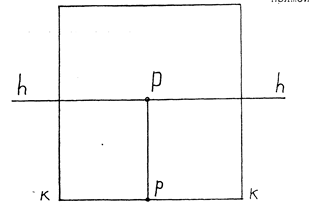
Рис.7. Плоскость картины

5. ПОСТРОЕНИЕ ПЕРСПЕКТИВЫ ТОЧКИ ПО ЕЕ

ОРТОГОНАЛЬНЫМ ПРОЕКЦИЯМ.

На Рис.8, заданы ортогональные проекции точки А, представленной в системе двух взаимно перпендикулярных плоскостей проекций. На этом же чертеже дана проекция картинной плоскости К, расположенной перпендикулярно к горизонтальной плоскости проекций Н, заданной своим следом k-k, а также проекции точки зрения S. Центральные проекции точки А могут быть получены, как точки пересечения лучей зрения, проведенных из точки зрения через точку А и ее основание, с горизонтальнопроецирующей картинной плоскостью К.

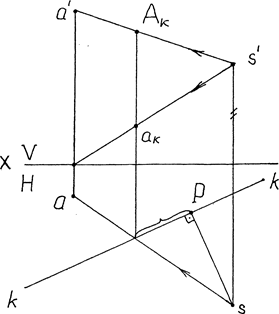
Рис. 8.Ортогональные проекции тонки и системы перспективных координат

На Рис. 9. изображена, заданная отдельно картинная плоскость К, с построенной на ней перспективой точки А. Положение центральных проекций точки А относительно основания картины определено по фронтальной проекции на Рис.8. Положение линии связи определено по отношению к главной точке картины – P. Перспектива прямой линии по ее заданным ортогональна проекциям может быть определена по перспективам двух точек – концов ее отрезка так, как это показано на Рис.8.

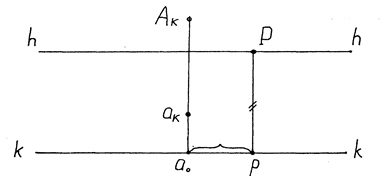
Рис. 9. Перспектива точки, построенная по ее ортогональным проекциям

Date: 2015-07-27; view: 1184; Нарушение авторских прав