Вывести соотношение для угла наименьшего отклонения луча в призме

Ход лучей в призме. На одну из поверхностей призмы, показатель преломления которой относительно окружающей среды есть n, падает луч под углом i₂. Исходя из закона преломления, построим ход луча в призме (рис. 5.1). Угол между преломляющими поверх­ностями обозначим через А. (преломляющий угол призмы). Ли­ния пересечения преломляющих поверхностей называется прелом­ляющим ребром. Плоскость, перпендикулярную этому ребру, принято называть главным сечением призмы. Угол между продол­жениями падающего и вышедшего (под углом и) лучей обозначим через φ (угол отклонения луча в призме). Так как φ есть внешний угол треугольника BCD, то 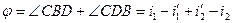. Как видно из Рис. 7.22, 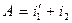. Тогда для угла отклонения имеем 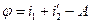. Согласно закону преломления, и 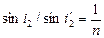. Отсюда

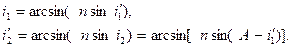(5.1)

Подставляя значения 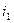и 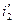в выражение для φ, имеем

(5.2)

Найдем минимальное значение угла отклонения. Легко доказать, что 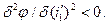Следовательно, 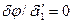есть условие минимума. Тогда

. (5.3)

Это равенство имеет место пр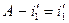и и 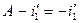. Поскольку 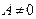, то физический смысл имеет только условие 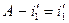, откуда следует, что 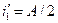. Так как 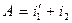, то 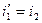- т.е. угол отклонения минимален при симметричном расположе­нии падающего на призму и вышедшего из нее лучей (когда луч внутри призмы параллелен ее основанию). Следовательно, для φ_мин получаем

φ_мин=2 arcsin (n sin A/2)–A. (5.4)

Отсюда

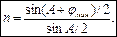(5.5)

Date: 2015-08-07; view: 2173; Нарушение авторских прав