Групповая скорость

Можно было бы ограничиться только по­нятием фазовой скорости, если бы монохроматические волны ре­ально существовали. Однако отдельные атомы излучают в дейст­вительности не бесконечные во времени монохроматические волны, а своего рода световые импульсы. Подобный «световой импульс может быть смоделирован в виде «кусочка» монохроматической волны длительности ∆t, как это показано на рис.2.4. Немонохро­матичность световых волн и обусловлена в основном обрывом моно­хроматической волны.

Как увидим в дальнейшем (см. § 4 и 5 этой главы), конечные импульсы можно представить в виде совокупности гармонических колебаний с разными амплитудами, частотами и фазами. Пусть ∆ω — интервал, в пределах которого лежат упомянутые частоты. Ширина интервала ∆ω зависит от длительности импульса. Можно показать, что интервал частот обратно пропорционален длитель­ности импульса, т. е.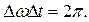

Форма импульса определяется частотами, амплитудами и фазами его гармонических составляющих. Если скорости всех этих составляющих одинаковы, то их фазовые со­отношения не меняются при распростра­нении и, следовательно, форма импульса также остается неизменной. В этом слу­чае скорость перемещения импульса сов­падает со скоростью его гармонических составляющих. Среда, в которой фазо­вая скорость гармонической волны не зависит от частоты, называется недиспергирующей. В случае, если скорости

.РИС(4.11) гармонических волн зависят от частоты, фазовые соотношения между ними меняются по мере их распространения, что приводит к изме­нению формы импульса. Отсюда следует, что скорость перемещения импульса и фазовая скорость его гармонических составляющих не совпадают. В этом случае распространение импульса характери­зуют с помощью так называемой групповой скорости. Среда, в ко­торой фазовая скорость зависит от частоты, называется диспер­гирующей.

Введем групповую скорость для случая простейшей группы, состоящей из двух гармонических составляющих одинаковой ам­плитуды, мало отличающихся по частоте и распространяющихся вдоль оси х:

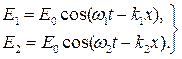(4.40)

Результирующая волна будет иметь вид

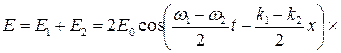
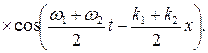(4.41)

По условию,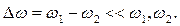

Учитывая это, получим

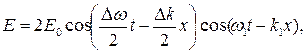(4.42)

Где 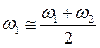и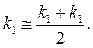

Полученное выражение (2.24) для сложной волны можно при­ближенно считать уравнением монохроматической волны с часто­той co_1? волновым числом &i и медленно меняющейся (модулиро-

ванной) амплитудой

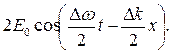(4.43)

Если такой модулированный по амплитуде импульс принимается спектральным приоо-ром, то он будет регистрировать две частоты: ω₁ и ω₂.

Модулированная амплитуда характеризует группу волн. По­этому распространение импульса можно характеризовать скоростью переноса определенного значения модулированной амплитуды. Эту скорость называют групповой скоростью волн. Так как на опыте удобно регистрировать максимальную амплитуду, то под групповой скоростью понимают скорость перемещения максимума амплитуды волны. Следовательно, групповая скорость определяется из усло­вия

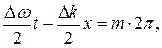(4.44)

где т — любое целое число. После дифференцирования (2.25) по t получим

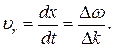(4.45)

В пределе можно перейти к дифференциалу:

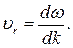(4.46)

Связь между фазовой и групповой скоростями. Исходя из (2.26) и (2.22) можно найти связь между фазовой и групповой скоростями:

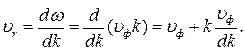(4.47)

Так как 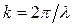и отсюда 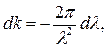то из (2.27) имеем 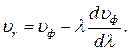(4.48)

Полученное выражение (2.28) носит название формулы Рэлея. Им же было впервые введено понятие групповой скорости.

Date: 2015-08-07; view: 607; Нарушение авторских прав