САУ с ассоциативной памятью

В системах управления может быть организована и использована ассоциативная память. Ассоциативная память – это средство хранения информации на основе ассоциации, т.е. её извлечение по сочетанию определённых признаков.

Различают [8] пирамидальную (иерархическую), матричную и самоорганизующуюся память.

Пирамидальная память осуществляет классификацию входного информационного вектора по одному признаку, затем по-другому и так до тех пор, пока все признаки не совпадут с какой-либо классификационной группой.

Матричная память – это один уровень пирамидальной ассоциативной памяти. Она реализуется на логических элементах и нейросетях.

Самоорганизующаяся память хранит информацию в виде аттракторов, на один из которых выходит система.

Интеллектуальные системы с ассоциативной памятью могут работать в условиях предсказуемой и непредсказуемой неопределённости. В первом случае обучение системы происходит автоматически, поскольку известна заранее информация о поле, в котором меняются координаты объекта управления. Во втором случае в процессе первичного обучения участвует оператор. После того, как произведено первичное обучение, ассоциативная память заменяет человека и далее осуществляется автоматическая подстройка структуры и параметров объекта управления. При использовании ассоциативной памяти уменьшается её объём и повышается быстродействие системы в целом.

4.2.4. Системы управления с нечёткой логикой

Рассмотрим особенности систем управления с нечёткой логикой [8, 9]. Системы с нечёткой логикой (Fussy-Logic) создают для управления сложными трудно формализуемыми и слабо структурированными процессами. При этом используется опыт специалистов-экспертов.

К основным понятиям фаззи-логики относятся нечёткое множество и лингвистическая переменная.

Под нечётким множеством 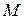понимают подмножество 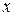множества 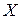, которое определяется непрерывной функцией принадлежности 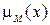могущей принимать значения от 0 до 1. Нечеткое множество 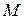может задаваться так:

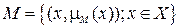. (4.2)

Лингвистическая переменная – это переменная, которая задаётся нечёткими словами или предложениями. Отдельное лингвистическое значение (терм) определяется одной функцией принадлежности. Для описания лингвистических переменных в ТАУ может применяться набор до семи термов, созданных словами: отрицательный (n egative), нулевой (z ero), положительный (p ositive), большой (b ig), средний (m iddle), малый (s mall), изображённых треугольными и трапецеидальными функциями принадлежности на рис. 4.4.

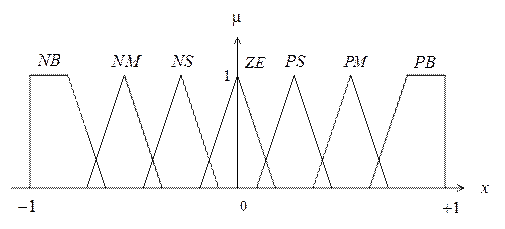
Рис. 4.4

Минимальный набор термов – три: N, ZE, P, но при этом осуществляется грубая декомпозиция входного пространства на подмножества.

Процедуру определения значения функции принадлежности 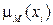, соответствующего конкретному значению 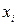переменной 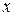, называют фаззификацией. Другими словами: под фаззификацией понимают преобразование чётких значений переменных в нечёткие.

Операции с нечёткими множествами используют известные в алгебре чёткой логики операции «И», «ИЛИ», «НЕ» с той разницей, что вместо истинности переменных (0 и 1) применяют функции принадлежности.

Операция конъюнкция («И») осуществляется с помощью минимизации:

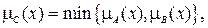(4.3)

где нечёткое множество 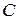называется фаззи-пересечением нечётких множеств 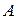и :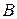

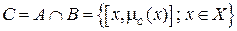. (4.4)

Операция дизъюнкции («ИЛИ») осуществляется с помощью максимизации:

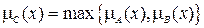, (4.5)

где нечётное множество 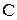- фаззи-объединение нечётких множеств 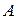и :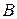

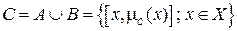. (4.6)

На рис. 4.5, а показана функция принадлежности фаззи-пересечения множеств ZE и P, а на рис. 4.5, б – функция принадлежности фаззи-объединения этих множеств.

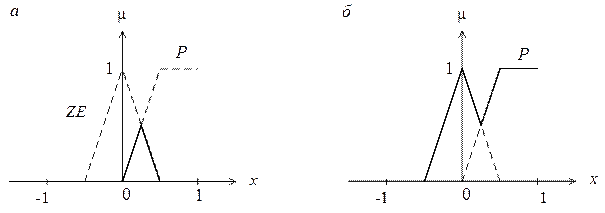
Рис. 4.5

Важнейшей операцией фаззи-логики является операция нечёткого вывода. Она основана на ряде композиционных операторов. Рассмотрим операцию импликации (связывания). Она заключается в соединении двух нечётких множеств 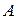и 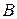по правилу «ЕСЛИ 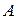ТО 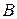», причём множества 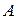(посылка) и 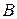(заключение) определены на разных базисных множествах 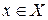и .

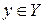Множество, соответствующее правилу «ЕСЛИ 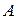ТО 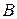», образуется из пар 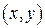, относящихся к новому базисному множеству

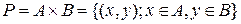. (4.7)

Связь между множествам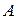и и 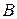устанавливается с помощью отношения

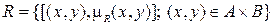, (4.8)

где 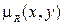- функция принадлежности пар 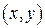из декартова произведения 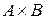к подмножеству, образованному по определённому правилу .

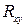Функцию принадлежности 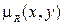можно определить с помощью операции минимизации:

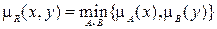. (4.9)

Функцию принадлежности 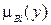при конкретном значении 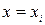можно определить двумя способами:

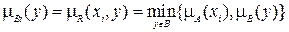, (4.10)

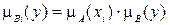. (4.11)

Рис. 4.6 иллюстрирует эти случаи: трапеция 1 соответствует формуле (4.10), а треугольник 2-формуле (4.11).

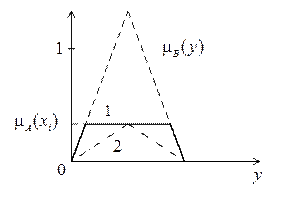
Рис. 4.6

Нечёткое множество 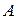может представлять также пересечение или объединение нескольких множеств.

Рассмотри следующую операцию - агрегирование, т.е. композицию нескольких правил «ЕСЛИ 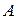ТО 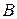», связанных через «ИЛИ». Оно осуществляется максимизацией функций принадлежности всех объединённых правил.

Результирующая функция принадлежности нечёткого множества 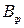величины 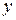при .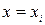

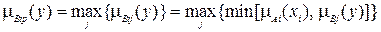, (4.12)

где 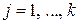- номер правила; 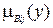- функция принадлежности заключения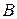 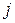-го правила, ограниченная значением 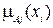(рис. 4.6); 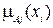и 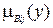- функции принадлежности соответственно посылки 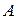и заключения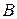 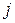-го правила.

Для определения конкретных значений 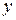по полученной результирующей функции принадлежности (4.12) проводится дефаззификация. Дефаззификация преобразует нечёткие величины в чёткие. В настоящее время при дефаззификации чаще всего используют два метода: метод центра тяжести и метод максимума [9].

В первом случае чёткое значение выходной переменной

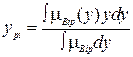, (4.13)

а для дискретных пространств

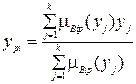. (4.14)

Во втором случае (метод максимума)

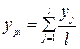, (4.15)

где 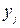- выходная переменная, для которой функция принадлежности достигла максимума, а 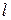- число таких величин.

Из этих двух методов первый даёт приемлемые результаты для установившихся режимов, а второй - для переходных режимов [9].

Простейшие примеры реализации основных процедур фаззи-логики применительно к нечётким системам управления приведены в [8, 9].

В настоящее время в теории систем управления развиваются и другие подходы. Среди них выделяются теории катастроф и детерминированного хаоса.

Теория катастроф основана на объединении теории гладких отображений и теории устойчивости и бифуркаций динамических систем. Теория катастроф изучает зависимость качественного характера решения уравнений от значений параметров этих уравнений. Применительно к САУ на основании теории катастроф можно исследовать, например, потерю устойчивости при постепенном изменении какого-либо параметра, когда возникают бифуркации. Такой пример с исследованием летательного аппарата приводится в [9].

В нелинейных системах возможен режим хаотической динамики, когда траектории систем сильно зависят от начальных условий. Такие режимы возможны в механических системах с зазорами, трением скольжения, нелинейными обратными связями. Основами теории хаоса является так называемое логистическое уравнение и странный аттрактор (внутри которых нельзя предугадать поведение траекторий на длительный интервал). Изучение таких режимов позволяет глубже понять процессы в НСАУ и научно обосновать законы управления ими.

Для глубокого изучения методов современной теории автоматического управления могут быть использованы упомянутые книги.

Литература

1. Теория автоматического управления. Конспект лекций. В 2 ч. Ч. 1: Линейные непрерывные системы: учеб.-метод. пособие / В. П. Кузнецов,
С. В. Лукьянец, М. А. Крупская. – Минск: БГУИР, 2007. – 132 с.

2. Кузнецов, В. П. Линейные непрерывные системы: тексты лекций по курсу «Теория автоматического управления» для студ. спец. «Автоматика и управление в технических системах» / В. П. Кузнецов. – Минск: БГУИР, 1995. – 180 с.

3. Иванов, В. А. Теория дискретных систем автоматического управления. / В. А. Иванов, А. С. Ющенко. – М.: Наука, 1983. – 336 с.

4. Теория автоматического управления в 2 частях. / Под ред. А. А. Воронова. – М.: Высш. шк., 1986. Ч.1 – 362 с. Ч.2. – 382 с.

5. Кузнецов, В. П. Линейные импульсные системы: математическое описание: тексты лекций по курсу «Теория автоматического управления» для студентов специальности «Автоматика и управление в технических системах» / В. П. Кузнецов. – Минск: БГУИР, 1996. – 70 с.

6. Бесекерский, В. А. Теория автоматического управления / В. А. Бесекерский, Е. П. Попов. – СПб.: Профессия, 2004. – 752 с.

7. Попов, Е. П. Теория нелинейных систем автоматического управления/ Е. П. Попов. – М.: Наука, 1979. – 256 с.

8. Теория автоматического управления: учеб. пособие / М. М. Савин, В. С. Елсуков, О. Н. Пятина; под ред. В. И. Лачина. – Ростов н/Д: Феникс, 2007. – 469 с.

9. Методы классической и современной теории автоматического управления: учебник в 5 т. / Под ред. К. А. Пупкова, Н. Д. Егупова. – М.: Изд-во МГТУ, 2004. Т. 5 – 784 с.

Date: 2015-08-06; view: 646; Нарушение авторских прав