
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Влияние маневрирования судна на гирокомпас
|
|
Судно во время плавания может изменять параметры своего движения (курс и скорость), что приводит к появлению ускорений и обусловленных ими сил инерции. В результате чувствительный элемент гирокомпаса подвергается воздействию моментов сил инерции, которые выводят его из положения равновесия. Погрешности, появляющиеся при маневрировании судна вследствие указанных выше причин, называются инерционными.
На работу гирокомпаса типа «Курс» оказывают влияние девиации первого и второго рода.
Инерционная девиация первого рода – это угол, на который отклонится главная ось гиросферы в результате действия сил инерции, вызванных маневрированием, на устройство, превращающее свободный гироскоп в гирокомпас (для ГК «Курс» - на пониженный центр тяжести).
Инерционное перемещение первого рода – это угол, на который отклонится главная ось гиросферы в результате действия сил инерции на устройство, превращающее свободный гироскоп в гирокомпас (на пониженный центр тяжести) за время действия ускорения
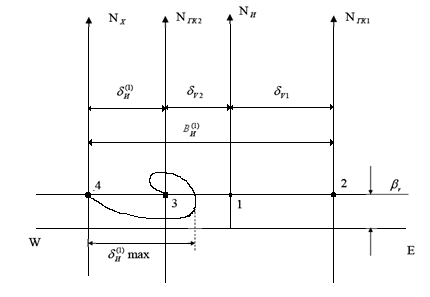
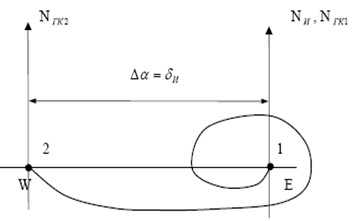
Пример инерционной девиации первого рода и инерционного перемещения первого рода показаны на рисунке ниже:
Как видно из рисунка, связь между инерционной девиацией первого рода и инерционным перемещением первого рода можно представить формулой: 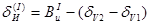 .
.
Используя исходные данные, рассчитаем величину инерционной девиации первого рода у гирокомпаса типа «Курс» на конец маневра:
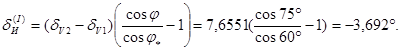
Построим график характера движения чувствительного элемента ГК «Курс» и гирокомпасного меридиана при маневрировании судна для случаев 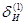 при движении судна с заданными исходными параметрами.
при движении судна с заданными исходными параметрами.
1. Наносим на рисунок плоскость горизонта, истинный меридиан и 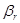 – угол отклонения главной оси гиросферы от плоскости горизонта. Для северной широты главная ось гиросферы приподнята над плоскостью горизонта, а для южной широты – опущена за плоскость горизонта, что видно из формулы
– угол отклонения главной оси гиросферы от плоскости горизонта. Для северной широты главная ось гиросферы приподнята над плоскостью горизонта, а для южной широты – опущена за плоскость горизонта, что видно из формулы 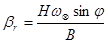 , (для S широт sin φ < 0, значит βr < 0; для N широт sin φ > 0, значит βr > 0).
, (для S широт sin φ < 0, значит βr < 0; для N широт sin φ > 0, значит βr > 0).
2. Определяем положение гиросферы до маневра. Так как, перед маневрированием судно имело какую-то скорость (в нашем случае V 1 = 13 уз), двигаясь ГКК 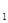 = 1450, то в показаниях гиросферы будет присутствовать скоростная девиация, т.е. главная ось гиросферы будет находиться не в плоскости истинного меридиана (точка 1), а в гирокомпасном меридиане (N
= 1450, то в показаниях гиросферы будет присутствовать скоростная девиация, т.е. главная ось гиросферы будет находиться не в плоскости истинного меридиана (точка 1), а в гирокомпасном меридиане (N 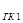 точка 2),положение которого определяется величиной и знаком скоростной девиации (
точка 2),положение которого определяется величиной и знаком скоростной девиации (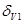 ) до маневра судна. Для нашего примера скоростная девиация до маневра имеет знак плюс. Поэтому главная ось гиросферы будет отклонена к E на угол
) до маневра судна. Для нашего примера скоростная девиация до маневра имеет знак плюс. Поэтому главная ось гиросферы будет отклонена к E на угол 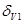 перед маневрированием судна. Т.к.
перед маневрированием судна. Т.к. 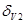 имеет знак минус и
имеет знак минус и 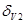 <
< 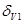 , то новый гирокомпасный меридиан будет отклонен к W на угол, меньший чем в предыдущем случае
, то новый гирокомпасный меридиан будет отклонен к W на угол, меньший чем в предыдущем случае
3. Определяем положение гиросферы, которое она должна занять после окончания маневра. Так как после завершения маневрирования судно изменило параметры своего движения (V 2 = 22 уз, ГКК2 = 0300), главная ось гиросферы должна переместиться в новый гирокомпасный меридиан (N 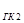 ), т.е. в точке 3.
), т.е. в точке 3.
Однако на конец маневра главная ось гиросферы «обгонит» новый гирокомпасный меридиан (N 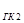 ) и на конец маневра окажется в меридиане N
) и на конец маневра окажется в меридиане N 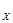 (точка 4). Это происходит вследствие того, что в широте маневрирования ниже расчетной период незатухающих колебаний гирокомпаса будет меньше, чем в расчетной широте (что видно из формулы
(точка 4). Это происходит вследствие того, что в широте маневрирования ниже расчетной период незатухающих колебаний гирокомпаса будет меньше, чем в расчетной широте (что видно из формулы 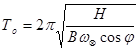 ), соответственно угловая скорость прецессии главной оси гиросферы будет больше угловой скорости движения нового гирокомпасного меридиана (т.к.
), соответственно угловая скорость прецессии главной оси гиросферы будет больше угловой скорости движения нового гирокомпасного меридиана (т.к. 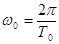 ). Если бы плавание происходило в широте выше расчетной, то наблюдалась бы противоположная ситуация (главная ось гиросферы на конец маневра не дошла бы до нового гирокомпасного меридиана, т.к. угловая скорость прецессии гиросферы была бы меньше угловой скорости движения нового гирокомпасного меридиана). При маневрировании судна в расчетной широте инерционная девиация первого рода будет отсутствовать, и главная ось гиросферы на конец маневра окажется в новом компасном меридиане. Это объясняется тем, что в данной широте соблюдается условие апериодического (бесколебательного) перехода. Для ГК «Курс» расчетная широта равна 60°.
). Если бы плавание происходило в широте выше расчетной, то наблюдалась бы противоположная ситуация (главная ось гиросферы на конец маневра не дошла бы до нового гирокомпасного меридиана, т.к. угловая скорость прецессии гиросферы была бы меньше угловой скорости движения нового гирокомпасного меридиана). При маневрировании судна в расчетной широте инерционная девиация первого рода будет отсутствовать, и главная ось гиросферы на конец маневра окажется в новом компасном меридиане. Это объясняется тем, что в данной широте соблюдается условие апериодического (бесколебательного) перехода. Для ГК «Курс» расчетная широта равна 60°.
Затем, при включении масляного успокоителя,главная ось гиросферы затухающими колебаниями, в плоскость нового гирокомпасного меридиана (N 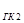 , точка 3). Начальная траектория движения гиросферы пойдет вниз, т.к. на конец маневра главная ось гиросферы оказалась к западу от нового гирокомпасного меридиана. Восточная часть плоскости горизонта в результате суточного вращения Земли опускается. Следовательно, ось гиросферы пойдёт вниз относительно плоскости горизонта.
, точка 3). Начальная траектория движения гиросферы пойдет вниз, т.к. на конец маневра главная ось гиросферы оказалась к западу от нового гирокомпасного меридиана. Восточная часть плоскости горизонта в результате суточного вращения Земли опускается. Следовательно, ось гиросферы пойдёт вниз относительно плоскости горизонта.
Далее на рисунке обозначим углы, характеризующие инерционную девиацию первого рода (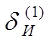 ) и инерционное перемещение первого рода (B
) и инерционное перемещение первого рода (B 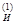 ).
).
Инерционная девиация второго рода – это угол, на который отклоняется главная ось гиросферы при маневрировании судна в результате действия сил инерции на устройство, обеспечивающее демпфирование незатухающих колебаний гиросферы (в ГК «Курс» - на масляный успокоитель).
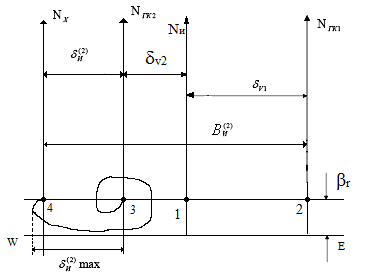
Построим график характера движения главной оси гиросферы и нового гирокомпасного меридиана в случае инерционной девиации 2-ого рода для выше принятых параметров маневрирования. Поскольку в рассматриваемом случае маневрирование происходит не в расчетной широте, то мы будем иметь дело с суммарной инерционной девиацией (т.е. будет присутствовать инерционная девиация и первого, и второго рода). Момент, вызванный пониженным центром тяжести и момент от перетекания жидкости направлены в противоположные стороны, поэтому угловая скорость перемещения главной оси гиросферы будет меньше, чем перемещение плоскости нового гирокомпасного меридиана (ωвкл = (Lм – Lж.у.)/Н). В связи с этим главная ось гиросферы на конец маневра не будет доходить до нового гирокомпасного меридиана независимо от широты маневрирования. Так как плавание происходит в широте ниже расчетной, то  и
и  будут иметь разные знаки, и суммарная инерционная девиация будет частично компенсироваться.
будут иметь разные знаки, и суммарная инерционная девиация будет частично компенсироваться.
В данном случае положение гирокомпасных меридианов будут такими же, как в случае без использования масляного успокоителя, но положение оси гиросферы на конец маневра будет к западу от нового гирокомпасного меридиана (для наглядности положения гирокомпасных меридианов на рисунке изменены). Вследствие того, что избыток в одном из сосудов на конец маневра сохраняется, постепенно убывая, то и момент от этого избытка также будет существовать некоторое время. За счет этого ось гиросферы начнет отходить от нового гирокомпасного меридиана в ту сторону, где она находилась до маневра, а затем затухающими колебаниями приходить в плоскость нового гирокомпасного меридиана. Начальная траектория движения главной оси гиросферы пойдет вниз, т.к. ось гиросферы на конец маневра оказалась в западной части плоскости горизонта (точка 4) относительно нового гирокомпасного меридиана (а западная часть плоскости горизонта поднимается в результате суточного вращения Земли)
Рассмотрим влияние маневрирования на ГАК «Вега». Возникающие во время ускорения воздействуют на индикатор горизонта, который вырабатывает дополнительный сигнал, пропорциональный северной составляющей ускорения. Этот сигнал приведет к появлению дополнительных управляющих моментов, которые будут действовать в течение всего времени влияния ускорения и в результате приведут к отклонению гироскопа от положения равновесия, в котором он находился до начала маневрирования. По окончании влияния ускорения чувствительный элемент, совершая затухающие колебания, начнет возвращаться в прежнее положение равновесия. Возникающие при этом погрешности называются инерционными девиациями.
Используя исходные данные, рассчитаем величину инерционной девиации у гироазимуткомпаса «Вега» по формуле 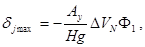
где 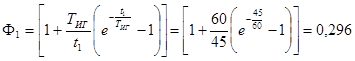 ;
;
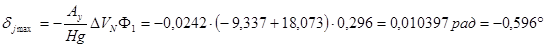
Рассмотрим характер движения чувствительного элемента ГАК «Вега». Широтная и скоростная девиации скомпенсированы корректирующими моментами, следовательно, главная ось гиросферы до маневра будет находиться в плоскости горизонта. В результате маневра судно изменило курс и уменьшило скорость. Согласно заданным параметрам движения инерционная девиация будет со знаком минус, поэтому после маневра главная ось гиросферы будет в западной части плоскости горизонта.
Поскольку данный гирокомпас является корректируемым, и коррекция осуществляется непрерывно, без запаздывания, на основе точной информации о широте и скорости судна, положением главной оси гиросферы после маневра судна будет являться меридиан N 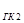 (точка 2). То есть в данном случае инерционное перемещение
(точка 2). То есть в данном случае инерционное перемещение 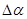 и есть инерционная девиация. Так как главная ось гиросферы под действием горизонтального момента оказалась в западной части плоскости горизонта, которая в результате суточного вращения Земли поднимается, то она получит наклон вниз относительно плоскости горизонта. Момент по вертикальной оси также будет оказывать на гиросферу такое же воздействие. По окончанию маневра, когда исчезнет отклоняющая сила инерции, маятник достаточно быстро возвратится в исходное (вертикальное) положение благодаря суммарному наклону главной оси гиросферы. В этом случае по сигналу ИГ будут формироваться вертикальный и горизонтальный моменты противоположного направления, за счет которых гиросфера затухающими колебаниями возвратится в плоскость меридиана (N
и есть инерционная девиация. Так как главная ось гиросферы под действием горизонтального момента оказалась в западной части плоскости горизонта, которая в результате суточного вращения Земли поднимается, то она получит наклон вниз относительно плоскости горизонта. Момент по вертикальной оси также будет оказывать на гиросферу такое же воздействие. По окончанию маневра, когда исчезнет отклоняющая сила инерции, маятник достаточно быстро возвратится в исходное (вертикальное) положение благодаря суммарному наклону главной оси гиросферы. В этом случае по сигналу ИГ будут формироваться вертикальный и горизонтальный моменты противоположного направления, за счет которых гиросфера затухающими колебаниями возвратится в плоскость меридиана (N  ), то есть в положение до маневра.
), то есть в положение до маневра.
Таким образом, главным отличием в движении главной оси чувствительного элемента у гирокомпасов «Курс» и «Вега» является то, что в ГК «Вега» постоянно поступает информация о широте и скорости судна, вследствие чего устраняются скоростная и широтная девиации на самом ЧЭ (а не в репитерах, как у ГК «Курс»), и главная ось гиросферы до маневра и через некоторое время после него находится в плоскости истинного меридиана. В ГК «Курс» корректирующих моментов нет, поэтому главная ось ЧЭ до маневра находится в одном гирокомпасном меридиане, а после маневра (после погашения инерционной девиации включением масляного успокоителя) переходит в другой гирокомпасный меридиан, и нахождение в плоскости истинного меридиана является редким частным случаем.
2. РАСЧЁТ ПОПРАВКИ ГИРОКОМПАСА
Пусть пелорус гирокомпаса и удалённый ориентир имеют следующие координаты в геодезической системе СК-95 на основе референц – эллипсоида WGS-84:
φp1 = 48º36,025΄N, λp1 = 160º05,881΄W; φop = 48º35,971΄N, λop = 160º04,045΄W
В результате измерений гирокомпасные пеленги удалённого ориентира получили следующие значения:
ГКП1 = 90,1°; ГКП2 = 89,8°; ГКП3 = 90,3°; ГКП4 = 89,9°.
1. Рассчитаем разность долгот в минутах. РД = 1,836΄ (к E).
2. Преобразуем значения широт ориентира и пелоруса в градусную меру делением минут на 60. Получим:
φop = 48º35,971΄N = 48,59951ºN; φp1 = 48º36,025΄N = 48,60041ºN.
3. Рассчитаем значения SI, SII и SIII для широты ориентира, выбирая соответствующие коэффициенты k 1 и k 3 для референц-эллипсоида WGS-84.
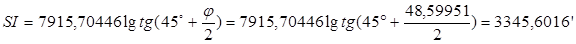 ,
,
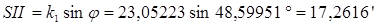 ,
,
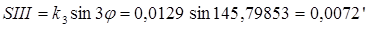 .
.
4. С учётом округления до третьего знака после запятой значение меридиональной части:
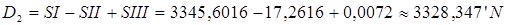 .
.
5. Рассчитаем значения SI, SII и SIII для широты пелоруса, выбирая соответствующие коэффициенты k 1 и k 3 для референц-эллипсоида WGS-84
SI = 3345,6833΄; SII = 17,2918΄; SIII = 0,0073΄.
6. С учётом округления до третьего знака после запятой значение меридиональной части D1 = 3328,340΄ N.
7. Вычислим РМЧ = D 2 – D 1 = 3328,347΄ N – 3328,340΄ N = + 0,007΄ (к N).
8. Рассчитаем К = arctg(РД/РМЧ) = arctg(1,836/0,007) = 89,8° (NE).
Учитывая знаки РД и РМЧ, а также, следуя правилам перехода от четвертного счёта к круговому (если РД > 0 и РМЧ > 0, то Пр = К;), получим Пр = К = 89,8°.
9. Получим осреднённое значение измеренных гирокомпасных пеленгов.
ГКПСР =(90,1° + 89,8° + 90,3° + 89,9°)/4 = 90,025°.
10. Найдём искомую поправку гирокомпаса
ΔГК = Пр – ГКПср = 89,8°– 90,025° = -0,2°.
Расчёт поправки гирокомпаса
| РД | 1,836΄ (к E) | СК - 95 | |
| Ориентир | Пелорус | ||
| φ◦ | 48,59951º N | φ◦ | 48,60041º N |
| SI | 3345,6016΄ | SI | 3345,6833΄ |
| SII | 17,2616΄ | SII | 17,2918΄ |
| SIII | 0,0072΄ | SIII | 0,0073΄ |
| D 2 | 3328,347΄ N | D 1 | 3328,340΄ N |
| РМЧ | + 0,007΄ (к N) | ||
| К | 89,8° (NE) | ПР | 89,8° |
| ГКПСР | 90,025° | ΔГК | -0,2° |
Вывод: так как полученная поправка гирокомпаса по абсолютной величине не превосходит 1°, то меры по её снижению не предпринимаются. Величина этой поправки принимается для дальнейшего использования.
Date: 2015-08-06; view: 1070; Нарушение авторских прав