
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Глава 10. Надежность систем с нагруженным резервированием
|
|
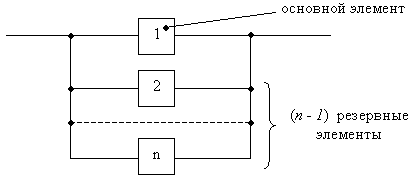
Рассматривается система, состоящая из одного основного и (n - 1) резервных элементов.
При условии, что отказы элементов независимы, отказ системы происходит только при отказе всех n элементов.
Структура системы
Случайная наработка до отказа:
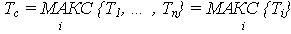
(система работоспособна до тех пор, пока работоспособен хотя бы один элемент).
Поскольку отказ системы есть событие, которое заключается в одновременном появлении событий – отказах всех элементов, то
· вероятность отказа (ВО):
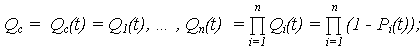
· вероятность безотказной работы (ВБР):
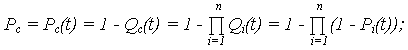
· математическое ожидание (МО) наработки до отказа:
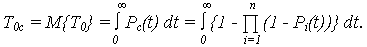
При идентичных элементах системы, т. е. P1(t) = … = Pn(t)
· ВБР:
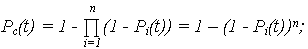
· ВО:
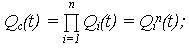
· МО наработки до отказа:
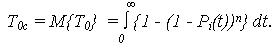
Для системы с экспоненциальной наработкой до отказа каждого из n элементов:
Pi(t) = exp(-  i t),
i t),
где  i = const показатели безотказности:
i = const показатели безотказности:
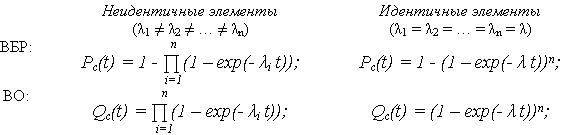
Таким образом, при нагруженном резервировании экспоненциальное распределение наработки до отказа не сохраняется.
При идентичных n элементах системы МО наработки до отказа:
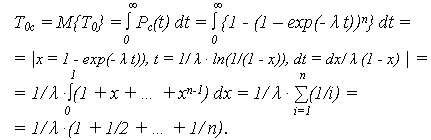
При большом n (n 
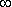 ), T0с
), T0с 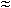 1/
1/  ·(ln n + c), где c = 0.577….
·(ln n + c), где c = 0.577….
При неидентичных элементах:
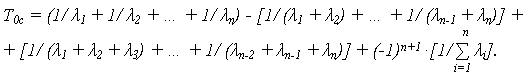
Для системы с n идентичными элементами P1(t) = … = Pn(t) решаются задачи оптимизации (в различных постановках).
1. Определение числа n элементов системы, при котором вероятность отказа (ВО) системы Qс(t) не будет превосходить заданной Qс.
Поскольку Qс(t) = Qin(t), то условие задачи
Qin(t) 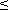 Qс(t).
Qс(t).
Из приведенного неравенства определяется минимально необходимое число элементов:
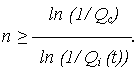
2. Определение надежности n элементов системы из условия, чтобы ВО не превышала заданную Qс.
Из условия Qin(t) 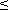 Qс(t), находим ВО I и ВБР Pi(t)
Qс(t), находим ВО I и ВБР Pi(t) 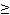 1 - Qi(t).
1 - Qi(t).
Надежность систем с ограничением по нагрузке
Для некоторых систем условия работы таковы, что для работоспособности системы необходимо, чтобы по меньшей мере r элементов из n были работоспособны.
Т. е. число необходимых рабочих элементов – r, резервных – (n - r).
Отказ системы наступает при условии отказа (n – r + 1) элементов.
Если при изменении числа находящихся в работе элементов не наблюдается перегрузки, влияющей на возможность возникновения отказа, то отказы можно считать независимыми.
ВБР такой системы определяется с помощью биномиального распределения.
Для системы, сохраняющей работоспособность при функционировании r из n элементов, ВБР определяется как сумма r, (r + 1), …, (n – r) элементов:
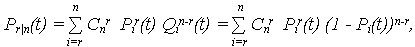
где 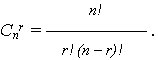
Для идентичных элементов с экспоненциальной наработкой Pi(t) = exp(-  i t),
i t),  i = const (
i = const ( 1 = … =
1 = … =  i = … =
i = … =  n) ВБР:
n) ВБР:
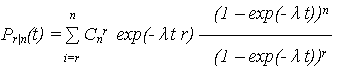
Зависимость надежности системы от кратности резервирования
При целой кратности k (r = 1, n = k + 1) для системы с идентичными элементами и экспоненциальной наработкой до отказа:
· ВБР системы:
Pс(t) = 1 – (1 - exp(-  t))k+1;
t))k+1;
· ПРО системы:
fс(t) = - dPс(t)/ dt = (k + 1)  (1 - exp(-
(1 - exp(-  t))k exp(-
t))k exp(-  t);
t);
· ИО системы:
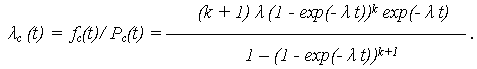
Полагая элементы системы высоконадежными, т. е.  t << 1 (P(t)
t << 1 (P(t) 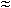 1 -
1 -  t), получены упрощенные выражения:
t), получены упрощенные выражения:
· ВБР системы:
Pс(t) 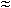 1 – (
1 – ( t))k+1;
t))k+1;
· ПРО системы:
fс(t) 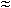 (k + 1)
(k + 1)  k+1 tk;
k+1 tk;
· ИО системы:
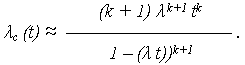
но поскольку  t << 1, то (
t << 1, то ( t)k+1
t)k+1  0, поэтому ИО системы:
0, поэтому ИО системы:
 с (t)
с (t) 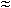 (k + 1)
(k + 1)  k+1 tk = n ·
k+1 tk = n ·  n · tn-1,
n · tn-1,
где n = k + 1.
Полученное выражение  с (t) свидетельствует о том, что при
с (t) свидетельствует о том, что при  = const элементов, ИО системы зависит от наработки, т. е. распределение наработки до отказа системы не подчиняется экспоненциальному распределению.
= const элементов, ИО системы зависит от наработки, т. е. распределение наработки до отказа системы не подчиняется экспоненциальному распределению.
На рис. 1 приведены зависимости изменения Pс( t) и
t) и  с /
с /  (
( t) из которых следует, что:
t) из которых следует, что:
· увеличение кратности резервирования k повышает надежность (Pс возрастает,  с /
с / 
 0);
0);
· резервирование наиболее эффективно на начальном участке работы системы (при t 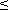 T0), т. е.
T0), т. е.
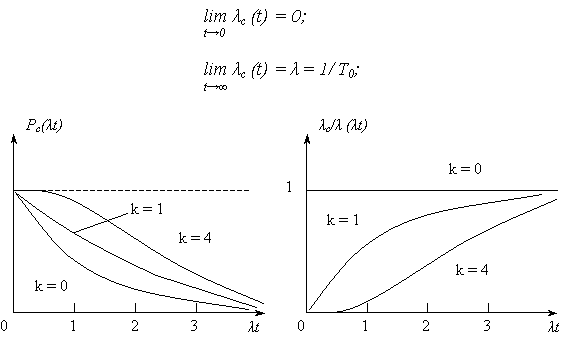
Рис. 10.1
Из графика  с /
с /  (
( t) видно, что при t = (3
t) видно, что при t = (3 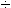 4)T0 = (3
4)T0 = (3 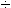 4) 1/
4) 1/  ,
,  с приближается к
с приближается к  .
.
Поскольку средняя наработка до отказа системы при идентичных элементах ( = const):
= const):
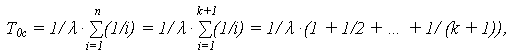
то выигрыш в средней наработке T0с снижается по мере увеличения кратности резервирования.
Например,
при k = 1
T0с = T0 ·(1 + 1/2) = 3/2T0
(увеличение T0с на 50%);
при k = 2
T0с= T0 ·(1 + 1/2 + 1/3) = 11/6T0
(увеличение T0с на 83%);
при k = 3
T0с= 25/12T0
(увеличение T0сна 108%).
Таким образом, динамика роста T0с составляет: 50, 33 и 25%, т. е. уменьшается.
Контрольные вопросы:
1. Чем отличаются системы с нагруженным резервированием с целой и дробной кратностью? Привести расчетные выражения показателей безотказности?
2. Какой закон распределения наработки до отказа будет у системы с нагруженным резервированием, если законы распределения наработки до отказа составляющих ее элементов – экспоненциальные?
3. Какие задачи оптимизации решаются и в чем они состоят для систем с нагруженным резервом?
4. Как определяется вероятность безотказной работы системы с нагруженным резервированием и дробной кратностью?
5. При каких условиях наиболее эффективно применение нагруженного резервирования?
Date: 2015-08-06; view: 524; Нарушение авторских прав