
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Заломлення світла
|
|
53. Світло переходить із повітря у воду. Яка з формул визначає швидкість поширення світла у воді? (a - кут падіння, b - кут заломлення, с – швидкість світла у повітрі).
А) 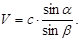 Б)
Б) 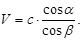 В)
В) 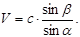 Г)
Г) 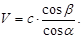 Д)
Д) 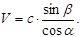
54. Визначити показник заломлення морської води, якщо при куті падіння a =p/4, кут заломлення дорівнює b =30°.
А) 1,41. Б) 1,73. В) 1,33. Г) 1,50. Д) 1,84.
55. Визначити швидкість поширення світла у скипидарі, якщо відомо, що куту падіння 45° відповідає кут заломлення 30°.
А) 2,36×108 м/с. Б) 1,98×108 м/с. В) 2,72×108 м/с. Г) 2,51×108 м/с. Д) 2,12×108 м/с.
56. Визначити абсолютний показник заломлення слюди, якщо при куті падіння світлового пучка 60° кут заломлення дорівнює 30°.
А) 1,33. Б) 2,18. В) 1,41. Г) 1,73 Д) 1,56.
57. Тонкий пучок світла переходить із повітря у рідину із показником заломлення n=1,3. Чому дорівнює кут заломлення b, якщо синус кута падіння дорівнює 0,65?
А) 750. Б) 300. В) 450. Г) 600. Д) 150.
58. При деякому значенні кута падіння променя світла на межу поділу двох прозорих середовищ відношення синуса кута падіння до синуса кута заломлення дорівнює N. Чому дорівнюватиме це відношення при збільшенні кута падіння у 2 рази?
А) 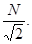 Б)
Б) 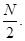 В) 2× N. Г) N. Д)
В) 2× N. Г) N. Д) 
59. Фіолетове світло із довжиною хвилі l0=397 нм падає на прозору пластинку під кутом a =450. Визначте довжину хвилі l цього світла у середовищі, якщо кут заломлення b для цього світла становить 22,90.
А) 184 нм. Б) 321 нм. В) 218 нм. Г) 436 нм. Д) 279 нм.
60. Синє світло із довжиною хвилі 486 нм падає на прозору пластинку під кутом a =450. Визначте довжину хвилі цього світла у середовищі, якщо кут заломлення для цього світла b становить 23,30.
А) 274 нм. Б) 508 нм. В) 326 нм Г) 439 нм. Д) 385 нм.
61. Зелене світло із довжиною хвилі 589 нм падає на прозору пластинку під кутом 600. Визначте довжину хвилі цього світла у середовищі, якщо кут заломлення для цього світла становить 34,60.
А) 494 нм. Б) 623 нм. В) 458 нм. Г) 511 нм. Д) 386 нм.
62. Жовте світло із довжиною хвилі 687 нм падає на прозору пластинку під кутом 600. Визначте довжину хвилі цього світла у середовищі, якщо кут заломлення для цього світла становить 35,90.
А) 536 нм. Б) 465 нм. В) 628 нм. Г) 497 нм. Д) 418 нм.
63. Червоне світло із довжиною хвилі 759 нм падає на прозору пластинку під кутом 750. Визначте довжину хвилі цього світла у середовищі, якщо кут заломлення для цього світла становить 44,20.
А) 548 нм. Б) 706 нм. В) 689 нм. Г) 512 нм. Д) 624 нм.
64. На скляну пластинку із показником заломлення n =1,5 падає промінь світла. Визначте кут падіння променя a, якщо кут g між відбитим та заломленим променями дорівнює 90°?
А) 780. Б) 240. В) 430. Г) 560. Д) 350.
65. Показник заломлення скла дорівнює 1,73. Чому дорівнює кут між відбитим і заломленим променями (у градусах), якщо кут падіння дорівнює 60о?
А) 1200. Б) 300. В) 900. Г) 600. Д) 450.
66. Заломлений промінь утворює з відбитим кут 90°. Визначити показник заломлення речовини, якщо синус кута падіння дорівнює 0,8.
А) 1,33. Б) 2,14. В) 1,41. Г) 1,73. Д) 1,24.
67. Синус кута падіння променя на межу розподілу повітря із прозорим середовищем дорівнює 0,75. Визначте абсолютний показник заломлення цього середовища, якщо кут між відбитим та заломленим променями дорівнює 900.
А) 1,41. Б) 1,13. В) 1,84. Г) 1,50. Д) 1,73.
68. Під яким кутом a повинен упасти промінь на скло із показником заломлення 1,6, щоб відбитий промінь виявився перпендикулярним до заломленого?
А) 460. Б) 290. В) 580. Г) 370. Д) 740.
69. Світловий промінь падає під кутом a на прозоре тіло із показником заломлення n. Визначте зв¢язок між цими величинами, щоб відбитий промінь виявився перпендикулярним до заломленого.
А) tga=n. Б) 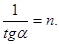 В)
В) 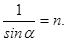 Г) sina=n. Д)
Г) sina=n. Д) 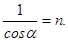
70. Показник заломлення скла дорівнює 1,52. Визначте граничний кут a0 повного внутрішнього відбивання для поверхні розділу скло-повітря.
А) 35,40. Б) 52,60. В) 28,30 Г) 41,10. Д) 23,90.
71. Граничний кут повного внутрішнього відбивання a0 для деякої речовини відносно повітря дорівнює 30°. Знайти показник заломлення n цієї речовини.
А) 1,25. Б) 2,0. В) 1,5. Г) 1,75. Д) 2,25.
72. Коли світловий промінь переходить із алмазу у повітря, граничний кут падіння a0 =24,5°. Обчислити показник заломлення алмазу n.
А) 1,73. Б) 2,02. В) 1,46. Г) 2,41. Д) 2,28.
73. Показник заломлення деякого сорту скла для червоного світла дорівнює 1,51. Визначте граничний кут повного внутрішнього відбивання при падінні цього світла на межу скло-повітря.
А) 41,50. Б) 37,60. В) 28,20. Г) 46,30. Д) 32,80.
74. Показник заломлення деякого сорту скла для фіолетового світла дорівнює 1,65. Визначте граничний кут повного внутрішнього відбивання при падінні цього світла на межу скло-повітря.
А) 43,40. Б) 29,60. В) 40,80 Г) 33,20. Д) 37,30.
75. Який граничний кут при падінні променя на межу скло-вода? Показники заломлення води nв =1,33; скла nс =1,52.
А) 720. Б) 540. В) 470. Г) 610. Д) 390.
76. Промінь світла виходить зі скипидару у повітря. Граничний кут падіння, при якому спостерігається явище повного відбивання, для цього променя дорівнює 42,4°. Визначити швидкість поширення світла у скипидарі.
А) 2,3×108 м/с. Б) 1,7×108 м/с. В) 2,0×108 м/с. Г) 2,7×108 м/с. Д) 2,5×108 м/с.
77. Визначте граничний кут повного внутрішнього відбивання для поверхні розділу вода-повітря. Показник заломлення води дорівнює 1,33.
А) 48,80. Б) 37,60. В) 54,20. Г) 43,40. Д) 34,70.
78. Визначити, під яким кутом j до поверхні водоймища водолаз із-під неї бачить Сонце, яке заходить за горизонт. Показник заломлення води дорівнює 1,33.
А) 36,60. Б) 41,20. В) 28,40. Г) 47,10. Д) 31,80.
79. На заповнену водою склянку покладена скляна пластинка. Під яким кутом a мусить падати на неї світловий промінь, щоб від поверхні розподілу води зі склом відбулось повне внутрішнє відбивання? Показники заломлення скла 1,5, а води 1,33.
А) 64,80. Б) 41,20. В) 72,40. Г) 56,70. Д) Умова не здійснювана.
80. На дно посудини, наповненої водою до висоти 10 см, приміщене точкове джерело світла. Точно над ним на поверхні води плаває кругла непрозора пластинка. Який найменший радіус мусить мати ця пластинка, щоб ні один промінь світла від джерела не зміг вийти через поверхню води?
А) 11,4 см. Б) 9,7 см. В) 5,6 см. Г) 14,2 см. Д) 7,8 см.
81. Вузький паралельний пучок світла падає на плоско паралельну скляну пластинку під кутом a, синус якого дорівнює 0,8. Пучок, який вийшов з пластинки, виявився зсунутим відносно продовження падаючого пучка на відстань 2 см. Яка товщина пластинки d, якщо показник заломлення скла 1,7?
А) 3,4 см. Б) 5,1 см. В) 2,6 см. Г) 4,2 см. Д) 1,8 см.
82. Світловий промінь падає на плоско паралельну скляну пластинку під кутом 300 і виходить з неї паралельно початковому променю. Визначте товщину цієї пластинки d, якщо відстань між променями D становить 1,94 см, а показник заломлення скла 1,5.
А) 7,5 см. Б) 12,5 см. В) 5,0 см. Г) 2,5 см. Д) 10 см.
83. На скляну пластинку (n=1,73) товщиною 1 см падає промінь світла під кутом 600. Частина світла відбивається від верхньої поверхні, а частина, заломлюючись, проходить у скло і відбивається від нижньої поверхні пластинки. Цей промінь, заломившись повторно на верхній поверхні, виходить назад у повітря паралельно першому відбитому променю. Визначити відстань між обома цими променями.
А) 4,6 мм. Б) 7,2 мм. В) 5,8 мм. Г) 6,7 мм. Д) 8,3 мм.
84. Монохроматичне промінь падає нормально на бокову поверхню призми, заломлюючий кут якої J =400. Показник заломлення матеріалу призми для цього променя 1,5. Визначити кут j відхилення променя після виходу із призми від початкового напрямку.
А) 51,90. Б) 34,60. В) 42,80. Г) 17,30. Д) 69,20.
85. Монохроматичний промінь падає нормально на бокову поверхню призми і виходить з неї відхиленим на кут j=250. Показник заломлення матеріалу призми для цього променя n =1,7. Визначити заломлюючий кут призми J.
А) 490. Б) 210. В) 420. Г) 280. Д) 350.
86. Заломлюючий кут рівнобедреної призми J =100. Монохроматичний промінь падає на її бокову грань під кутом a =100. Визначте кут відхилення променя від початкового напрямку, якщо показник заломлення матеріалу призми n =1,6.
А) 60. Б) 220. В) 280. Г) 100. Д) 160.
87. Показник заломлення матеріалу призми для деякого монохроматичного променя світла n =1,6. Визначте максимальний кут падіння a1 цього променя на призму, щоб при виході променя із неї спостерігалось повне внутрішнє відбивання (a 2=900). Заломлюючий кут призми (кут при її вершині J =450).
А) 8,70. Б) 13,40. В) 10,10. Г) 21,80. Д) 18,60.
88. Пучок світла ковзає вздовж бокової грані рівнобедреної призми (a 1=900). Визначте заломлюючий кут призми J (кут при її вершині), щоб заломлений промінь здійснив повне внутрішнє відбивання на іншій боковій грані (a 2=900). Показник заломлення матеріалу призми для цього променя світла n =1,6.
А) 56,70. Б) 83,20. В) 68,60. Г) 45,80. Д) 77,40.
Лінзи
89. Визначте фокусну відстань двоопуклої лінзи, радіуси кривини якої R1=15 см, R2= =-25 см. Показник заломлення матеріалу лінзи n=1,5.
А) 32,5 см. Б) 13,6 см. В) 24,7 см. Г) 18,8 см. Д) 11,4 см.
90. Визначте фокусну відстань плоско-опуклої лінзи, радіуси кривини якої R1=15 см, R2=¥. Показник заломлення матеріалу лінзи n=1,5.
А) 25 см. Б) 30 см. В) 15 см. Г) 20 см. Д) 35 см.
91. Визначте фокусну відстань ввігнуто-опуклої лінзи (позитивний меніск), радіуси кривини якої R1=15 см, R2=25 см. Показник заломлення матеріалу лінзи n=1,5.
А) 75 см. Б) 45 см. В) 90 см. Г) 35 см. Д) 60 см.
92. Визначте фокусну відстань двовгнутої лінзи, радіуси кривини якої R1=-15 см, R2=25 см. Показник заломлення матеріалу лінзи n=1,5.
А) –32,5 см. Б) –9,4 см. В) -24, 7 см. Г) -13,2 см. Д) -18,8 см.
93. Визначте фокусну відстань плоско-вгнутої лінзи, радіуси кривини якої R1=¥, R2= =-15 см. Показник заломлення матеріалу лінзи n=1,5.
А) -35 см. Б) -20 см. В) –15 см. Г) -30 см. Д) -25 см.
94. Визначте фокусну відстань опукло-вгнутої лінзи (негативний меніск), радіуси кривини якої R1=25 см, R2=15 см. Показник заломлення матеріалу лінзи n=1,5.
А) -45 см. Б) -90 см. В) -75 см. Г) -60 см. Д) –30 см.
95. Визначте фокусну відстань кварцової лінзи для ультрафіолетової лінії спектра ртуті (l=259 нм), якщо фокусна відстань для жовтої лінії натрію (l=589 нм) дорівнює 16 см, а показники заломлення кварцу для цих довжин хвилі відповідно 1,504 та 1,458.
А) 17,6 см. Б) 14,5 см. В) 23,4 см. Г) 11,2 см. Д) 20,4 см.
96. Дві однакові двоопуклі лінзи виготовлені з різного скла, показники заломлення якого відповідно дорівнюють 1,5 та 1,7. Чому дорівнює відношення їхніх фокусних відстаней F1/F2.
А) 2,2. Б) 1,1. В) 1,8. Г) 2,7 Д) 1,4.
97. Радіуси кривини поверхонь двоопуклої лінзи R1=R2=50 см. Показник заломлення матеріалу лінзи n=1,5. Визначте оптичну силу цієї лінзи.
А) 2,25 дптр. Б) 1,5 дптр. В) 1,25 дптр. Г) 2,0 дптр. Д) 1,75 дптр.
98. На відстані 15 см від двоопуклої лінзи, оптична сила якої дорівнює 10 дптр, поставили перпендикулярно оптичній осі предмет висотою 2 см. Визначте відстань від лінзи до його зображення.
А) 30 см. Б) 15 см. В) 20 см. Г) 35 см. Д) 25 см.
99. За умов попередньої задачі визначте висоту зображення предмета у лінзі.
А) 3,0 см. Б) 3,5 см. В) 4,0 см. Г) 2,5 см. Д) 5,0 см.
100. Показник заломлення матеріалу двоопуклої лінзи із однаковими радіусами кривини її поверхонь R дорівнює 1,5. Визначте її фокусну відстань F.
А) F=1,5R. Б) F=R. В) F=0,5R. Г) F=2R. Д) F=0,75R.
101. Лінза із фокусною відстанню F=16 см дає різке зображення предмета у двох положеннях, відстань між якими D=60 см. Визначте відстань від предмета до екрана (d+f).
А) 175 см. Б) 200 см. В) 125 см. Г) 100 см. Д) 150 см.
102. Двоопукла лінза, обмежена двома сферичними поверхнями однакового радіуса кривини 12 см, розташована на такій відстані від предмета, що його збільшення Г=1. Показник заломлення матеріалу лінзи n=1,5. Визначте відстань від предмета до екрана (d+f).
А) 36 см. Б) 60 см. В) 24 см. Г) 48 см. Д) 12 см.
103. Визначте відстань від предмета до екрана (d+f) за умов попередньої задачі, як-що збільшення предмета Г=20.
А) 1,85 м. Б) 1,45 м. В) 2,65 м. Г) 1,15 м. Д) 2,25 м.
104. Визначте відстань від предмета до екрана (d+f) за умов попередньої задачі, як-що збільшення предмета Г=0,2.
А) 86,4 см. Б) 62,5 см. В) 49,4 см. Г) 98,8 см. Д) 74,2 см.
105. Двоопукла лінза, обмежена двома сферичними поверхнями однакового радіуса кривини 12 см, занурена у воду. Показник заломлення матеріалу лінзи n1=1,5, а води n2=1,33. Визначте фокусну відстань цієї лінзи.
А) 31 см. Б) 47 см. В) 24 см. Г) 38 см. Д) 56 см.
106. Визначте фокусну відстань лінзи за умов попередньої задачі, якщо вона занурена у сірковуглець, показник заломлення якого n2=1,63.
А) -90 см. Б) -45 см. В) -30 см. Г) -75 см. Д) -60 см.
107. Визначте фокусну відстань лінзи зануреної у воду F2, якщо її фокусна відстань у повітрі F1=20 см. Показник заломлення матеріалу лінзи n1=1,6, а води n2=1,33.
А) 33 см. Б) 51 см. В) 67 см. Г) 42 см. Д) 59 см.
108. Яка оптична сила лінзи, фокусна відстань якої 100 мм?
А) 1 дптр. Б) 10 дптр. В) 100 дптр. Г) 0,1 дптр. Д) 0,01 дптр.
109. Визначте оптичну силу лінзи, фокусна відстань якої дорівнює 250 см.
А) 0,4 дптр. Б) 1,6 дптр. В) 0,2 дптр. Г) 2,4 дптр. Д) 0,8 дптр.
110. Оптична сила лінзи 25 діоптрій. Визначити у сантиметрах її фокусну відстань.
А) 2 см. Б) 16 см. В) 8 см. Г) 24 см. Д) 4 см.
111. Головна фокусна відстань збірної лінзи 25 см. Предмет знаходиться на відстані 75 см від лінзи. Яким вийде зображення предмета - збільшеним чи зменшеним, дійсним чи уявним, прямим чи перевернутим?
| А) зменшеним, уявним, перевернутим | Б) збільшеним, дійсним, перевернутим | В) зменшеним, дійсним, перевернутим | Г) збільшеним, уявним, перевернутим | Д) зменшеним, дійсним, прямим. |
112. Головна фокусна відстань збірної лінзи 20 см. Предмет знаходиться на відстані 25 см від лінзи. Яким вийде зображення предмета - збільшеним чи зменшеним, дійсним чи уявним, прямим чи перевернутим?
| А) збільшеним, уявним, перевернутим | Б) зменшеним, дійсним, перевернутим | В) зменшеним, дійсним, прямим. | Г) збільшеним, дійсним, перевернутим | Д) зменшеним, уявним, перевернутим. |
113. Головна фокусна відстань збірної лінзи 20 см. Предмет знаходиться на відстані 50 см від лінзи. Яким вийде зображення предмета - збільшеним чи зменшеним, дійсним чи уявним, прямим чи перевернутим?
| А) зменшеним, дійсним, перевернутим | Б) збільшеним, дійсним, перевернутим | В) зменшеним, уявним, перевернутим | Г) зменшеним, дійсним, прямим. | Д) збільшеним, уявним, перевернутим. |
114. Головна фокусна відстань об'єктива проекційного апарату F =12 см. Діапозитив розташований на відстані d =12,5 см від об'єктива. Визначте лінійне збільшення Г цього апарату.
А) 96. Б) 24. В) 72. Г) 36. Д) 48.
115. Головна фокусна відстань розсіюючої лінзи F =50 см. Зображення предмета отримали у 40 см від лінзи. Чому дорівнює відстань d від предмета до лінзи?
А) 240 см. Б) 120 см. В) 200 см. Г) 80 см. Д) 160 см.
116. Яким буде зображення предмета за умов попередньої задачі – збільшеним чи зменшеним, дійсним чи уявним, прямим чи перевернутим?
| А) зменшеним, уявним, перевернутим | Б) зменшеним, дійсним, прямим. | В) зменшеним, дійсним, перевернутим | Г) збільшеним, уявним, перевернутим | Д) зменшеним, уявним, прямим. |
117. Свічка горить на відстані 2 м від стіни. Між стіною та свічкою на відстані 0,4 м від свічки розмістили збірну лінзу, так що на стіні отримали чітке зображення свічки. Визначити фокусну відстань лінзи F.
А) 96 см. Б) 32 см. В) 48 см. Г) 64 см. Д) 24 см.
118. За допомогою двоопуклої лінзи з фокусною відстанню 5 см розглядають монету діаметром 1 см і одержують її уявне зображення діаметром 4 см. На якій відстані d від лінзи знаходиться монета?
А) 5,75 см. Б) 4,5 см. В) 5,25 см. Г) 6,25 см. Д) 6,75 см.
119. На якій відстані від збірної лінзи із фокусною відстанню 30 см буде зображення, якщо предмет помістити на відстані 10 см від лінзи?
А) –15 см. Б) -30 см. В) –25 см. Г) –20 см. Д) –35 см.
120. Яким буде зображення предмета за умов попередньої задачі - збільшеним чи зменшеним, дійсним чи уявним, прямим чи перевернутим?
| А) збільшеним, уявним, перевернутим | Б) збільшеним, дійсним, прямим. | В) збільшеним, уявним, прямим. | Г) зменшеним, уявним, прямим. | Д) збільшеним, дійсним, перевернутим |
121. Чому дорівнює фокусна відстань лінзи, якщо для отримання дійсного зображення предмета у натуральну величину предмет помістили на відстані 30 см від лінзи?
А) 30,0 см. Б) 7,5 см. В) 45 см. Г) 60 см. Д) 15 см.
122. На якій відстані від збірної лінзи з фокусною відстанню 20 см буде зображення, якщо предмет помістити на відстані 4 см від лінзи?
А) –25 см. Б) –10 см. В) –5 см. Г) –20 см. Д) –15 см.
123. Яким буде зображення предмета за умов попередньої задачі - збільшеним чи зменшеним, дійсним чи уявним, прямим чи перевернутим?
| А) збільшеним, уявним, прямим. | Б) збільшеним, дійсним, перевернутим | В) збільшеним, уявним, перевернутим | Г) зменшеним, уявним, прямим. | Д) збільшеним, дійсним, прямим. |
124. Чому дорівнює збільшення зображення Г у збірній лінзі, якщо відстань предмету від лінзи d=12 см, а головна фокусна відстань лінзи дорівнює F=8 см?
А) 4,0. Б) 1,5. В) 3,2. Г) 2,0. Д) 0,5.
125. Чому дорівнює збільшення у збірній лінзі, якщо відстань предмета від лінзи d=1,5×F? (F – фокусна відстань лінзи).
А) 0,5. Б) 2,0. В) 1,5. Г) 4,0. Д) 3,2.
126. Яка має бути відстань d предмету від збірної лінзи, головна фокусна відcтань якої F=10 см, якщо треба отримати збільшення Г=2?
А) 5 см. Б) 10 см. В) 25 см. Г) 20 см. Д) 15 см.
127. Виразити лінійне збільшення Г збірної лінзи, якщо фокусна відстань лінзи F=16 см, а відстань предмета від лінзи d=24 см?
А) 3,2. Б) 1,5. В) 2,0. Г) 0,5. Д) 4,0.
128. Відстань від предмета до збірної лінзи у 5 разів більша, ніж фокусна відстань лінзи. У скільки разів зображення предмету буде меншим, ніж сам предмет?
А) У 6 разів. Б) У 3 рази. В) У 0,5 разів. Г) У 4 рази. Д) У 2 рази.
129. Предмет висотою 30 см розташований вертикально на відстані 80 см від збірної лінзи з оптичною силою 5 дптр. Визначити висоту його зображення.
А) 15 см. Б) 10 см. В) 25 см. Г) 5 см. Д) 20 см.
130. Визначте фокусну відстань лінзи, якщо при відстані 40 см від лінзи до предмета його дійсне зображення знаходиться на відстані 2 м від лінзи.
А) 72 см. Б) 24 см. В) 50 см. Г) 61 см. Д) 33 см.
131. Предмет висотою 20 см розташований вертикально на відстані 60 см від лінзи з оптичною силою 3 дптр. Визначити висоту його зображення.
А) 10 см. Б) 5 см. В) 25 см. Г) 15 см. Д) 20 см.
132. Визначте лінійне збільшення Г у тонкій збірній лінзі, якщо фокусна відстань лінзи дорівнює F, а відстань від лінзи до предмета становить d.
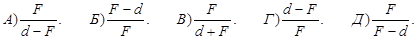
133. Визначте лінійне збільшення Г у тонкій збірній лінзі, якщо фокусна відстань лінзи дорівнює F, а відстань від лінзи до предмета становить n×F.
А) n×F. Б) 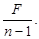 В) (n+1)×F. Г)
В) (n+1)×F. Г)  Д) (n-1)×F.
Д) (n-1)×F.
134. Якою мусить бути відстань d від предмета до збірної лінзи, якщо фокусна відстань лінзи дорівнює F, а її лінійне збільшення становить Г?
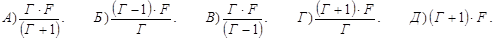
135. Відстань d від предмета до збірної лінзи у 5 разів більша, ніж фокусна відстань лінзи F. У скільки разів зображення предмету h¢ буде меншим за сам предмет h?
А) У 4 рази. Б) У 8 разів. В) У 5 разів. Г) У 10 разів. Д) У 2 рази.
136. Лінза зі скла із показником заломлення n1=1,7 має у повітрі фокусну відстань 16 см. Визначити її фокусну відстань у скипидарі, показник заломлення якого n2= =1,48.
А) 60 см. Б) 90 см. В) 45 см. Г) 30 см. Д) 75 см.
137. Плоско-опукла лінза із радіусом кривини 30 см і показником заломлення 1,5 дає зображення предмета зі збільшенням Г =2. Визначте відстань d від лінзи до предмета.
А) –60 см. Б) –45 см. В) -90 см. Г) –75 см. Д) –30 см.
138. За умов попередньої задачі визначте відстань f від лінзи до зображення предмета.
А) 135 см. Б) 180 см. В) 45 см. Г) 90 см. Д) 150 см.
139. Визначте поздовжню хроматичну аберацію DF=(F1-F2) двоопуклої лінзи із флінтгласу з однаковими радіусами кривини R1=R2 =8 см. Показники заломлення флінтгласу для червоного та фіолетового світла відповідно дорівнюють 1,5 та 1,8.
А) 4 см. Б) 2 см. В) 5 см. Г) 3 см. Д) 1 см.
140. На відстані 40 см перед лінзою за умов попередньої задачі на оптичній осі знаходиться світна точка, яка випромінює червоне світло із довжиною хвилі 760 нм. Визначте відстань f від лінзи до зображення цієї точки.
А) 20 см. Б) 15 см. В) 30 см. Г) 25 см. Д) 10 см.
141. За умов попередньої задачі визначте відстань f від лінзи до зображення світної точки, яка випромінює фіолетове світло із довжиною хвилі 430 нм.
А) 5,7 см. Б) 10,2 см. В) 7,4 см. Г) 4,3 см. Д) 12,6 см.
142. Визначте збільшення, яке дає лупа, фокусна відстань якої F =2 см, для нормального ока із відстанню найкращого зору L =25 см.
А) 7,5. Б) 15,0. В) 12,5. Г) 10,0. Д) 5,0.
143. Визначте збільшення, яке дає лупа, фокусна відстань якої F =2 см, для коротко-зорого ока із відстанню найкращого зору L =15 см.
А) 10,0. Б) 2,5. В) 5,0. Г) 7,5. Д) 12,5.
144. Визначте радіуси кривини, що обмежують лупу (R1=R2), щоб вона давала збільшення для нормального ока Г=10. Відстань нормального зору L=25 см, а показник заломлення скла лінзи n=1,5.
А) 7,5 см. Б) 2,5 см. В) 10 см. Г) 5,0 см. Д) 12,5 см.
145. Мікроскоп складається з об¢єктиву із фокусною відстанню F1=2 мм та окуляра із фокусною відстанню F2=40 мм. Відстань між їхніми фокусами дорівнює 18 см. Визначте збільшення Г, яке дає мікроскоп. Відстань нормального зору L=25 см.
А) 281. Б) 456. В) 618. Г) 374. Д) 562.
146. На якій відстані d від збірної лінзи із фокусною відстанню F=12 см потрібно поставити предмет, щоб його дійсне зображення виявилось втричі більшим за сам предмет?
А) 16 см. Б) 24 см. В) 48 см. Г) 12 см. Д) 32 см.
147. Відстань між предметом і екраном дорівнює 3 м. На якій відстані від предмета d треба примістити збірну лінзу, щоб отримати на екрані чітке зображення предмета, збільшене у 5 разів?
А) 150 см. Б) 75 см. В) 50 см. Г) 125 см. Д) 25 см.
148. На якій відстані d від збірної лінзи із фокусною відстанню F потрібно розмістити предмет, щоб відстань від предмета до його дійсного зображення (d+f) було мінімальним?
А) dmin=F/2. Б) dmin=5F/2. В) dmin=F/2. Г) dmin=2F. Д) dmin=3F/2.
ОСНОВИ ТЕОРІЇ ІЗ РОЗДІЛУ “Хвильова оптика”
Хвильова оптика вивчає сукупність явищ, у яких виявляється хвильова природа світла. З хвильової точки зору, під світлом розуміють електромагнітне випромінювання, сприймане людським оком. Діапазон довжин хвиль видимого світла лежить в межах (4¸8)×10-7 м. До світлових хвиль відносять також невидиме для ока електромагнітне випромінювання: інфрачервоне (ІЧ) випромінювання в діапазоні 5×10-4¸8×10-7 м, і ультрафіолетове (УФ) випромінювання в діапазоні 4×10-7¸10-9 м. Це пов'язано з тим, що властивості ІЧ та УФ електромагнітних хвиль близькі до властивостей видимого світла.
У основі хвильової оптики лежить принцип Гюйгенса: кожна точка середовища, якої досягає хвиля, служить центром вторинних хвиль, а обвідна цих хвиль дає положення хвильового фронту у наступний момент часу (хвильовий фронт – геометричне місце точок простору, до яких доходять світлові коливання до певного моменту часу). Він може пояснити закони відбивання і заломлення світла.
Інтерференцією світла називається накладання двох або декількох світлових хвиль, в результаті якого відбувається просторовий перерозподіл енергії цих хвиль і виникає інтерференційна картина – світлі і темні ділянки, які чергуються між собою (максимуми і мінімуми інтенсивності світла). Необхідною умовою інтерференції хвиль є їхня когерентність: хвилі повинні бути монохроматичними (мати однакову частоту коливань) і сталу у часі різницю фаз D j цих коливань. При цьому різниця фаз когерентних коливань, які накладаються, визначатиметься різницею ходу
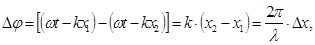
| світлових хвиль: де Dх=(х2-х1) називається геометричною різницею ходу двох хвиль. Якщо в точку |
спостереження обидві світлові хвилі приходять синфазно (фази їх коливань однакові або відрізняються на парне число p), то в цій точці світлові коливання підсилюють одне одного. Іншими словами, якщо Dj=±2kp (де k=0,1,2,…), при цьому Dх=±k×l (тобто на різниці ходу хвиль укладається ціле число довжин хвиль або парне число півхвиль), це є умовою інтерференційного максимуму. Якщо ж світлові хвилі в точку спостереження приходять у протилежних фазах (фази коливань відрізняються на непарне число p), то в цій точці світлові коливання ослабляють одне одного. Або ж, якщо Dj=±(2k+1)p, то при цьому Dх=±(2k+1)×l/2 (тобто на різниці ходу хвиль укладається пів ціле число довжин хвиль або непарне число півхвиль), це є умовою інтерференційного мінімуму.
Розглянутий спосіб отримання інтерференційної картини називається методом Юнга. У ньому когерентними джерелами світла служать дві вузькі щілини S1 і S2, розташовані поблизу одна до одної на відстані d, які є реальними або уявними зображеннями єдиного джерела світла у будь-якій оптичній системі. Результат інтерференції спостерігається на екрані, розташованому паралельно обом щілинам на великій відстані l від них. Початок відліку картини вибраний у точці О, симетричній щодо обох щілин. Інтенсивність картини у будь-якій точці А екрану, лежачої на відстані х від точки О, визначається різницею ходу світлових хвиль від обох джерел D=S2-S1. Неважко показати, що в даному випадку D=x×d/l (при l>>d), звідки легко одержати вирази для координат інтерференційних максимумів і мінімумів:
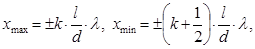
| де k =0,1,2,…- порядок максимумів і мінімумів. Головний максимум, відповідний k =0 знаходитиметься у точці О, а по обидві сторони від ньо- |
го на рівних відстанях будуть розташовані максимуми і мінімуми першого, другого і т. д. порядків, які чергуються між собою. Відстань Dх між сусідніми максимумами
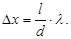
| або мінімумами називається шириною інтерференційної смуги, рівною у даному випадку: Описана картина справедлива лише для монохроматичного світла. |
При відбиванні світла від верхньої і нижньої поверхонь тонкої прозорої плоско-паралельної пластинки, можливі два види інтерференційних картин.
1) Смуги рівного нахилу – інтерференційні смуги, що виникають в результаті накладання проміння, падаючого на плоско-паралельну пластинку розсіяним пучком (під різними кутами).
2) Смуги рівної товщини - інтерференційні смуги, що виникають в результаті накладення паралельного пучка проміння, відображеного від пластинки змінної товщини (клиноподібної).
Результат накладання когерентного проміння визначається оптичною різницею
| D =n1×S1-n2×S2, | ходу D між ними: де S1 і S2 – геометричні довжини шляхів, які проходять обидва про-мені в різних середовищах, n1 та n2 – показники заломлення цих се- |
редовищ. Оптична різниця ходу при відбиванні променя світла від прозорої пластин-
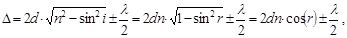
| ки завтовшки d становить: де i - кут падіння променя на пластинку, r – кут заломлення променя. Поява |
доданку ±l/2 обумовлена втратою півхвилі при відбиванні променя світла від верх-
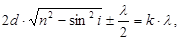
| ньої поверхні пластинки. У відбитому світлі умова інтерференційних максимумів має вигляд: |
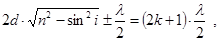
| Умова інтерференційних мінімумів має вигляд: де k =0,1,2,… - порядок інтерференції. У проходячому |
світлі умови посилення та ослаблення міняються місцями.
Типовим прикладом смуг рівної товщини є кільця Ньютона – інтерференційна картина, спостережувана при відбиванні світла від повітряного зазору змінної товщини, утвореного між плоско-паралельною пластинкою та стичною із нею плоско-
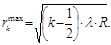
| опуклою лінзою із великим радіусом кривини R. У відбитому світлі радіус к-того світлого кільця обчислюється так: |
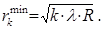
| Для обчислення радіусу к-того темного кільця маємо: У проходячому світлі темні і світлі кільця міняються місцями. |
Дифракцією називається явище відхилення світла від його прямолінійного по-ширення, внаслідок чого світлові хвилі можуть потрапляти у зону геометричної тіні, проникаючи через малі отвори, або огинати непрозорі перешкоди. Це явище є загальним для всіх хвильових процесів, але для світла має особливості, оскільки довжини світлових хвиль l набагато менша розмірів d перешкод або отворів. Тому спостерігати дифракцію можна тільки на досить великих відстанях l від перешкоди (l³d2/l).
Дифракція Френеля (у збіжних пучках) – це дифракція сферичних світлових хвиль, спостережувана на кінцевій відстані від перешкоди – малого круглого отвору або малого круглого диска. Дифракційна картина є світлими і темними кільцями, що чергуються, центри яких знаходяться в центрі перешкоди. Чи буде в центрі світла або темна пляма при дифракції на отворі залежить від діаметру отвору. При дифракції на диску в центрі завжди спостерігається максимум (пляма Пуассона).
Дифракція Фраунгофера (у паралельних променях) - це дифракція плоских світлових хвиль, коли і джерело світла, і точка спостереження нескінченно віддалені від перешкоди, що викликала дифракцію. Практично для її спостереження потрібно точкове джерело світла помістити у фокусі збірної лінзи, а дифракційну картину спостерігати у фокальній площині іншої збірної лінзи, встановленої за перешкодою. У цьому випадку плоска світлова хвиля падає нормально площині щілини шириною а. Паралельні пучки проміння, що виходять із неї у довільному напрямку j (j називають кутом дифракції), збираються лінзою у деякій точці В. Різниця ходу світлових хвиль D від крайніх точок хвильового фронту становить D =а×sinj. Умова дифрак -
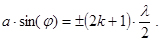
| ційного максимуму у точці спостереження В (якщо на різниці ходу укладається непарне число зон Френеля) має вигляд: Умова дифракційного мінімуму (якщо на різниці ходу укла- |
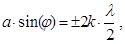
| дається парне число зон Френеля) має вигляд: де k= 1, 2, 3, … - порядок дифракційних мінімумів. |
Система паралельних щілин (штрихів) рівної товщини, розташованих у одній площині і розділених рівними по ширині непрозорими проміжками, називається дифракційними гратами. Відстань між сусідніми щілинами d (сумарна ширина щілини а і непрозорого проміжку b) називається сталою (або періодом) дифракційних грат (d=a+b). Дифракційна картина на гратах є результатом взаємної інтерференції світлових хвиль, що ідуть з усіх щілин, тобто здійснюється багато променева інтерференція когерентних дифрагованих пучків світла. Різниця ходу світлових хвиль від відповідних точок хвильових фронтів, що потрапляють до сусідніх щілин, становить
| d×sinj=±k×l, | D =d×sinj. При кутах дифракції, які задовольняють умові: відповідні вторинні світлові хвилі накладатимуться у однакових фазах і даватимуть головні максимуми інтенсивності. |
Якщо грати містять N штрихів, то d=1/N. Роздільна здатність дифракційних грат
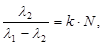
| визначається співвідношенням: де l1 та l2 – довжини хвиль двох близьких спектральних ліній, які іще розділяються гратами, N – загальна кількість щілин грат, k – |
порядок дифракційного спектру. Очевидно, що чим більше N, тим більш близькі довжини хвиль можуть бути розділені.
Для спостереження дифракції рентгенівського випромінювання (l» 10-8¸10-12 м) можуть бути використані кристали, відстані між атомами в яких d» 10-10 м. Пучок монохроматичного рентгенівського випромінювання падає на поверхню кристалу під кутомковзання q (між падаючим променем і кристалографічною площиною) та збуджує атоми кристалічних грат сусідніх атомних площин, які стають джерелами вторинних когерентних хвиль і інтерферують між собою. Результат інтерференції хвиль визначається їх різницею ходу D =2d×sinq. Дифракційні максимуми спостерігаються у тих напрямках, в яких всі відбиті атомними площинами хвилі знаходять-
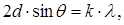
| ся у однаковій фазі. Ці напрямки визначаються формулою Вульфа-Брегга: |
де d – міжплощинна відстань, k – порядок спектру.
Відносно електромагнітних хвиль термін «дисперсія» розуміють, як спектральне розкладання складного випромінювання на його складові частини за частотами або довжинами хвиль. Причиною цього є залежність швидкості поширення хвилі від частоти або довжини хвилі V=f(n)=j(l). А оскільки V=c/n, то і показник заломлення середовища також виявляється залежним від частоти або довжини хвилі. І ця залежність також називається дисперсією. Наслідком дисперсії є розкладання пучка білого світла на монохроматичні складові при його проходженні через скляну призму, а кольорову смужку, яка при цьому утворюється, назвали суцільним спектром. Вперше це явище відкрите Ньютоном у 1672 році. Розглядаючи падіння світлового променя на бокову грань тригранної скляної призми із заломлюючим кутом q при її вер-
| y=q× (n-1). | шині, легко показати, що кут відхилення променя призмою становить: А оскільки n є функцією довжини хвилі, то промені різної довжини пі- |
сля проходження призми виявляться відхиленими на різні кути. Тому пучок білого світла і розкладається у спектр, причому із видимого максимально відхиляється світло фіолетового кольору, оскільки y~n~1/l. Кількісною мірою дисперсії є величина D=dn/dl, яка показує бистроту зміни показника заломлення n із довжиною хвилі l. Якщо D<0, тобто n зменшується при збільшенні l, така дисперсія називається нормальною. Якщо ж D>0 - n збільшується при зменшенні l - дисперсія називається аномальною. Вона спостерігається поблизу смуг поглинання речовини.
Явище зменшення енергії світлової хвилі при поширенні в речовині внаслідок її перетворення в інші види енергії, називається адсорбцією (поглинанням) світла. В результаті поглинання, інтенсивність світла при проходженні через речовину змен-
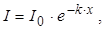
| шується, що описується законом Бугера-Ламберта: I0 та I – інтенсивності світлової хвилі на вході і на виході шару по- |
глинаючої речовини завтовшки х, k – коефіцієнт поглинання речовини, залежний від довжини хвилі падаючого світла, хімічної природи і стану поглинаючої речовини.
Явище поляризації полягає у виділенні світлових хвиль із певними напрямками коливань світлового вектора Е і спостерігається при відбиванні і заломленні світла на межі прозорих ізотропних діелектриків. Якщо природне світло падає на поверхню прозорого діелектрика під відмінним від нуля кутом, то відбитий і заломлений промені виявляються частково поляризованими. При цьому, у відбитому промені переважають коливання, перпендикулярні площині падіння, а у заломленому промені – коливання, що лежать у площині падіння. Ступінь поляризації залежить від кута падіння. Шотландський фізик Брюстер встановив, що при падінні природного світла на межу прозорих ізотропних діелектриків під кутом іВ, визначуваному спів-
| tg (iB) =n21, | відношенням: відбитий промінь буде повністю поляризованим, а заломлений – мак- |
симально поляризованим. У законі Брюстера n21=n2/n1 – відносний показник заломлення другого середовища відносно першого. При падінні природного світла під кутом Брюстера, відбитий і заломлений промені взаємно перпендикулярні.
Плоскополяризоване світло можна одержати, пропускаючи природне світло через поляризатори Р – пристосування, які пропускають коливання, паралельні головній площині поляризатора, і повністю або частково затримують коливання, перпендикулярні їй. Для виявлення і аналізу поляризованого світла, використовують такі ж поляризатори, які в цьому випадку називаються аналізаторами А. Французький фізик Малюс встановив, що інтенсивність світла, яке пройшло послідовно через поляризатор Р і аналізатор А, пропорційна квадрату косинуса кута a між їх головни-
| I=I0×cos2a, | ми площинами: де I0 – інтенсивність плоскополяризованого світла, падаючого на ана- |
лізатор (пропорційна квадрату амплітуди світлового вектора світла, яке пройшло че-рез поляризатор Е02), I - інтенсивність світла, яке вийшло із аналізатора (І~Е||2).
Деякі тверді і рідкі речовини мають здатність повертати площину поляризації світлової хвилі. Таку здатність називають оптичною активністю, а самі речовини – оптично активними (ОАР). Якщо між схрещеними поляризатором Р і аналізатором А розташувати ОАР, то темне поле зору в якійсь мірі прояснюється. Якщо А повернути на кут j, знову одержимо темне поле зору. Це означає, що після проходження ОАР світло залишається плоско поляризованим, але вона повертає площину поляризації світла на кут j. Кут повороту площини поляризації оптично активними кристалами і чистими рідинами визначається співвідношенням: j=a0×d, а водними активними розчинами j=a0×С×d, де d – товщина ОАР, a0 – питоме обертання – кут повороту площини поляризації шаром ОАР одиничної товщини і концентрації, С – масова концентрація ОАР у розчині.
ТЕСТОВІ ЗАВДАННЯ ІЗ РОЗДІЛУ “ХВИЛЬОВА ОПТИКА”
149. Який вид електромагнітного випромінювання має найбільшу довжину хвилі?
А) Ультрафіолетові промені. Б) Інфрачервоні промені. В) Гамма промені.
Г) Рентгенівські промені. Д) Видиме світло.
150. Який вид електромагнітного випромінювання має найбільшу частоту?
А) Гамма промені. Б) Рентгенівські промені. В) Ультрафіолетові промені.
Г) Інфрачервоні промені. Д) Видиме світло.
151. Світло випромінюється тілом, яке віддаляється від спостерігача. Як при цьому змінюється частота світла, який спостерігається?
А) Не змінюється. Б) Стає рівною нулю. В) Зміщується у бік фіолетової частини спектру.
В) Зміщується у область червоної частини спектру. Д) Відповідь неоднозначна.
152. Визначте частоту оранжевого випромінювання, якщо довжина його хвилі у вакуумі становить 600 нм.
А) 7,5×1014 Гц. Б) 1,25×1013 Гц. В) 2,5×1014 Гц. Г) 8,75×1015 Гц. Д) 5×1014 Гц.
153. Яка довжина хвилі у нанометрах відповідає частоті світла 6×1014 Гц?
А) 920 нм. Б) 380 нм. В) 760 нм. Г) 500 нм. Д) 240 нм.
154. Визначити частоту червоного випромінювання, довжина хвилі якого у вакуумі дорівнює 750 нм.
А) 4×1014 Гц. Б) 8×1014 Гц. В) 2×1014 Гц. Г) 6×1015 Гц. Д) 1×1014 Гц.
Date: 2015-08-06; view: 3272; Нарушение авторских прав