Вимоги до оформлення контрольних робіт

1. Семестрові контрольні роботи виконуються чорними або синіми чорнилами чи кульковою ручкою в звичайному шкільному зошиті, на обкладинці якого наводяться відомості студента про себе. Умови задач у контрольній роботі переписуються повністю, без скорочень. Для зауважень та приміток викладача на сторінках зошита потрібно залишаюти поля.

2. У кінці контрольної роботи вказується, яким підручником чи посібником студент користувався при вивченні фізики та розв'язку задач. Це робиться для того, щоб викладач у випадку необхідності міг вказати, що потрібно студенту вивчити (з цих матеріалів) для закінчення контрольної роботи. У контрольній роботі студент повинен розв'язати задачі того варіанту, номер якого збігається із його шифром. Контрольна робота виконана не за своїм варіантом не перевіряється.

3. Якщо контрольна робота при рецензуванні не зарахована, то студент повинен подати її на повторну рецензію, у яку потрібно включити ті задачі, розв'язки яких були невірними. Повторна робота подається разом із незарахованою. Зарахована контрольна робота подається викладачу на іспит або залік. Студент повинен вміти дати пояснення по суті розв'язку задач, які входять у контрольну роботу.

модуль № 5 “ОПТИКА”

Оптика – розділ фізики, в якому вивчаються закономірності випромінювання, поширення і взаємодії із речовиною світла. За традицією оптику прийнято підрозділяти на геометричну і фізичну. Геометрична оптика не розглядає природу світла. Її основними законами є прямолінійне поширення світла, його відбивання і заломлення на межах розділу прозорих середовищ. Фізична оптика вивчає проблеми, пов'язані із природою світла і світлових явищ. Згідно сучасним уявленням, світло має подвійну корпускулярно-хвильову природу (володіє курпускулярно-хвильовим дуалізмом): з одного боку, йому властиві хвильові властивості (явища інтерференції, дифракції, поляризації), а з іншого – світло є потоком частинок – фотонів, які мають нульову масу спокою і рухаються зі швидкістю, рівною швидкості світла у вакуумі. Корпускулярно-хвильовий дуалізм є проявом найзагальнішого взаємозв'язку двох основних форм існування матерії – речовини і поля.

Оскільки природа світла подвійна, для пояснення світлових явищ у оптиці використовуються дві теорії. З одного боку, світло є електромагнітною хвилею – описується хвильовою оптикою, а з іншого – це потік корпускул (частинок) – фотонів, і описується корпускулярною (квантовою) оптикою. Із часом погляди на природу світла змінювались, проте обмежитись однією із теорій для опису всіх властивостей світла не вдається.

ОСНОВИ ТЕОРІЇ ІЗ РОЗДІЛУ “ФОТОМЕТРІЯ”

Фотометрія – розділ оптики, що займається вимірюванням інтенсивності світла і його джерел. У фотометрії використовуються енергетичні величини, що характеризують енергетичні параметри оптичного випромінювання безвідносно до його дії на приймачі випромінювання, і світлові величини, що характеризують фізіологічні дії світла і оцінюються по дії на око (виходять із середньої чутливості ока) або інші приймачі випромінювання. Їх назви, позначення, визначення і одиниці вимірювання приведені у відповідних таблицях.

Енергетичні величини

Величина	Позна-чення	Визначення	Формула	Оди-ниця
Потік випроміню-вання	Fе	Кількість енергії dW, яку переносять світлові хвилі за одиницю часу dt.		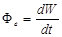Вт
Енергетична світ-ність (випроміню-ваність)	Re	Потік випромінювання dFe, що випромінюється по верхнею, на одиницю площини перерізу dS, через який він проходить.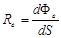
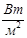
Енергетична сила світла (сила випро мінювання)	Ie	Потік випромінювання від джерела світла dFe, на одиницю тілесного кута dw, в межах якого він по-ширюється.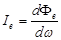
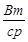
Енергетична яск-равість (промени-стість)	Be	Сила світла dIe елементу поверхні, що випромінює на одиницю площі dS його проекції на площину, перпендикулярну напрямку спостереження.

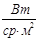
Світлові величини

Величина	Позна-чення	Визначення	Формула	Оди-ниця
Світловий потік	F	Потужність оптичного випромінювання по світловому відчуттю, яке ним спричиняється.		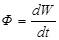лм люмен
Світність	R	Світловий потік dF на одиницю площини dS, через яку він проходить.
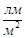
Освітленість	Е	Світловий потік від джерела світла dF, що припадає на одиницю площі dS освітлюваної поверхні.		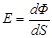лк (люкс)

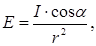R=r×E,   R=p×B.

Точкове джерело силою світла I створює на площадці, віддаленій від нього на відстані r освітленість: де a - кут падіння проміння. Якщо світність тіла R обумовлена його освітленістю E, то: де r - коефіцієнт розсіяння (відбивання). Якщо тіло випромінює за законом Ламберта (яскравість не залежить від напрямку), то світність R і яскравість В зв'язані співвідношенням:

ТЕСТОВІ ЗАВДАННЯ ІЗ РОЗДІЛУ “Фотометрія”

1. Світло від електричної лампи силою І=200 кд падає під кутом a=45⁰ на робоче місце, освітленість якого Е=141 лк. На якій відстані r від робочого місця знаходиться лампа?

А) 1,75 м. Б) 1,0 м. В) 1,25 м. Г) 2,0 м Д) 0,75 м.

2. За умов попередньої задачі визначте висоту h, на якій висить освітлювальна лампа над робочим місцем.

А) 0,86 м. Б) 0,48 м. В) 1,12 м. Г) 0,71 м. Д) 0,64 м.

3. Під час весняного та осіннього рівнодення Сонце стоїть на екваторі у зеніті. У скільки разів у цей час освітленість поверхні Землі на екваторі більша за освітленість поверхні Землі у Санкт-Петербурзі, широта якого j=60⁰? (Сонячні промені вважати паралельними).

А) У 1,33 рази. Б) У 0,86 разів. В) У 1,41 рази. Г) У 2 рази. Д) У 1,73 рази.

4. Над центром круглого столу діаметром d=2 м на висоті h=0,9 м висить лампа, сила світла якої дорівнює I=100 кд. Вважаючи лампу точковим джерелом світла, визначте освітленість Е на краю столу.

А) 37 лк. Б) 118 лк. В) 74 лк. Г) 21 лк. Д) 56 лк.

5. У центрі круглого столу діаметром d=1,2 м знаходиться настільна лампа силою I=150 кд на висоті h=40 см від поверхні столу. Визначте освітленість E на краю столу.

А) 40 лк. Б) 120 лк. В) 200 лк. Г) 80 лк. Д) 160 лк.

6. У центрі круглого столу діаметром d=1,6 м висить люстра із чотирьох електричних ламп силою I=80 кд кожна на висоті h=2 м від поверхні столу. Визначте ос-вітленість Е на краю столу.

А) 8 лк. Б) 64 лк. В) 16 лк. Г) 32 лк. Д) 48 лк.

7. При фотографуванні предмет освітлюється електричною лампою, розташованою на відстані r₁=2 м від нього. У скільки разів потрібно збільшити експозицію Dt, якщо цю лампу відсунути на відстань r₂=3 м від предмета?

А) У 1,5 рази. Б) У 2,25 разів. В) У 2 рази. Г) У 1,75 разів. Д) У 2,5 разів.

8. Визначити освітленість поверхні Землі Е, яку здійснюють нормальні до неї сонячні промені, якщо яскравість Сонця В=1,2×10⁹ кд/м², а коефіцієнт відбивання від земної поверхні r=0,3. Радіус Сонця r_c становить 6,95×10⁸ м, а середній радіус земної орбіти R₃ дорівнює 1,5×10¹¹ м.

А) 4,3×10³ лк. Б) 2,4×10⁵ лк. В) 8,6×10⁴ лк. Г) 9,8×10³ лк. Д) 1,2×10⁴ лк.

9. Спіраль електричної лампи із силою світла І=100 кд вміщена у матову сферичну колбу діаметром d=5 см. Визначте світність лампи R, якщо утратами світла у оболонці лампи можна знехтувати.

А) 1,6×10⁵ лк/м². Б) 6,8×10⁴ лк/м². В) 9,4×10⁵ лк/м². Г) 3,2×10³ лк/м². Д) 4,8×10⁴ лк/м².

10. Визначте яскравість електричної лампи В за умов попередньої задачі.

А) 3,8×10³ кд/м². Б) 1,4×10⁴ кд/м². В) 7,2×10⁵ кд/м². Г) 5,1×10⁴ кд/м². Д) 8,6×10⁵ кд/м².

11. У виготовленій із прозорого скла електричній лампі світнім тілом є розжарена кулька діаметром d=3 мм, і сила її світла І становить 85 кд. Визначте яскравість В цієї лампи.

А) 5,7×10⁵ кд/м². Б) 3,4×10⁶ кд/м². В) 9,3×10⁷ кд/м². Г) 7,6×10⁶ кд/м². Д) 1,2×10⁷ кд/м².

12. За умов попередньої задачі визначте освітленість поверхні, що лежить на відстані r=5 м при нормальному падінні світла.

А) 5,2 лк. Б) 3,4 лк. В) 13,6 лк. Г) 6,8 лк. Д) 1,7 лк.

13. Сферична електрична лампа виготовлена із матового скла Діаметр її колби становить 6 см, а сила світла I дорівнює 85 кд. Визначте яскравість В цієї лампи.

А) 7×10³ кд/м². Б) 5×10⁵ кд/м². В) 3×10⁴ кд/м². Г) 2×10³ кд/м². Д) 9×10⁴ кд/м².

14. На лист білого паперу розміром 20´30 см нормально до його поверхні падає світловий потік F=120 лм. Визначте освітленість Е цього паперового листа.

А) 8×10³ лк. Б) 4×10⁴ лк. В) 3×10⁵ лк. Г) 2×10³ лк. Д) 9×10⁴ лк.

15. Визначте світність R паперового листа за умов попередньої задачі, якщо коефіцієнт його розсіювання r=0,75.

А) 9,2×10⁴ лм/м². Б) 1,5×10³ лм/м². В) 3,4×10⁴ лм/м². Г) 8,7×10³ лм/м². Д) 2,3×10⁵ лм/м².

16. Визначте яскравість В паперового листа за умов попередньої задачі.

А) 478 кд/м². Б) 119 кд/м². В) 356 кд/м². Г) 524 кд/м². Д) 237 кд/м².

17. Якою мусить бути освітленість Е листа паперу, щоб його яскравість В дорівнювала 10⁴ кд/м², якщо коефіцієнт його розсіювання r становить 0,75.

А) 2,3×10⁵ лк. Б) 6,8×10³ лк. В) 1,1×10⁴ лк. Г) 8,4×10⁵ лк. Д) 4,2×10⁴ лк.

18. Лист паперу розміром 10´30 см освітлюється світлом від лампи силою I=100 кд, причому на нього падає 0,5% від усього світлового потоку F₀, який посилає ця лампа. Визначте освітленість Е цього листа паперу.

А) 108 лк. Б) 165 лк. В) 210 лк. Г) 54 лк. Д) 246 лк.

19. Електрична лампа посилає у всі боки щохвилини 122 Дж світлової енергії. Визначте коефіцієнт корисної дії h світлової віддачі, якщо лампа споживає потужність P=100 Вт.

А) 4,5%. Б) 1,0%. В) 7,5%. Г) 2,0%. Д) 1,5%.

20. Електрична лампа силою І=100 кд щохвилини випромінює 120 Дж світлової енергії. Визначити механічний еквівалент світла k для даного світлового джерела (k=Р₀/F₀ [Вт/лм]).

А) 1,6×10^-3 Вт/лм. Б) 2,4×10^-2 Вт/лм. В) 9,1×10^-3 Вт/лм. Г) 7,2×10^-4 Вт/лм. Д) 5,6×10^-2 Вт/лм.

ОСНОВИ ТЕОРІЇ ІЗ РОЗДІЛУ “Геометрична оптика”

 

Це розділ оптики, в якому закони поширення світла розглядається на основі уявлення про світлові промені – нормальні до хвильових поверхонь лінії, уздовж яких поширюється потік світлової енергії.

Закон прямолінійного поширення світла: світло у оптично однорідному середовищі поширюється прямолінійно.

Закон незалежності світлових пучків: дія, спричинена окремим світловим пучком, не залежить від того, чи діють одночасно з ним інші світлові пучки або вони повністю усунені.

Закон відбивання світла: відбитий від межі розподілу двох прозорих середовищ промінь лежить у одній площині із падаючим променем та перпендикуляром, проведеним до межі розподілу із точки падіння. Кут відбивання a¢ (між відбитим променем і перпендикуляром до межі) дорівнює куту падіння a (між падаючим променем і перпендикуляром): a¢=a.

Закон заломлення світла: промінь падаючий, промінь заломлений і перпендикуляр, проведений до межі розподілу із точки падіння, лежать у одній площині; відношення синуса кута падіння до синуса кута заломлення для певних двох середо-

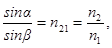
вищ є постійною величиною: де n21 – відносний показник заломлення другого середовища відносно першого, n2 і n1 – абсолютні показники заломлення кожно-

го середовища. n=c/V, де с – швидкість поширення світла у вакуумі, V – швидкість світла у даному середовищі.

Якщо світло поширюється із оптично більш густого середовища (середовища із більшим показником заломлення) у оптично менш густе середовище (середовище із меншим показником заломлення (тобто, n₁>n₂)), згідно закону заломлення світла:

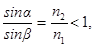
тобто a<b. При збільшенні кута падіння a збільшується і кут заломлення b доти, доки при деякому куті падіння aгр, який називають граничним кутом, кут заломлення не виявиться рівним p /2. При куті па-

діння a=a_гр, інтенсивність заломленого променя обертається в нуль, а інтенсивність відбитого стає рівною інтенсивності падаючого. Це явище називається повним внутрішнім відбиванням. При кутах падіння a>a_гр падаючий промінь не заломлюється, а повністю відбивається у перше середовище від межі розподілу із оптично менш

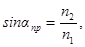
густим середовищем. Для граничного кута повного внутрішнього від-бивання aгр, закон заломлення світла набуває вигляду: оскільки у цей момент sin(b)=sin(p/2) =1. Це явище використовується

у призмах повного відбивання, які дозволяють повертати світлові пучки на 90⁰, розвертати зображення на 180⁰ або перевертати його.

Якщо монохроматичний пучок світла падає на бокову грань прозорої призми, показник заломлення матеріалу якої n, а кут при її вершині J (заломлюючий кут), то після двократного заломлення на лівій і правій гранях призми падаючий пучок відхилиться від свого первинного напрямку до основи призми на кут j. Використовуючи геометричні побудови променя при проходженні призми неважко переконатись, що кут відхилення променя призмою може бути визначений за формулою:

j=a1+a2-J.	де a1 – кут падіння променя на одну грань призми, a2 – кут заломлення променя на іншій її грані. Вважаючи кути J та a1 малими, і за-
j=J×(n-1).	писавши закон заломлення світла для обох граней призми, цьому співвідношенню легко надати вигляду:

Лінзаминазиваються прозорі тіла, обмежені двома поверхнями (одна з них звичайно сферична, іноді циліндрична, а друга – сферична або плоска), які заломлюють світлові промені і здатні формувати оптичні зображення предметів. Тонкоюназивається лінза, у якій її товщина d (відстань між обмежуючими її поверхнями) значно менша за радіуси кривини цих поверхонь R (d<<R). Радіус кривини опуклої поверхні лінзи вважається позитивним, а вгнутої – негативним.

 

Форма лінзи
Назва	Дво- опуклі	Плоско- опуклі	Дво- вгнуті	Плоско- вгнуті	Опукло- вгнуті	Вгнуто- опуклі
Радіуси	R1>0, R2<0	R1>0, R2=¥	R1<0, R2>0	R1<0, R2=¥	R1>R2>0	R1>R2<0
Фокусна відстань	F>0	F>0	F>0	F<0	F<0	F<0

 

Основні елементи лінзи: 1) Головна оптична вісь – пряма, що проходить че-рез центри кривини поверхонь лінзи. 2) Оптичний центр лінзи – точка О, яка ле-жить на головній оптичній осі і має властивість, що промені проходять через неї не заломлюючись. 3) Фокус лінзи – точка F, яка лежить на головній оптичній осі, у якій перетинаються промені параксиального (приосьового) світлового пучка, що поширюється паралельно головній оптичній осі (у кожної лінзи два фокуси). 4) Фокусна відстань F – відстань між оптичним центром лінзи і її фокусом. 5) Побічна оптична вісь – будь-яка пряма, що проходить через оптичний центр лінзи і не співпадає із головною оптичною віссю.

Якщо у середині лінза товща, ніж на краях, вона називається збірною, оскільки пучок паралельного головній оптичній осі світлового проміння збирає у фокусі, що лежить по іншу сторону від джерела світла. Якщо у середині лінза тонша, ніж на краях, вона називається розсіюючою, оскільки розсіює падаючий на неї пучок паралельного головній оптичній осі світлового проміння.

Побудова зображення предметів у лінзах здійснюється за допомогою таких променів: 1) Променя, що проходить через оптичний центр лінзи і не змінює свого напрямку; 2) Променя, що іде паралельно головній оптичній осі; після заломлення в лінзі цей промінь (або його продовження) проходить через другий фокус лінзи; 3) Променя (або його продовження), що проходить через перший фокус лінзи; після заломлення в ній він виходить із лінзи паралельно її головній оптичній осі.

 

⇐ Предыдущая25262728293031323334Следующая ⇒

Date: 2015-08-06; view: 442; Нарушение авторских прав

Понравилась страница? Лайкни для друзей: