Степенные ряды. Теорема Абеля. Ряды Тейлора и Маклорена

1. Пусть задана последовательность чисел:

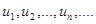
Выражение

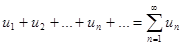
называется числовым рядом; числа 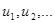называются членами ряда; число 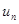называется общим членом ряда.

Сумма п первых членов ряда

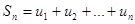
называется п-ой частичной суммой ряда.

Если существует конечный предел

,

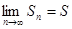то число S называют суммой ряда 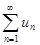, а сам ряд называют сходящимся. Если же предел 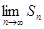не существует или равен бесконечности, то говорят, что ряд расходящийся.

Рассмотрим ряд

.

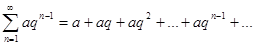Это сумма геометрической прогрессии, q – знаменатель прогрессии. Если 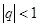, прогрессия называется убывающей. Сумму 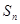первых п членов этой прогрессии находят по формуле

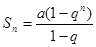. (8.1)

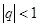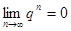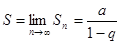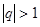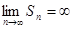Если , то и . Значит, бесконечно убывающая геометрическая прогрессия всегда сходится. Если , то и прогрессия расходится.

Если числовой ряд сходится, то разность 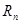между его суммой S и частичной суммой 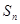называется п-м остатком ряда, то есть

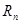= S - .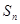

Остаток ряда 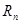является той погрешностью, которая получится, если вместо S взять 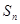. Поскольку 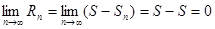, то, взяв достаточно много первых членов сходящегося ряда, можно сумму этого ряда вычислить с любой точностью.

Отсюда становится понятным, что основной задачей теории рядов является исследование сходимости ряда. Задача нахождения суммы сходящегося ряда имеет второстепенное значений, поскольку после установления сходимости ряда его сумма может быть легко найдена.

Свойства рядов

1. Если ряды 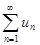и 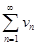сходятся и их суммы U и V, то ряд 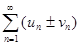также сходится и его сумма равна U 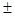V.

2. Если ряд 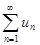сходится и его сумма равна S, то ряд 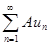, где А=const, также сходится и его сумма равна АS.

3. Конечное количество членов ряда на его сходимость не влияет.

Теорема 8.1. (необходимое условие сходимости ряда). Если ряд 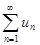сходящийся, то предел его общего члена равен нулю

.

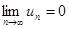Доказательство.

_.

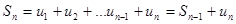Отсюда 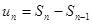. Если ряд сходящийся, то 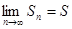и 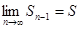. Поэтому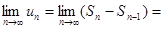 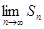- - 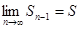S =0.

Следствие. Если 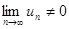, то ряд 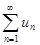расходящийся.

Замечание. Условие 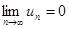является необходимым условием сходимости ряда, но не достаточным, то есть выполнение этого условия не гарантирует сходимости ряда.

Пример 8.1. Рассмотрим ряд .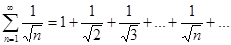

Хотя необходимое условие сходимости ряда выполняется,

,

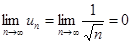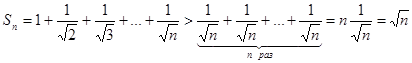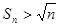
но , 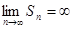и ряд является расходящимся, несмотря на то, предел его общего члена равен нулю.

2. Первый признак сравнения. Пусть члены рядов 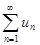и 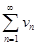удовлетворяют условию

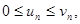п =1,2,3,….

Тогда, если ряд 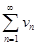сходящийся, то сходящийся и ряд 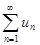, а если ряд 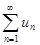расходящийся, то расходящийся и ряд .

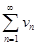Второй признак сравнения. Пусть члены рядов 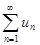и 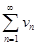положительны, причём существует конечный предел

.

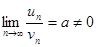Тогда оба ряда сходятся или расходятся одновременно.

Сравнивать ряди удобно с рядам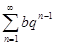и и 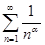, сходимость которых известна.

Ряд 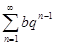является суммой бесконечной геометрической прогрессии. Он сходится при 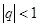(когда прогрессия убывающая) и расходится при .

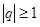Ряд 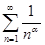называется обобщенным гармоническим рядом. Он сходится при 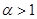и расходится при .

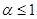Признак Даламбера. Если для членов ряда 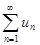с положительными членами 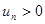существует предел

,

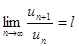то ряд будет сходящимся при 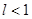и расходящимся при .

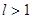Радиальный признак Коши. Если для членов ряда 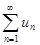с положительными членами 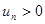существует предел

,

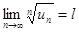то ряд будет сходящимся при 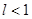и расходящимся при .

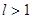Интегральный признак Коши. Если 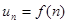, где 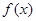- положительная невозрастающая непрерывная функция, то ряд 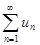и интеграл 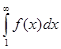сходятся или расходятся одновременно.

Применим интегральный признак Коши для исследования обобщенного гармонического ряда .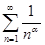

1. 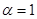, 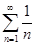- гармонический ряд.

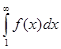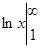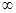= , = = - расходится.

2. , = ,

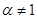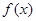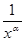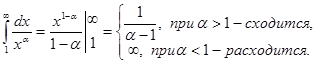
Значит, ряд 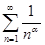сходится при 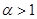и расходится при .

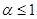Знакочередующимися называют ряды, в которых знаки членов строго чередуются

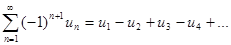, где 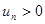. (8.2)

Признак Лейбница. Если для членов ряда (8.2) выполняется два условия:

1) _.

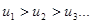2) ,

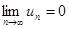то этот ряд сходится, его сумма положительна и не превышает .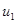

Следствие. Если сумму S сходящегося ряда (8.2) заменить суммой S 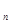его п первых членов, то допущенная при этом погрешность не превышает абсолютной величины первого из отброшенных членов, то есть

.

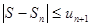Это следствие широко используется при приближённых вычислениях.

Знакопеременными называются ряды, у которых члены имеют разные знаки.

Знакопеременный ряд 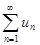называется абсолютно сходящимся, если сходится ряд 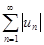, составленный из абсолютных величин его членов.

Знакопеременный ряд называется условно сходящимся, если он сходящийся, а ряд, составленный из абсолютных величин его членов, расходящийся.

Теорема 8.2. Любой абсолютно сходящийся ряд сходится.

Для чего надо различать абсолютную и условную сходимость? Как ответ на этот сформулируем две теоремы.

Теорема 8.3. Абсолютно сходящийся ряд остаётся абсолютно сходящимся при произвольной перестановке его членов. При этом сумма ряда не зависит от порядка его членов.

Теорема 8.4. Члены условно сходящегося ряда всегда можно переставить так, чтобы его сумма равнялась наперёд заданному числу. Более того, можно так переставить члены условно сходящегося ряда, что новый ряд будет расходящимся.

Интересные свойства условно сходящихся рядов показывает такой пример.

Пример 8.2. Пусть 1- .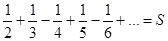

Запишем ряд иначе:

=

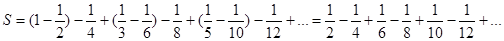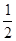= (1- ,

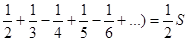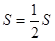
2=1?

Значит, переставляя члены условно сходящегося ряда, получили неверный результат.

3. Ряд 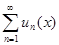, членами которого является функцией от х, называется функциональным рядом. Давая переменной х конкретные числовые значения, получим разные числовые ряды, которые могут быть сходящимися или расходящимися.

Множество всех значений х, для которых ряд 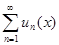сходящийся, называется областью сходимости этого ряда.

Функциональный ряд вида 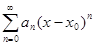(8.3)

где 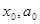- числа, называется степенным рядом.

Переобозначив 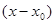на х, ряд (8.3)всегда можно свести к виду 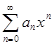(8.4)

Для простоты будем изучать ряды вида (8.4). Ряд (8.4) всегда сходится, по крайней мере, в точке х =0.

Теорема Абеля. (1802-1829). Если ряд (8.4) сходящийся при 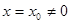, то он абсолютно сходящийся для всех значений х, что удовлетворяют неравенству 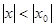, то есть в интервале 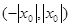. Если при 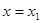ряд (8.4) расходящийся, то он расходящийся для всех значений х, что удовлетворяют неравенству .

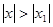Из теоремы Абеля следует, что если ряд (8.4) сходится хотя бы в одной точке 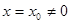, то существует такое число R >0, что при 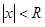ряд сходится абсолютно, а при 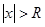расходится. Это число R называют радиусом сходимости степенного ряда, а интервал 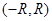- его интервалом сходимости.

Радиус сходимости ряда (8.5) можно найти по формулам

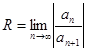или 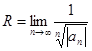. (8.5)

Вывод. Чтобы найти область сходимости ряда (8.5) надо:

1) найти интервал сходимости 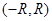ряда, применяя к ряду 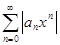признаки Даламбера и Коши, или пользуясь формулами (8.5);

2) исследовать сходимость ряда на концах интервала сходимости, то есть в точках .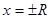

В середине интервала сходимости степенные ряды можно почленно интегрировать и дифференцировать, причём полученные при этом ряды будут иметь тот же радиус сходимости, что и исходный ряд.

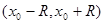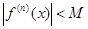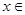
Если функция f (х) в интервале имеет производные всех порядков и существует такое число М >0, что , , 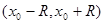п =0, 1, 2,…, где 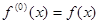, то функцию f (х) можно разложить в ряд Тейлора

.

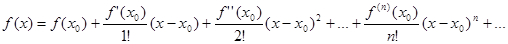При 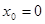ряд Тейлора имеет вид

и называется рядом Маклорена.

Приведём примеры рядов Маклорена некоторых элементарных функций.

;

;

;

;

= ;

;

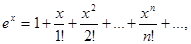
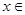
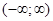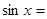
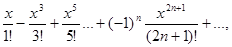
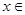
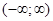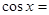
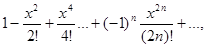
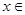
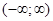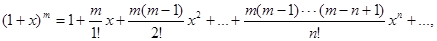
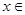
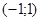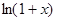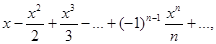
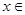
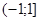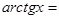
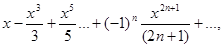
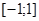Ряды широко используются для приближённого вычисления функций, интегралов, для приближённого интегрирования дифференциальных уравнений.

Date: 2015-07-27; view: 467; Нарушение авторских прав