Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами

1. Линейным дифференциальным уравнением первого порядка называется уравнение вида

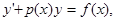(7.4)

где 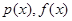- известные функции переменной х.

Термин «линейное уравнение» поясняется тем, что неизвестная функция у и её производная у ’ входят в уравнение в первой степени, то есть линейно.

Линейное дифференциальное уравнение первого порядка всегда интегрируемо в квадратурах, поскольку его можно всегда свести к двум уравнениям с разделяющимися переменными таким образом (методом Бернулли).

Будем искать решение уравнения (7.4) в виде произведения

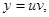(7.5)

где 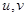- неизвестные функции х. Находя производную

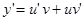
и подставляя значение у и у’ в уравнение (7.5), получим

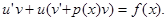(7.6)

Выберем функцию так, чтобы выражение в скобках равнялось нулю. Для этого надо решить уравнение с разделяющимися переменными.

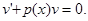
Решая его, находим

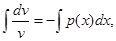
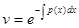. (7.7)

Постоянную интегрирования в выражении (7.7) не пишем, поскольку нам достаточно найти только какую-нибудь одну функцию , которая преобразовывает в ноль выражение в скобках в уравнении (7.6).

Подставляя (7.7) в (7.6), получим

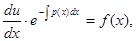
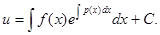(7.8)

Подставляя (7.7) и (7.8) в (7.5), найдём общее решение уравнения (7.4):

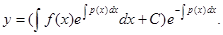(7.9)

Замечание. На практике помнить формулу (7.9) не обязательно: достаточно лишь помнить, что линейные дифференциальные уравнения первого порядка, а также уравнения Бернулли, решаются методом Бернулли с помощью подстановки .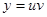

Уравнением Бернулли называется уравнение вида

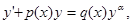
где 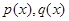- известные функции х, .

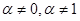2. Комплексным числом называется выражение

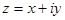, (7.10)

где х, у – действительные числа, а символ i – мнимая единица, которая определяется условием 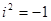. При этом число х называется действительной частью комплексного числа z и обозначается 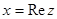, а у – мнимой частью z и обозначается 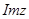(от французских слов: reel – действительный, imaginare – мнимый). Выражение (7.10) называется алгебраической формой комплексного числа.

Два комплексных числа 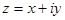и 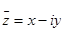, которые отличаются только знаком мнимой части, называются сопряжёнными.

Два комплексных числа 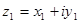и 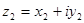считаются равными тогда и только тогда, когда равны их действительные и мнимые части:

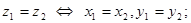
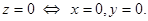
Комплексные числа можно изображать на плоскости. Так число (7.10) изображается в прямоугольной системе координат точкой М (х; у). Такая плоскость называется комплексной плоскостью переменной z, ось Ох называется действительной, у

а ось Оу – мнимой.

При у =0 комплексное число 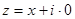является одновременно

у М (х; у)

действительным числом. Поэтому действительные числа являются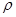

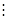
отдельным случаем комплексных, они изображаются на оси Ох.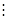

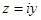Комплексные числа , в которых х =0, называются чисто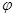

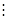
мнимыми; такие числа изображаются на оси Оу.

0 х х

Полярные координаты точки М (х; у) на комплексной плоскости называются модулем и аргументом комплексного числа и обозначаются

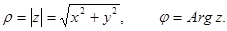
Поскольку 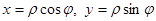, то по формуле (7.10) имеем

.

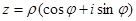Это выражение называется тригонометрической формой комплексного числа z.

Модуль комплексного числа определяется однозначно, а аргумент – с точностью до 2 :

.

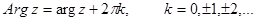Здесь 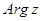- общее значение аргумента, а 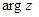- главное значение аргумента, которое находится на промежутке [0; 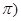и отсчитывается от оси Ох против часовой стрелки.

Если 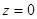, то считают, что 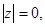а 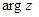- неопределён.

Арифметические действия над комплексными числами, заданными в алгебраической форме, выполняются по обычным правилам действий над двучленами с учётом того, что 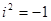. Так, если

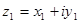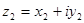, , то

1)

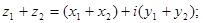
2)

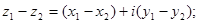
3)

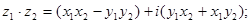
4) .

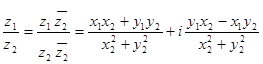Рассмотрим действия над комплексными числами в тригонометрической форме.

Пусть

, .

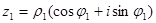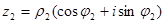Тогда

=

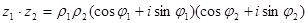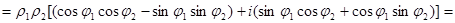
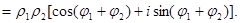
Значит, при умножении комплексных чисел их модули перемножаются, а аргументы складываются. Это правило распространяется на произвольное конечное число множителей. В частности,

.

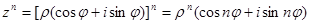Последняя формула называется формулой Муавра.

При делении комплексных чисел имеем

.

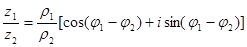Рассмотрим извлечение корня из комплексного числа. Если для данного комплексного числа 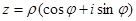надо найти корень п- й степени 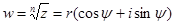, то по определению корня и формуле Муавра имеем

.

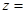
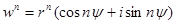
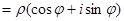Отсюда

, .

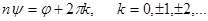Поскольку r и 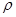положительные, то 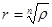, где под корнем понимают его арифметическое значение. Поэтому

.

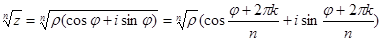Давая k значения 0,1,2,…, п -1, получим п разных значений корня. Для других значений k аргументы будут отличаться от найденных на число, кратное 2 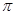, поэтому значения корня будут совпадать с уже найденными.

Известно, что показательную функцию с мнимым показателем можно выразить через тригонометрические функции по формуле Эйлера 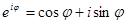. Отсюда следует, что всякое комплексное число можно записать в форме 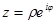, которая называется показательной формой комплексного числа z.

3. Уравнение вида

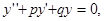(7.11)

где р, q – постоянные числа, называется линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами. Для его решения сначала надо составить характеристическое уравнение

(7.12)

В зависимости от корней 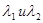уравнения (7.12) общее решение уравнения (7.11) приобретает один из таких видов:

1) 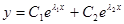, если 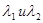действительные и ;

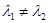2) 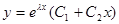, если 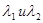действительные и ;

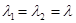3) 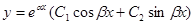, если , ().

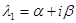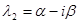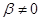Пример 7.8. Решить уравнение

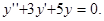(7.13)

Решение. Сначала составим и решим соответствующее характеристическое уравнение:

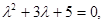D = 3²- 4*5= -11,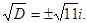

Характеристическое уравнение имеет два сопряжённых корня:

.

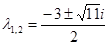Поэтому общее решение уравнения (7.13) будет таким:

.

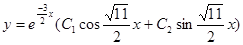Лекция 17. Тема – Ряды. Числовые ряды. Признаки сходимости. Степенные ряды.

План.

Основные понятия. Необходимое условие сходимости ряда.

Date: 2015-07-27; view: 433; Нарушение авторских прав