Выбор тестовой задачи

При анализе устойчивости многошаговых методов обращаются к простейшей задаче Коши

,

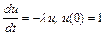где 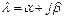– в общем случае комплексная величина. Такой выбор тестовой задачи объясняется тем, что устойчивая линейная система (ее решение стремится к нулю) общего вида

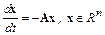
с действительной 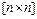-матрицей 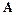простой структуры преобразованием

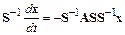
приводится к виду

,

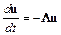где 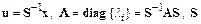– неособенная матрица преобразования, 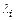– собственные значения матрицы 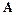(в общем случае комплексные величины). Таким образом, каждое уравнение

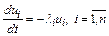
преобразованной устойчивой линейной системы является простейшим дифференциальным уравнением, совпадающим по форме с тестовым уравнением привлекаемой задачи Коши.

Точное решение тестовой задачи имеет вид

.

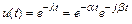Если 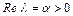, то 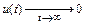при любом значении 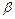. Применяя численный метод с постоянным шагом 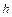к тестовому уравнению, получим последовательность 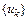. Если 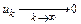, то такой метод является устойчивым.

Date: 2015-07-27; view: 384; Нарушение авторских прав