Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Явление жесткости
Ограниченная устойчивость численного метода является серьезным недостатком при решении так называемых жестких систем.
Рассмотрим дифференциальное уравнение первого порядка
,
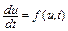для которого уравнение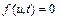 
имеет единственное решение
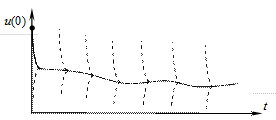
Рис. 10.3. К определению жесткости дифференциального уравнения
|
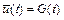. Любая интегральная кривая такого дифференциального уравнения характеризуется двумя участками с существенно различным поведением решения (см. рис. 10.3), причем первый участок значительно меньше второго. Первый участок с быстрым изменением функции 
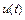отражает стремление интегральной кривой к графику функции 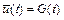и называется пограничным слоем. На втором участке интегральная кривая практически совпадает с графиком 
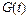. Однако даже при небольшом отклонении от графика 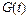в любой его точке производная 
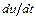резко возрастает по сравнению с производной 
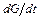. Именно по этой причине малый шаг интегрирования, используемый при воспроизведении быстропротекающего участка, не может быть существенно увеличен вне пограничного слоя в явных методах численного интегрирования.
Рассмотрим примеры жестких систем.
1. Простейшее дифференциальное уравнение
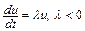(10.1)
может быть жестким (рис. 10.4), если интервал наблюдения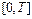 
зна-
Рис. 10.4. Семейство решений уравнения (10.1)
чительно превосходит величину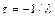 
. Решением такого уравнения является функция 
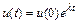. Пунктирные линии на рис. 10.4 соответствуют различным значениям 
.
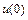2. Для иллюстрации явления жесткости дифференциальных уравнений может быть полезной также любая система линейных ОДУ, матрица которой характеризуется большим разбросом собственных значений, например система
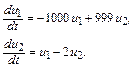(10.2)
Здесь собственные числа матрицы есть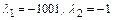 
.
Решение этой системы (рис. 10.5)
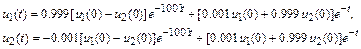
содержит быструю составляющую как для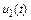 
, так и для 
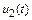, хотя по амплитуде быстрая составляющая функции 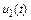значительно превосходит аналогичную компоненту функции 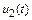(ее на рис. 10.5 в таком масштабе отобразить не удалось).
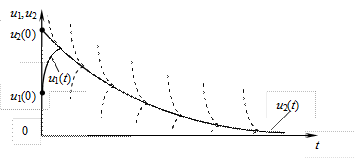
Рис. 10.5. Решение жесткой системы ОДУ (10.2)
Завершая краткую характеристику свойства жесткости дифференциальных уравнений, отметим, что при решении научных задач жесткость уравнений является скорее правилом, чем исключением. По этой причине для таких задач разработаны специальные методы численного интегрирования.
Лекция 11
Date: 2015-07-27; view: 372; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |