Выводы к главе. 1. Тангенциальную скорость Vr вращательного движения тел и кинетическую энергию их вращения следует считать мнимыми величинами

1. Тангенциальную скорость Vr вращательного движения тел и кинетическую энергию их
вращения следует считать мнимыми величинами.
2. При вращении тела скорость его движения во времени принимает значения, большие единицы. Эксперименты с ускорением мезонов в циклических ускорителях могут выявить это.
3. В отличие от импульса поступательного движения тела, в выражении для мнимого импульса вращательного движения Рг входит произведение скоростей движения тела в пространстве ß r и во времени у r а не их отношение.
4. График зависимости Pr отVr имеет экстремум-минимум при 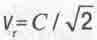, а график зависимости кинетической энергии вращения тела от ут имеет минимум при .
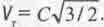5. Основное уравнение теории движения можно получить возведением в квадрат дифференциала комплексного числа , правильно описывающего точку в нашем пространстве - времени.
6. Полный импульс тела получается векторным сложением ортогональных импульса движения) тела в пространстве P = mV и "импульса покоя" этого тела Р0= m0С. "Импульс покоя" тела Р0 получается векторным сложением ортогональных импульса движения тела во времени 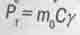и классического импульса Pv= m0V.
7. Связь между полной энергией тела 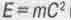и импульсом тела P выражается известным уравнением 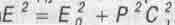котором Е0 - энергия покоя данного тела, а вот величина P = mV при поступательном движении тела в пространстве P = im0Vr - при вращательном движении тела, в чем состоит отличие от известного в СТО уравнения.
8.Из выражения для квадрата комплексной скорости в теории движения 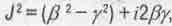мнимую часть которого СТО упустила, следует, что всякое поступательное движение тела в пространстве должно сопровождаться вращением тела или кручением пространства, которое характеризует отклонение линии от плоской формы. Они описываются мнимой частью этого выражения. Вращение и кручение являются неотъемлемыми свойствами не только движения в пространстве, но и самого пространства-времени.
9. Всякое вращающееся тело порождает торсионные поля - поля кручения. Эти выводы хорошо согласуются с представлениями о торсионных полях, развитыми в работах Г. И. Шилова и А. Е. Акимова.
10. Переносчиками торсионных взаимодействий (квантами торсионного поля) являются, по-видимому, нейтрино, которые, согласно теории движения, являются тахионами и движутся со сверхсветовыми скоростями.
11. Представление о том, что вращательное движение мнимое, существенно изменяет выражение для плоских волн де Бройля, описывающих вероятность нахождения частицы в точках пространства при ее вращении или обращении по орбите. Теперь пси-функция оказывается стоячей волной, а вблизи от оси вращения вероятность нахождения частицы уже не нулевая, что обеспечивает необходимую плавность изменения - функции и разрешает ряд трудностей теорий де Бройля и Г. Шилова.
12. Пси-поле (торсионное поле), описываемое так модернизированными плоскими волнами де Бройля, имеет острую направленность вдоль оси вращения тела, генерирующего это поле, и возникает во всех точках пространства мгновенно, что означает бесконечно большую скорость распространения пси-волн торсионного поля.

Date: 2015-07-27; view: 645; Нарушение авторских прав