Волны де Бройля и торсионные поля

Мы уже упоминали в разделе 4.3, что Луи де Бройль в 1924 г. ввел понятие "волн материи", групповая скорость которых Vгр совпадает со скоростью движения частицы в пространстве, а фазовая 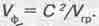. Для движущихся частиц, масса покоя которых не равна нулю, Vф может быть только больше скорости света. Но насколько материальны "волны материи"? И что за волновой процесс они описывают?
Э. Шредингер высказал в свое время предположение о том, что волновой пакет этих волн, локализованный в малой области пространства, представляет элементарную частицу. Но наличие дисперсии, то есть зависимости фазовой скорости волн де Бройля от их частоты даже в вакууме, должно было приводить к тому, что волновые пакеты, состоящие из таких волн, расплываются со временем. А элементарные частицы стабильны.
Большинство теоретиков до сих пор полагают, что фазовая скорость волн де Бройля имеет чисто символическое значение и не отражает никаких конкретных процессов. Но некоторые физики называют волну де Бройля "волной-пилотом", которая опережает движение частицы и как бы разведывает ей путь. В результате частица "знает" через какое из двух отверстий перегородки, установленной на ее пути, ей проскочить, а после проскоков через эти отверстия многих следующих друг за другом частиц на экране за перегородкой получают интерференционную картину, обусловленную интерференцией "волн-пилотов", проходивших одновременно через оба отверстия, хотя каждая из частиц пролетала только через одно из них, а каждая последующая частица начинала движение только после того, как предыдущая уже закончила свой путь [71]. Получается, что не такой уж нереальной оказывается сверхсветовая фазовая скорость волн де Бройля. Ведь частицы в этих экспериментах летели почти со световой скоростью, а волна де Бройля намного опережала их. Плоская бегущая волна де Боойля намного опережала их.
Плоская бегущая волна де Бройля

(5.26)

описывает, как известно [72], свободное движение материальной частицы. Здесь 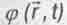- некая функция, характеризующая вероятность нахождения частицы в данной точке пространства в данный момент времени, как об этом догадался в 1927г. М.Борн.
r - радиус-вектор положения точки в пространстве,
k - волновой вектор, связанный с импульсом частицы соотношением

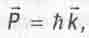(5.27)

со - циклическая частота волны, определяемая формулой Планка E = h , в которой Е- энергия частицы.
Разлагая экспоненциальный сомножитель в (5.26) по формуле Эйлера для комплексных чисел и пренебрегая мнимой частью разложения, как пренебрегают ею и при рассмотрении аналогичных уравнений для электромагнитных волн [73], получают:

(5.28)

Косинус здесь можно раскрыть в виде:

а скалярное произведение векторов - в виде:

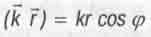(5.29)

где 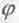- угол между векторами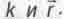
При совмещении начала координат с центром, вокруг которого обращается с циклической частотой Ω частица, скалярное произведение (5.29) для всех точек, лежащих на круговой орбите, по которой обращается частица, в моменты нахождения в этих точках частицы оказывается равным нулю (так как cos 90° = 0). Тогда выражение (5.28) упрощается в этих точках до .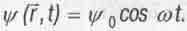
Если понимать 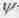- функцию как величину, характеризующую вероятность нахождения частицы в данной точке пространства-времени, то последнее выражение говорит, что эта вероятность максимальна в данных точках орбиты. Но она максимальна тут лишь в моменты, когда cos 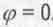. В остальные моменты времени 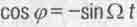здесь и надо говорить о суперпозиции двух гармонических процессов с частотами .
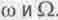Когда эти частоты близки, но не равны друг другу, должны наблюдаться биения, а когда отношение 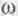/ оказывается целым числом, то возникает стоячая волна. Таковая наблюдается, например, при обращении электрона по стационарной орбите вокруг ядра в модели атома Бора.
До сих пор мы в данном разделе излагали давно известные азы квантовой механики. А теперь обратим внимание на то, что вдоль направления оси вращения cos 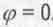в любые моменты времени t, a потому здесь

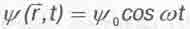(5.30)

в любые моменты времени.
Понятно, что на оси вращения так определенная 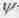- функция описывает уже отнюдь не вероятность нахождения частицы, а нечто иное, ибо частица, летящая по орбите вокруг оси вращения, никак не может оказаться на этой оси. Но на этой оси находится центр масс вращающейся системы. Значит, когда формула (5.30) указывает, что на оси вращения вероятность нахождения чего-то максимальна, то, оказывается, формулы не лгут! Но удивительно, что тут центр масс описывается как материальная точка, даже если в этом центре нет никакого материального тела, как в случае двойной звезды или позитрония.
А вот в сколь угодно близких к оси вращения ее окрестностях функция 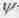(r t) уже является периодической (гармонической) функцией от расстояния г до центра вращения, 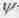- функция здесь попеременно принимает то положительные, то отрицательные значения, так как cos 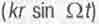здесь изменяется с ростом r периодически в пределах от +А до -А, где А - малое число, меньшее единицы. А это значит, что при вращении аксиально симметричного тела вокруг его оси симметрии - 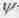- функции, задаваемые диаметрально противоположными частями тела, суммируясь здесь с противоположными знаками, будут давать в результате нуль.
Возможно ли, чтобы вдоль оси вращения вероятность нахождения здесь центра масс вращающейся системы тел была равна единице, а в сколь угодно близкой к ней окрестности становилась нулевой? Общие принципы квантовой механики указывают, что нет, вероятность должна спадать постепенно по мере удаления от оси вращения. Значит, где-то в наши выкладки вкралась ошибка.
И вот тут-то нам поможет теория движения. Из нее следует, как было убедительно показано в разделах 5.1 и 5.2, что вращательное движение - это мнимое движение, и тангенциальная скорость Vr как и импульс вращательного движения Рr должны описываться мнимыми числами. Тогда, в соответствии с (5.27), и волновой вектор k частицы, движущейся по круговой орбите, должен быть мнимым.
А если так, то при круговом движении частицы мы вместо (5.28) получаем несколько другую формулу для волн де Бройля:

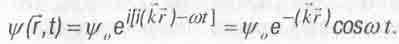(5.31)

Эта формула опять описывает стоячую волну, но отличается наличием сомножителя 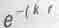обуславливающего экспоненциальное затухание волны с увеличением расстояния r от центра вращения. При этом затухание в разных направлениях происходит по-разному. В плоскости орбиты оно минимально вдоль направления от
центра вращения к частице (при таком направлении векторы 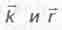взаимно перпендикулярны), и формула (5.31) здесь превращается в (5.30).
И вдоль оси вращения функция 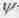(r,t) по-прежнему описывается формулой (5.30) и не затухает с расстоянием r. В этом все пока совпадает с выводами, полученными из общепринятой квантовой теории.
Различие же проявляется уже в ближайшей окрестности от оси вращения. Здесь cos (kr sin t) по-прежнему изменяется в пределах от +А до -А, но теперь этот косинус является уже не сомножителем произведения, а стоит в показателе степени экспоненциального сомножителя выражения (5.31). Потому 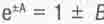где В -число, много меньшее единицы. Это означает, что теперь 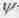- функции, задаваемые диаметрально противоположными частями вращающегося аксиально симметричного тела, в близких к оси вращения ее окрестностях уже не будут знакопеременными величинами, и их суммирование даст не нуль, а конечную величину. То есть вероятность нахождения здесь центра масс тела будет не нулевой, а хоть и очень малой, но конечной величиной.
Так с помощью теории движения мы достигаем естественного плавного и непрерывного распределения 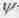-функции в пространстве возле оси вращения. Это еще раз показывает, что теория движения с ее представлением о вращательном движении как мнимом верна.
Вернемся к тому обстоятельству, что формула (5.31) описывает стоячую волну. Стоячая волна, как известно, предполагает отсутствие перетекания энергии через ее узловые точки. Но в промежутках между узловыми точками (в пучностях волны) происходит какое-то движение, превращение одного вида энергии в другой и обратно по гармоническому закону. Какое движение описывает формула (5.31) вне точек орбиты частицы? Колебательное движение квантовых осцилляторов физического вакуума? Или виртуальных частиц какого-то поля? Но ясно, что формула (5.31) описывает какое-то поле.
Поскольку в этой формуле фигурирует греческая буква 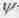, можно назвать это поле "пси-полем вращения". И получаем удивительное совпадение: пси-полем И. Шипов и А. Е. Акимов в своих публикациях иногда называют торсионное поле! Только у них приставка "пси" произошла от слова "психофизика", основы которой
они усматривают в торсионных полях.
Если наше выражение (5.31) описывает стоячую, а не бегущую волну, которую описывала формула де Бройля (5.26), то это означает, что пси-поле, описываемое нашей формулой (5.31), не распространяется в пространстве от точки к точке, а возникает во всех его точках, можно сказать, мгновенно в момент появления источника
токого поля. Это опять же совпадает с выводами Шилова и Акимова о торсионных полях. А мгновенность распространения поля предполагает, в соответствии с теорией тахионов [15] и рассмотрения тахионов с позиций теории движения в [9], отсутствие переноса таким полем энергии. И это тоже соответствует выводам Шилова о свойствах торсионных полей.
Кроме вышесказанного, из выкладок данного раздела, пожалуй, ничего нельзя сказать большего о скорости распространения торсионных полей, с которыми мы вынуждены отождествить так определенное нами 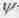-поле. Мы здесь даже не пытались составить для него волновое уравнение, в которое входила бы скорость распространения волн. Но отметим, что аналогом классического волнового уравнения Даламбера в квантовой механике для волн де Бройля является уравнение Шредингера, решением которого и служат уравнения плоской волны де Бройля (5.26). И давно подмечено, что уравнение Шредингера дает точные решения лишь в предположении мгновенности распространения описываемых им "волн вероятности" [74].
Чтобы теория окупала хотя бы стоимость той бумаги, на которой написана, она должна позволять легко рассчитывать что-то конкретное. Для этого преобразуем формулу (5.31) в вид, более пригодный для практических вычислений. Вспомнив, что 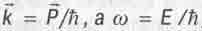перепишем выражение (5.31) в виде:

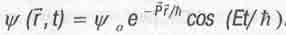(5.32)

Теперь здесь фигурируют не какие-то малопонятные величины 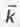и 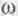, а вполне привычные для инженеров, легко осознаваемые и измеряемые ими энергия E и импульс P частицы.
Подставив далее в полученное выражение (5.32) значения импульса 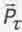и энергии E вращающейся системы из найденных выше формул (5.4) и (5.1), приведем выражение (5.32) к виду:

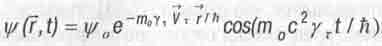(5.33)

(Здесь )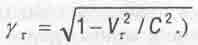
При технических и даже космических скоростях Vr величина у r с большой точностью близка к единице. Это облегчает расчеты для тел, имеющих технические массы и скорости вращения. Для них экспоненциальный сомножитель в (5.33) оказывается исчезающе малым для всех точек пространства кроме точек орбиты тела и оси его вращения или обращения с ее близкими окрестностями, где этот сомножитель равен единице или близок к ней. Это означает остронаправленность возникающего 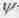- поля вращения (торсионного поля) вдоль оси вращения.
А вот для тел атомарных размеров ситуация существенно меняется. Например, для электрона, обращающегося в модели атома водорода со скоростью 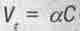(где - постоянная тонкой структуры) вокруг ядра по первой боровской орбите, имеющей радиус 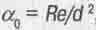, экспоненциальный сомножитель в (5.33) составит:

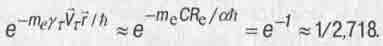
(Мы учли, что 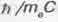- это комптоновская длина волны электрона, равная .)
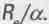Значит, в пределах размеров атомов 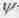-поля вращения во всех точках атома достаточно велики.
Но для нас важнее уяснить, что они столь же велики вдоль всей уходящей в бесконечность оси вращения и атома, и его ядра, как вдоль оси вращения (спина) любой элементарной частицы.
Для лучшего понимания того, что рассматриваемые поля являются полями вращения или торсионными полями, учтем, что если произведение 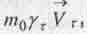, фигурирующее в показателе экспоненты в (5.33), домножить на вектор радиус орбиты 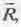то получим выражение для момента количества движения M. Тогда

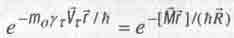(5.34)

Теперь в полученном выражении показатель экспоненты равен отношению момента количества движения М данного тела к элементарному (минимально возможному в природе) моменту количества движения h, умноженному на отношение радиуса - вектора r данной точки пространства к радиусу вращения 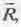. Только теперь в показателе экспоненты фигурирует не скалярное, а векторное произведение .
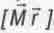В заключение этой главы отметим, что было бы очень любопытно и сравнительно несложно вычислить и градиент, и дивергенцию, и ротор от 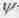- функции, определяемой выражением (5.31), и тем самым найти систему уравнений, описывающих торсионное поле по аналогии с системой уравнений Максвелла, описывающих электромагнитное поле. Но такая задача выходит за рамки данной книги.

Date: 2015-07-27; view: 865; Нарушение авторских прав